Вычисление суммы ряда и решение трансцендентного уравнения

М.А.И.

(Национальный Исследовательский Университет)

Лабораторная работа № 8

Вычисление суммы ряда и решение трансцендентного уравнения

Вариант № 23

Оформил: Антушев Юрий Дмитриевич

Проверил:

Москва 2011

Цель работы: Закрепление навыков работы со структурами повторения и выбора, а также знакомство с численными методами решения трансцендентных уравнений.

Задание 1.

Нахождение суммы ряда при помощи оператора for

S =[]; %пустой массив последовательности сумм

a=[]; %пустой массив последовательности членов ряда

s=0; %обнуление суммы

for N = 1:10

an = -(1+2/(3^(N+1)))*x^N;

s = s + an; %вычисление текущего значения суммы

a = [a an]; %формирование последовательности ряда

S = [S s]; %формирование последовательности сумм

end;

outstr = ['Сумма ряда = ', num2str(s)];

disp(outstr)

plot(a, '-b')

grid on

hold on

plot(S,'-r')

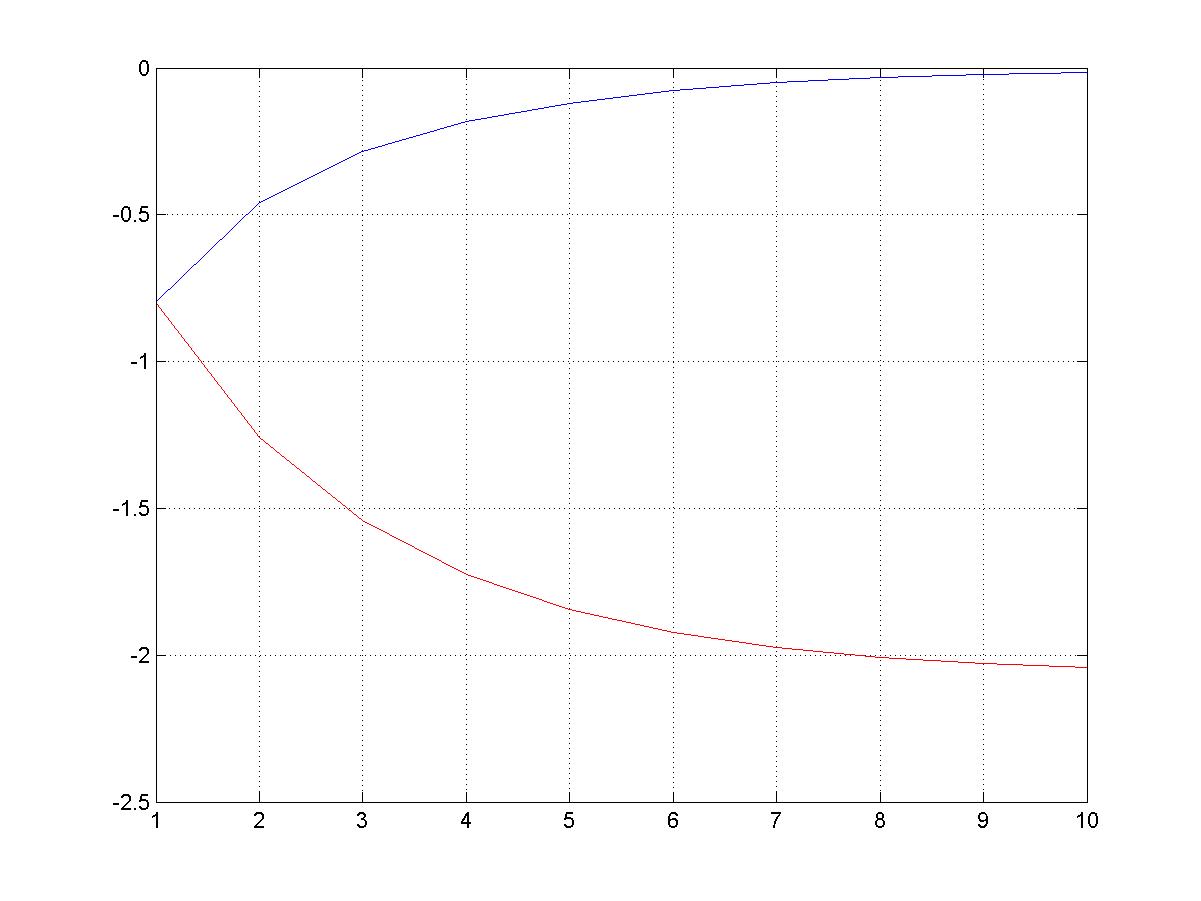
Нахождение суммы ряда при помощи оператора while

an=-(1+2/3); %значение первого члена ряда

a=[an] %массив последовательности членов ряда включает первый элемент

S = [an]; %массив последовательности сумм включает сумму ряда

%из одного элемента

s=an; %начальная сумма равна первому элементу

e = 1e-05; %допустимая погрешность вычислений

N=1;

while an > e %цикл повторяется, пока погрешность велика

N = N + 1;

an = -(1+2/(3^(N+1)))*x^N;

a = [a an]; %формирование последовательности ряда

s = s + an; %вычисление текущего значения суммы

S = [S s]; %формирование последовательности сумм

end;

%формирование строки вывода

outstr = ['Сумма ряда = ' num2str(s) '; Количество повторов = ' num2str(N)];

disp (outstr); %вывод результатов в командное окно

plot(a, '-b'), grid on, hold on, plot(S, '-r') %построение графиков

Задание 2. решение алгебраических или трансцендентных уравнений вида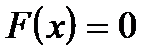

1.метод половинного деления (иначе - дихотомии, или бисекции).

e = 1e-04; %Устанавливаем допустимую погрешность

dx = 0.1; %шаг х при поиске интервала, содержащего корень

a = 0;

b = a;

while f(a)*f(b) > 0 %Определяем интервал, на котором

b = b + dx; % функция F(x) меняет знак

end;

a = b - dx;

x = (a+b)/2; % Первое приближение корня -

% середина найденного интервала

I = 1; % Счетчик итераций устанавливаем в "1"

X=[x]; % Формирование массивов для графиков

Y=[f(x)];

while abs(f(x)) > e

if f(x) * f(a) < 0 %Если функция имеет разные знаки

%на концах отрезка,

b = x; %сдвигаем правую границу

else

a = x; % иначе сдвигаем левую границу

end;

x = (a+b)/2; %и вычисляем следующее приближение

I = I + 1; %увеличиваем количество итераций на 1

X = [X x];

Y = [Y f(x)];

end;

Str = ['Значение корня: ' num2str(x) '; Количество итераций: ' num2str(I)];

disp(Str)

figure %Построение двух графиков в одном графическом окне

subplot(2, 1, 1);

plot(X, '-r'), grid on

subplot(2, 1, 2);

plot(Y, '-b'), grid on

В данном примере для корректной реализации необходимо создать еще один файл – файл-функцию, который имеет следующий вид:

function [ y ] = f (x)

y = 2*x*sin(x)-cos(x);

Имя функции «f», файл, в котором она находится, имеет имя «f.m», входным параметром является значение абсциссы «x», выходным – значение ординаты «y». Программа по ходу выполнения несколько раз обращается к функции, когда необходимо проверить знаки на концах интервала.

Результаты вычислений посредством метода половинного деления таковы:

Значение корня: 0.65327; Количество итераций: 11

На следующих графиках проиллюстрирован процесс сходимости решения (верхний график – сходимость значения корня, нижний – сходимость значения функции к нулю).

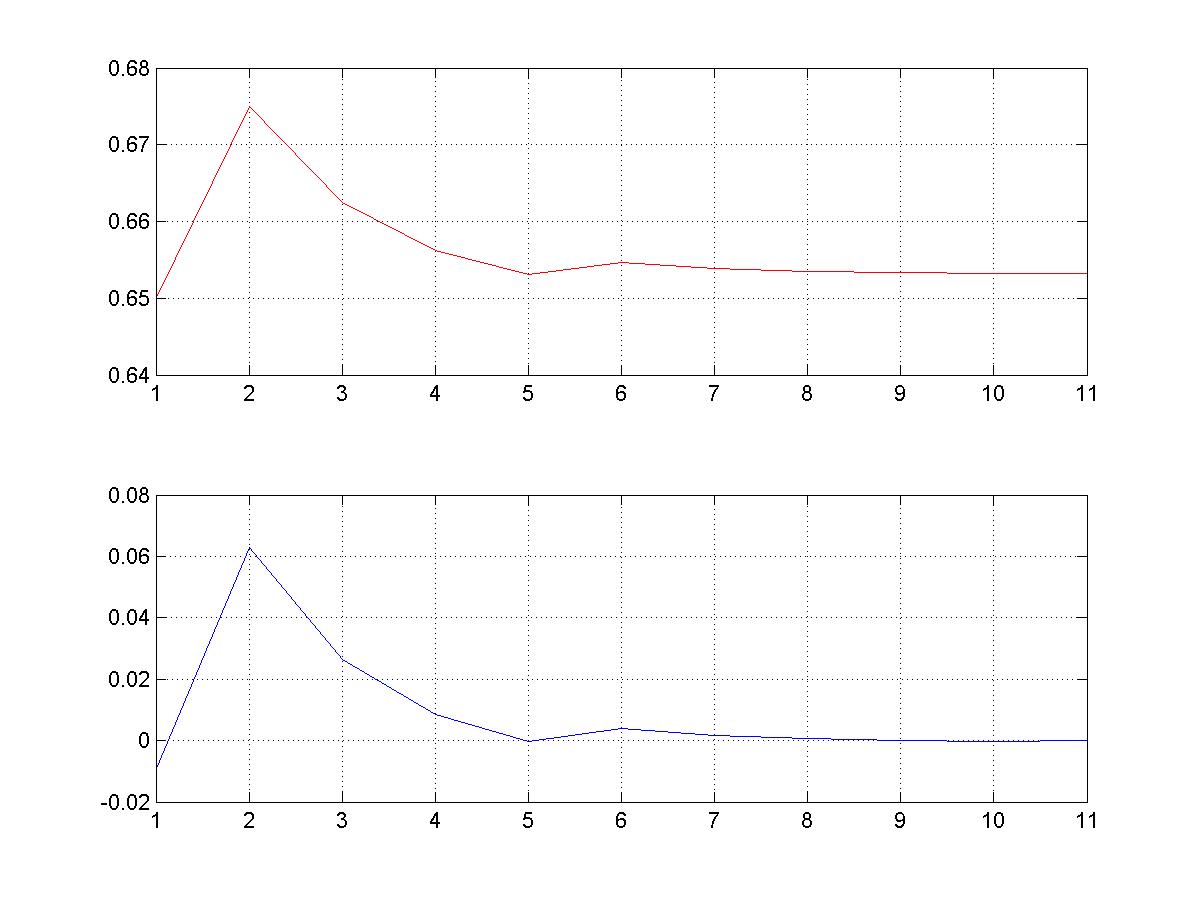
2. метод Ньютона

2*x*sin(x)-cos(x)=0

% Решение уравнения методом Ньютона

% F(x)=0

% F(x)=2*x*sin(x)-cos(x);

% F'(x)=3*sin(x)+2*x*cos(x);

% В данном примере ищется положительный корень

% Первое приближение = 0

e = 1e-08; %допустимая погрешность

x_k = 0.2; %задаем значение первого приближения

I = 0; %счетчик итераций I устанавливаем в ноль

delta = x_k;

D = [ delta ];

while abs(delta) > e %начало цикла итераций

xk_plus_1 = x_k - fun(x_k) / fun1(x_k); %следующее приближение

delta = xk_plus_1 - x_k; %текущая погрешность

D = [ D delta ];

x_k = xk_plus_1; %переприсваиваем приближения, чтобы перейти к следующему

I = I+1;

end;

Str = ['Значение корня: ' num2str(x_k) ];

disp(Str)

Str = ['Точность: ' num2str(delta) ];

disp(Str)

Str = ['Количество итераций: ' num2str(I) ];

disp(Str)

plot(D)

Из текста видно, что для решения необходимы две функци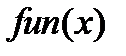и: и 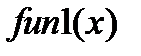(еще раз напомним, что имена файлов этих функций должны совпадать с именами самих функций). Указанные функции имеют вид:

function [ y ] = fun (x)

y = 2*x*sin(x)-cos(x);

и

function [ y1 ] = fun1(x)

y1 = 3*sin(x)+2*x*cos(x);

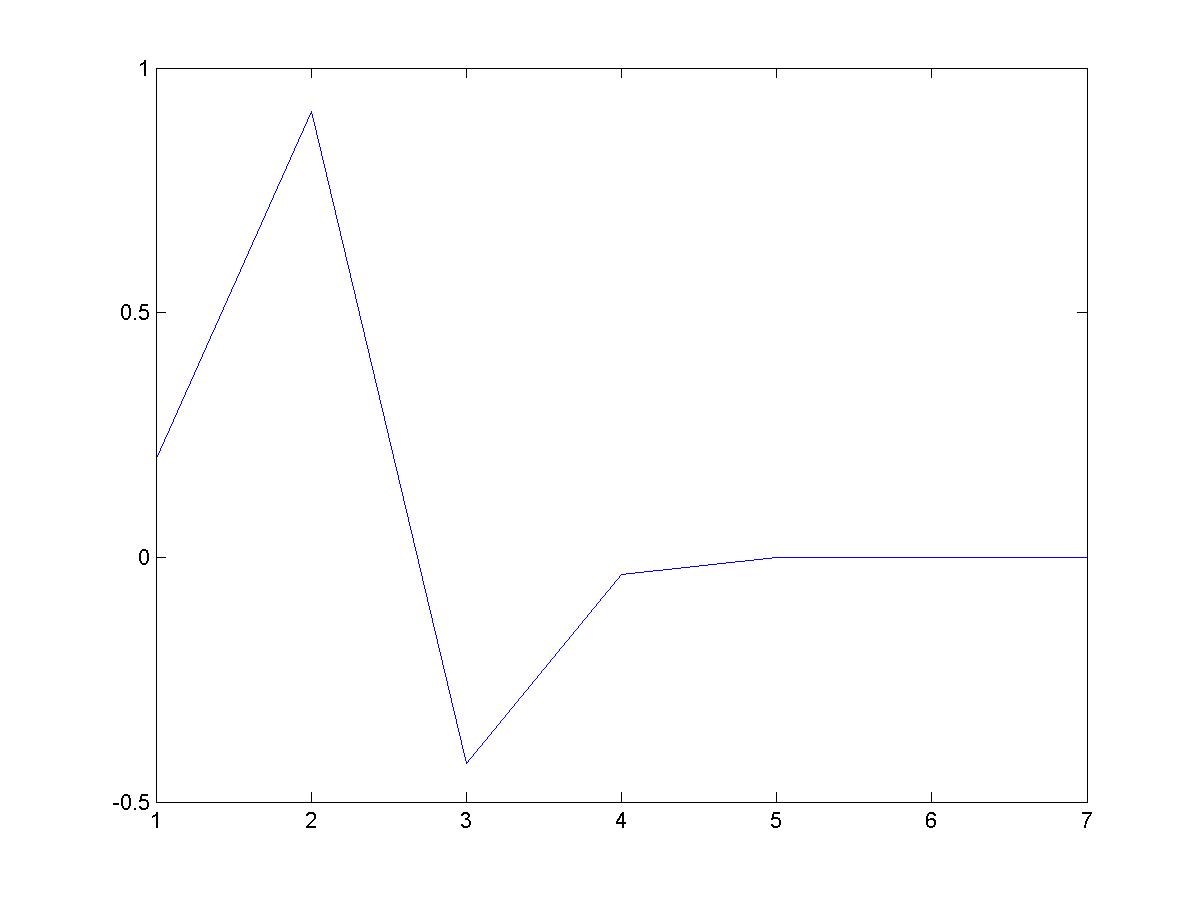
Результат выполнения программы таков:

Значение корня: 0.65327

Точность: -3.7748e-014

Количество итераций: 6

На следующем графике представлено изменение текущей погрешности вычисления корня (видно, что погрешность быстро убывает и уже с третьего приближения практически равна нулю):

3. метод простых итераций.

e = 1e-04; %допустимая погрешность

xk = 0.1; %задаем значение первого приближения

I = 0; %счетчик итераций I устанавливаем в ноль

delta = xk;

while abs(delta) > e %начало цикла итераций

xk_plus_1 = cos(xk)/(2*sin(xk)); %следующее приближение

delta = xk_plus_1 - xk; %текущая погрешность

xk = xk_plus_1; %перейти к следующему приближению

I = I+1;

end;

Str = ['Значение корня: ' num2str(xk) ];

disp(Str)

Str = ['Точность: ' num2str(delta) ];

disp(Str)

Str = ['Количество итераций: ' num2str(I) ];

disp(Str)

При заданном в качестве первого приближения значении 0.1 будут получены следующие результаты (требуемая точность установлена 10^-4):

Значение корня: 0.65331

Точность: 6.0298e-005

Количество итераций: 1018

4. метод секущих

% с использованием аналитического представления функции F(x) и ее производной

syms x; % объявляется символьная (аналитическая) переменная

% определяется аналитическое описание функции F(x)

f = 2*x*sin(x)-cos(x);

f1 = diff(f); % определяется производная функции F'(x)

% функция Matlab diff определяет производную (в данном случае – первую)

% по умолчанию функция Matlab diff определяет производную

% для определения второй производной и производных высших порядков

% в обращении к функции diff необходимо указать порядок производной,

% например, diff(f, 2) – для определения производной

ezplot(f), grid on, pause % строится график функции для визуального

% определения первого приближения корня.

% Функция pause используется для того, чтобы прервать выполнение программы

% для возможности визуальной фиксации приближенного значения корня и

% определения первого приближения по графику функции.

% Lля продолжения работы программы необходимо, не закрывая графического

% окна, нажать на клавишу Enter

err = 1e-04; % задается допустимая погрешность вычисления корня

delta = x0; % текущая погрешность вначале равна допустимой погрешности

X = [ x0 ]; % формируется вектор последовательных приближений

% корня к его конечному значению

n = 1; % номер первого приближения

N = [ n ]; % формируется вектор номеров приближений корня

% организуется цикл определения последовательных приближений корня

% методом Ньютона

while abs(delta) > err % повторять вычисления пока текущая погрешность

% больше допустимой

x1 = x0 - subs(f, x, x0) / subs(f1, x, x0); % Вычисляется следующее

% приближение корня.

% Функция SUBS используется для вычисления значения по аналитической формуле

% подстановкой в неё значения текущего приближения х0 вместо аналитической

% переменной х

delta = x1 - x0; % вычисляется текущая погрешность вычислений

x0 = x1; % следующее приближение становится текущим

X = [X x1]; % в вектор Х добавляется следующее приближение

n = n+1; % номер следующего приближения

N = [N n]; % в вектор N добавляется номер следующего приближения

end;

str_out = 'x = '; % формируется строка вывода результатов вычисления корня

res = num2str(x1);

str_out = strcat(str_out, ' ', res);

disp(str_out); % строка вывода отображается в командном окне

plot(N, X, 'Linewidth', 3, 'Color', [1 0 0]), grid on % строится график

Следующие графики иллюстрируют результаты выполнения программы.

На первом рисунке представлен график функции, из которого видно, что значение корня лежит между значениями 0 и 1. Это дает возможность в качестве первого приближения взять, например, значение, равное 0.2, которое вводится с клавиатуры во время диалога.

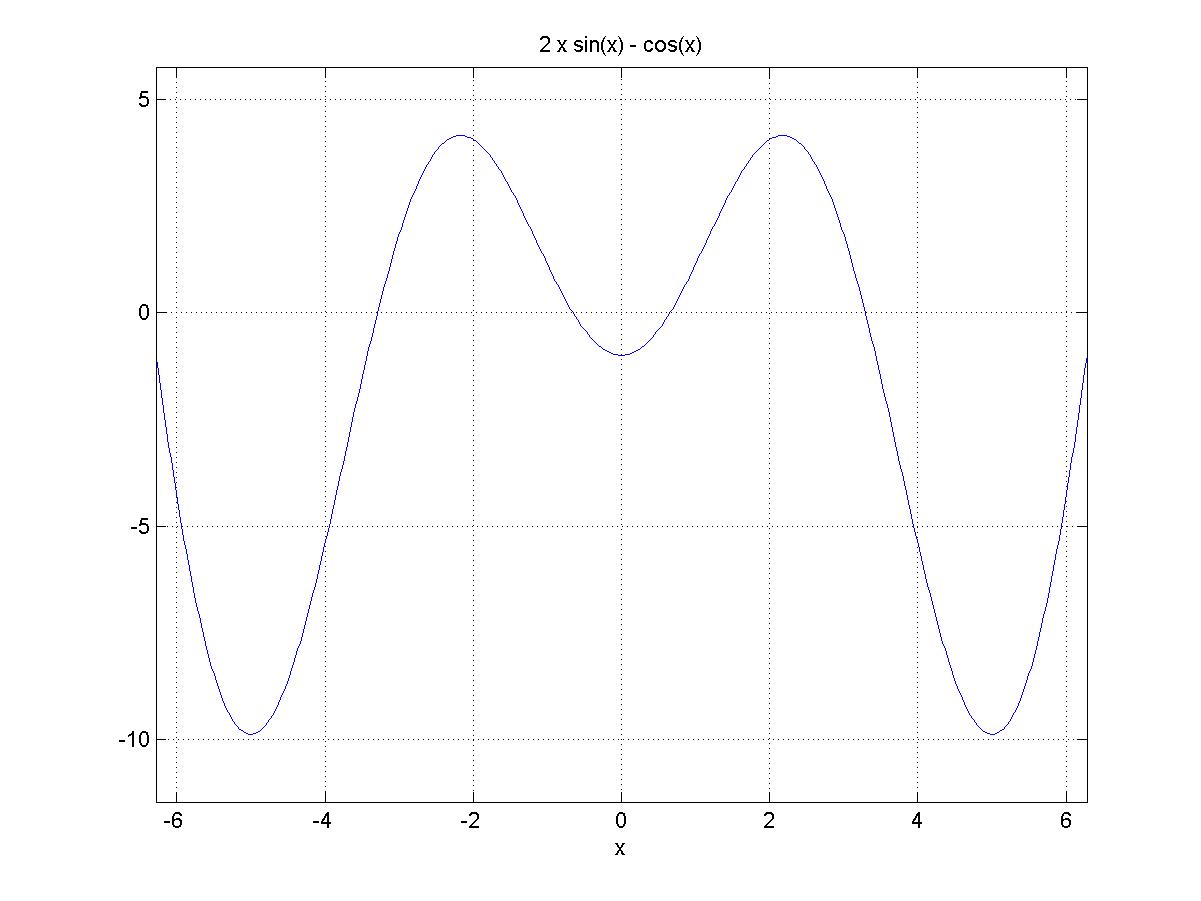
На втором рисунке показано изменение приближенного значения корня в процессе последовательных итераций. Видно, что значение корня стабилизируется после восьмой итерации. Это значение корня равно 0.6533

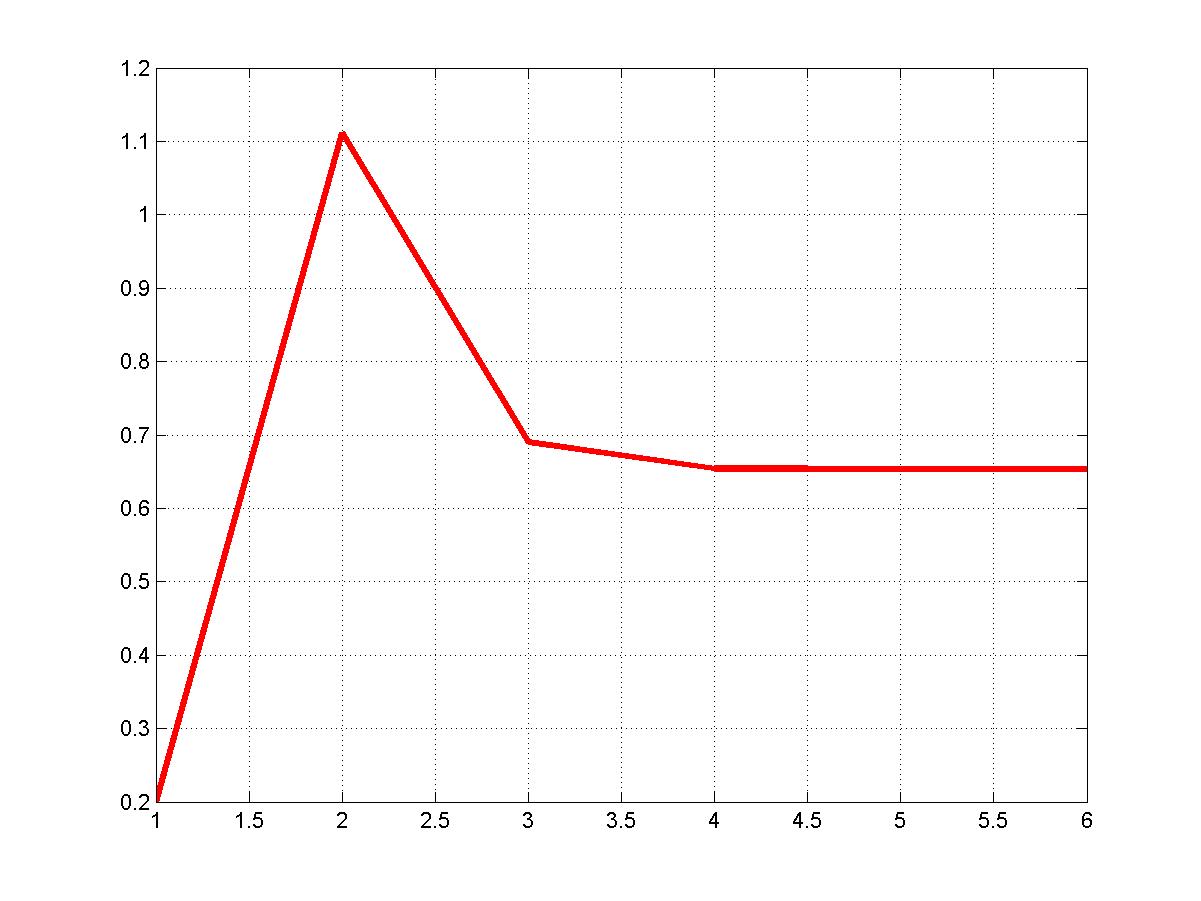
x =0.65327

5. Использование функции fzero для получения корня трансцендентного уравнения.

В заключение отметим, что в составе MatLab имеется функция fzero, позволяющая найти численно корень уравнения при условии, что задано его первое приближение. Для решения приведенного выше уравнения достаточно выполнить команду:

>> x0=1;

>> x=fzero('fun', x0)

и получить результат:

>> x =0.6533

Параметры функции очевидны из примера. Если имеется файл функции (в данном случае fun.m), то при помощи команды fplot можно построить график функции (например, чтобы проиллюстрировать решение уравнения). Команда построения графика выглядит так:

>> fplot('fun', [-6 6]);

а результат ее показан на следующем рисунке:

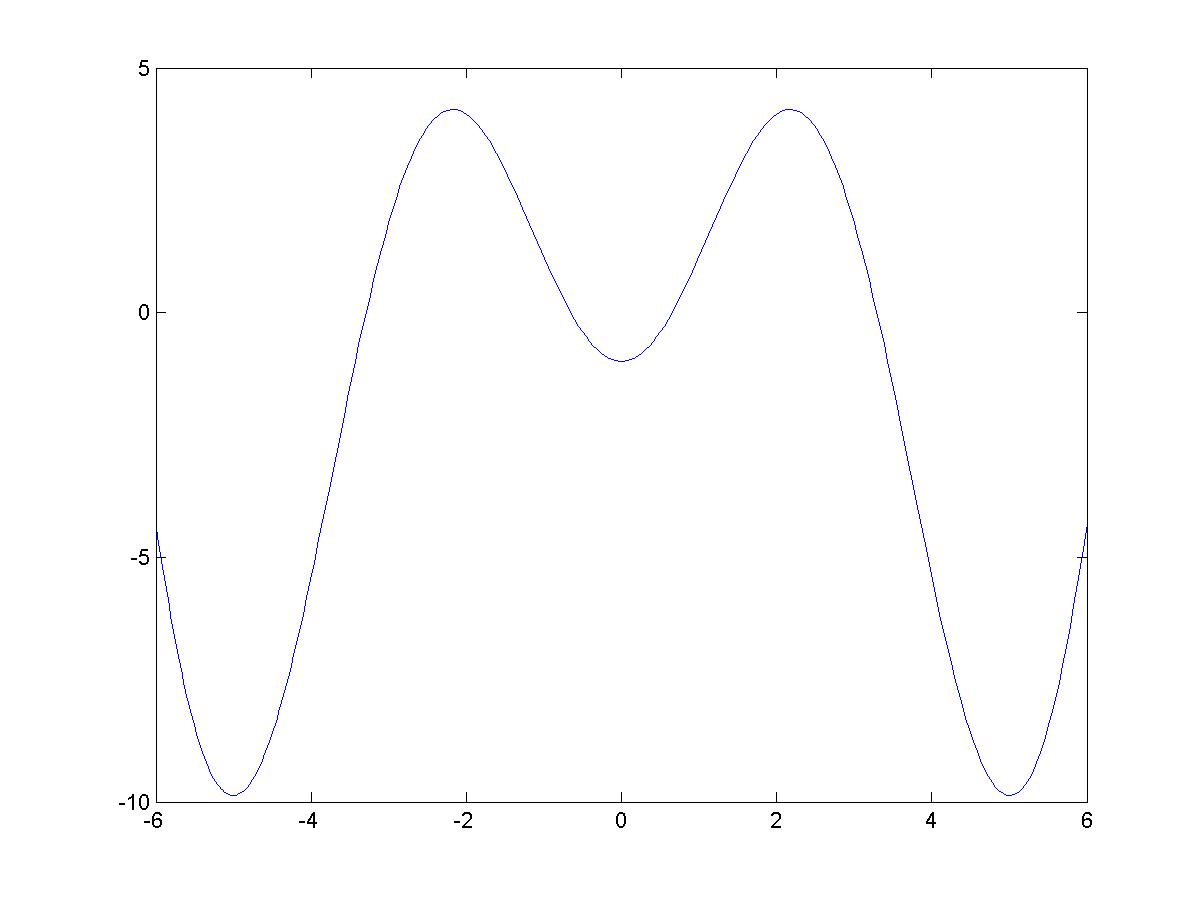
Вывод: я познакомился с трансцендентными уравнениями, посмотрел с помощью каких методов их решать и выяснил,что методов всего 5,а именно:

· метод последовательных приближений (простых итераций);

· метод Ньютона;

· модифицированный метод Ньютона;

· метод секущих;

· метод половинного деления (иначе - дихотомии, или бисекции).

Узнал в чем они схожи: при решении каждым из них происходит последовательное, шаг за шагом, уточнение значения корня от первоначального грубого приближения (или двух пер­во­на­чальных, как в методе секущих).

Отличия:

1. В методе простых итераций приближения организуются по правилу:

x_k+1= f(x_k), где k = 0, 1, 2, 3,...,

причем задается начальное (нулевое) приближение x₀. При известном начальном приближении определяется первое приближение, затем второе, третье и т.д. до тех пор, пока не будет достигнута требуемая точность (т.е. разность между двумя последовательными приближениями не станет пренебрежимо малой).

2. Алгоритм метода Ньютона строится исходя из представления функции F(x) в окрестности некоторой точки x* (предполагаемого корня уравнения), принадлежащей отрезку [a, b], в следующем виде:

F(x_k+1) = F(x_k) + (x_k+1 - x_k)* F ^¢(x_k) (5)

Исходя из равенства F(x)=0 и в соответствии с (5) (k+1) -e приближение определяется по правилу:

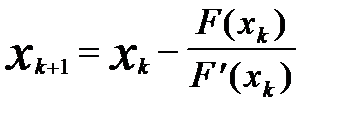, k=0,1,2,... (6)

Метод Ньютона иначе называется методом касательных (рис.2), поскольку для того, чтобы найти (k+1) -e приближение надо через точку x_k провести вертикальную прямую до пересечения с кривой F(x), затем провести касательную до пересечения с осью абсцисс (точка x _k+1), из точки x_k+1 - вновь вертикальную прямую до пересечения с F(x) и т.д.

3.