По закону сохранения энергии сумма кинетической и потенциальной энергии постоянна.
Вычислим гравитационную энергию шарообразного тела. Имеем шар радиуса R и массой M. Энергия гравитационного поля численно равна работе, которую необходимо затратить, чтобы частицы шара развести на бесконечное расстояние друг от друга.
Для упрощения примем, что шар однородный, его плотность 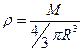 .
.
Сначала рассмотрим энергию твердого шарового ядра с радиусом r и окружающего его шарового слоя, толщина которого dr.
Масса центрального шара 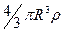 , масса слоя
, масса слоя 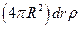 . Работа удаления шарового слоя толщиной dr равна потенциальной энергии шарового слоя в гравитационном поле, созданном всеми внутренними слоями (т.е. шаровым ядром радиуса r):
. Работа удаления шарового слоя толщиной dr равна потенциальной энергии шарового слоя в гравитационном поле, созданном всеми внутренними слоями (т.е. шаровым ядром радиуса r):
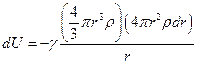 (2)
(2)
Гравитационная энергия шара радиуса R выразится
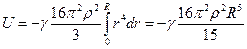 .
.
Так как 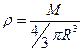 , то
, то
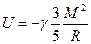 (3).
(3).
Эта энергия, которая связана с гравитационным взаимодействием частиц шара. Собственная энергия Солнца:

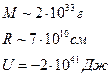
Вставка
Вычислим напряженность гравитационного поля внутри и вне шара радиуса R, заполненного веществом с постоянной объемной плотностью.
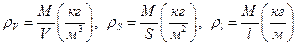
- Определим напряженность (g) гравитационного поля вне шара.
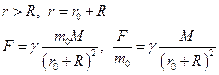
Если 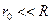 , то
, то 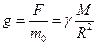 .
.
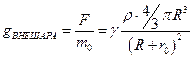 - с увеличением расстояния от центра шара напряженность убывает, и создается массой всего шара радиуса R.
- с увеличением расстояния от центра шара напряженность убывает, и создается массой всего шара радиуса R.
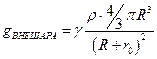
Напряженность внутри шара.
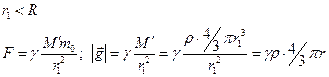 - напряженность внутри шара возрастает и создается только веществом шара, заключенным в сфере радиуса r1. То есть, на гравитационное поле не влияет вещество, расположенное вне вспомогательной сферы.
- напряженность внутри шара возрастает и создается только веществом шара, заключенным в сфере радиуса r1. То есть, на гравитационное поле не влияет вещество, расположенное вне вспомогательной сферы.
 2015-10-22
2015-10-22 4794
4794

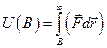 .
.