2015-02-04
2121
В настоящее время под гравитационным полем понимают поле тяготения, в котором все тела вне зависимости от их массы движутся в нем одинаковым образом. На основании закона всемирного тяготения Ньютона любые два тела притягиваются друг к другу с силой, которая направлена по линии, их соединяющей, прямо пропорциональной массам обоих тел и обратно пропорциональной квадрату расстояния между ними
,
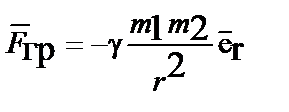где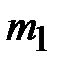 
, 
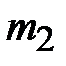– массы тяготеющих тел, g–постоянная тяготения Кавендиша.
Согласно общей теории относительности гравитация представляет собой просто геометрию пустого пространства и времени. Гравитация – это искривленное пространство – время. Понятие об ускорении заменено искривлением пространства. Электромагнетизм в ней – всего лишь часть гравитационного поля, действующая в пятом дополнительном измерении пространства, которое мы не в состоянии наглядно представить.
Исходя из такого определения электромагнетизма и гравитации, можно предположить существование глубокой связи между ними. Действительно, между электромагнитным и гравитационным полями, исходя из сравнения их основных законов, много общего. Так, силы в поле тяготения и электростатическом поле определяются аналогичными законами всемирного тяготения Ньютона и Кулона
|
|
|
; 
,
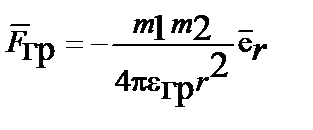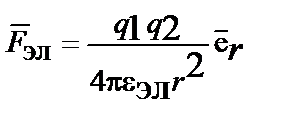где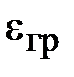 
=1/4pg – гравитационная проницаемость поля ускорений среды.
На основании второго закона Ньютона сила, действующая на тело, равна произведению массы тела на создаваемое этой силой ускорение, причем направления силы и ускорения совпадают, или ускорение равно отношению силы, деленной на массу тела. По аналогии с электрическим полем в гравитационном можно ввести понятие напряженности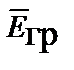 
поля ускорений как силы, с которой поле ускорений действует на точечное тело с единичной массой (инертной массой)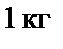 
; 
.
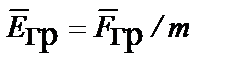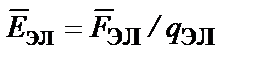Из закона сохранения массы гравитационный ток, по аналогии с электрическим, можно определить как количество массы (инертной массы), выходящее за некоторый промежуток времени через замкнутую поверхность S, ограничивающую объем V, равное величине уменьшения находящейся в объеме массы тела (инертной массы), за тот же промежуток времени:
; 
,
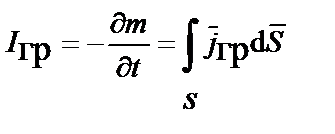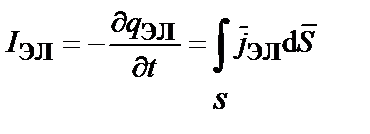где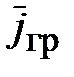 
– плотность гравитационного тока.
В дифференциальной форме закон сохранения массы (инертной массы), как и электрического заряда, представляется в виде уравнений непрерывности:
; 
,
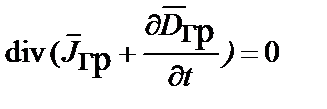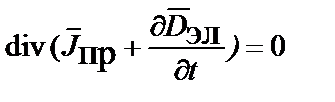где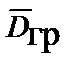 
– вектор индукции поля ускорений, равный произведению гравитационной проницаемости среды 
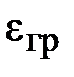на вектор напряженности поля ускорений:
= 
; 
= 
.
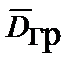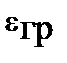
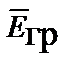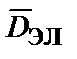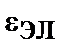
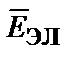Поток вектора индукции поля ускорений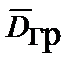 
через замкнутую поверхность S, по аналогии с теоремой Гаусса для электростатического поля, равен массе тела (инертной массе), находящейся внутри объема, ограниченного этой поверхностью:
|
|
|
; 
,
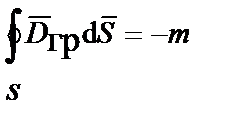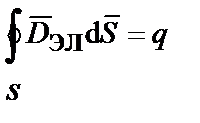или в дифференциальной форме:
; 
,
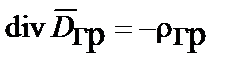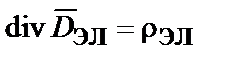где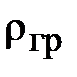 
– объемная плотность массы тела (инертной массы).
Последнее уравнение с учетом закона сохранения массы совпадает с известным в механике сплошных сред уравнением неразрывности в переменных Эйлера
.
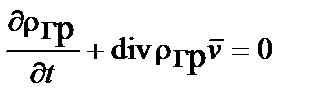Отрицательный знак перед массой тела в законах сохранения заряда учитывает притяжение тел в гравитации по сравнению с отталкиванием одноименных электрических зарядов в электростатике.
В статическом гравитационном поле, как и в электростатическом, можно ввести понятие скалярного гравитационного потенциала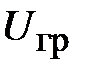 
:
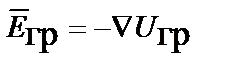или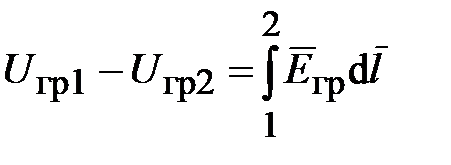 
,
где разность скалярных гравитационных потенциалов равна работе по перемещению единичной массы тела из одной точки в другую.
Так, например, при нормировании потенциала в бесконечно далекой точке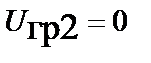 
, скалярный потенциал на поверхности Земли при ее массе 
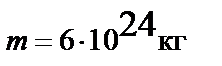равен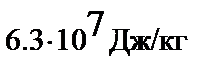 
, а напряженность поля ускорений 
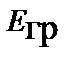= 9.8 Н/кг, и она притягивает тело массой в один килограмм к своей поверхности с силой в 9.8 Н.
Общее выражение для энергии статического гравитационного поля, по аналогии с электростатическим полем,
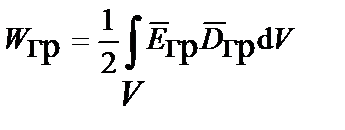
может, с учетом основного тождества
,
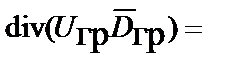
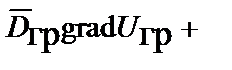
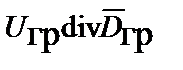преобразовано к виду:
.
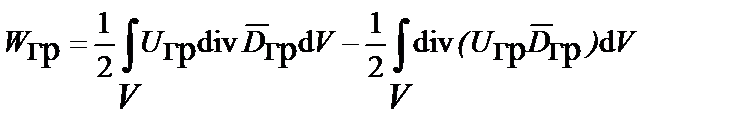После замены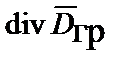 
удельной объёмной массой – 
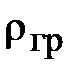, а во втором слагаемом объёмного интеграла – на поверхностный интеграл, получаем:
.
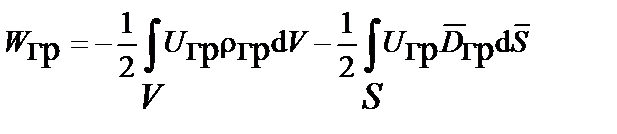Если масса сосредоточена в ограниченной области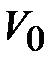 
, то при удалении поверхности S в бесконечность поверхностный интеграл исчезает, так как площадь этой поверхности увеличивается с расстоянием как 
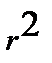, а произведение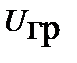 
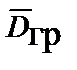при этом уменьшается как 
.
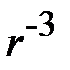Поэтому гравитационная энергия массы, находящейся в ограниченной области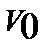 
, будет равна
.
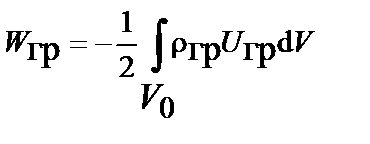Эта зависимость совпадает с выражением для энергии электростатического поля при условии взаимной замены скалярных потенциалов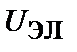 
, 
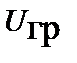и объемных плотностей 
, – 
.
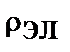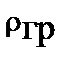Итак, подобие законов всемирного тяготения и Кулона, сохранения массы и заряда, а также уравнений непрерывности позволяет говорить об аналогии гравитационного поля ускорений с электрическим полем.
Кроме напряженности электрического поля, движущиеся или изменяющиеся во времени электрические заряды создают вокруг себя магнитное поле. Можно предположить, что при движении или изменении во времени масс (инертных масс), вокруг них образуется второе гравитационное поле, напряженность которого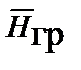 
определяется из закона, аналогичного закону Био – Савара
,
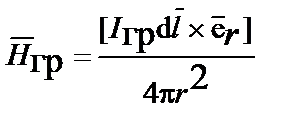где 
– элемент гравитационного тока.
Из размерности вектора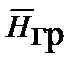 
, 
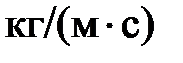, видно, что он характеризует импульсное поле. Как известно, произведение массы тела на его скорость называют в механике импульсом (или количеством движения) тела.
Импульс тела – величина векторная. Вектор напряженности импульсного гравитационного поля определяет значение импульса на единицу поверхности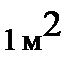 
.
Всеобщий закон сохранения импульса о постоянстве суммарного импульса системы при отсутствии внешних сил, даже если тела системы разрушаются, отражает то обстоятельство, что векторные линии импульсного поля, как и магнитного, всегда замкнуты, не имеют ни начала, ни конца.
Итак, вторым полем в гравитации может быть импульсное поле, совместно с полем ускорений образующее единое гравитационное поле.
Уравнения Максвелла для гравитационного поля. Cвязь между импульсным полем и полем ускорений, исходя из рассмотренной аналогии между гравитацией и электромагнетизмом, а также исходя из единства природы и ее закономерностей, может быть определена из уравнений, аналогичных уравнениям Максвелла (табл. 4.1) и трех уравнений связи или вещественных уравнений [4]:
= 
; 
; 
= 
,
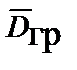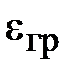
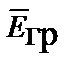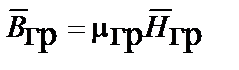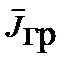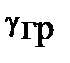
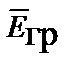где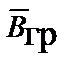 
– вектор индукции импульсного поля, 
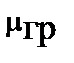– проницаемость импульсного поля среды, 
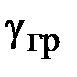– удельная гравитационная проводимость.
|
|
|
Для эфира, исходя из равенства скоростей электромагнитных и гравитационных волн инертных масс электромагнитного поля в нём и величины постоянной тяготения Кавендиша, гравитационные проницаемости равны:
, 
.
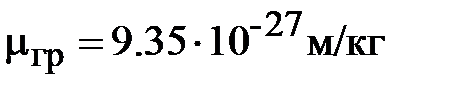Таблица 4.1
| Интегральная форма уравнений | Дифференциальная форма уравнений |
 
|  
|
| 
|
| 
|
| 
|
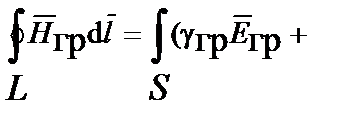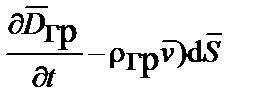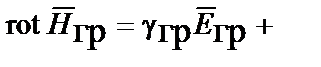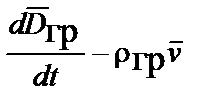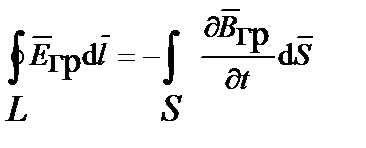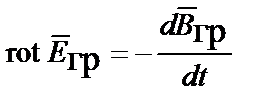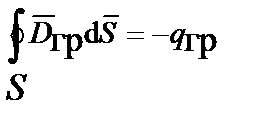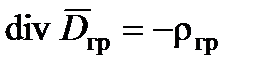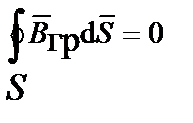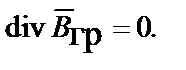Для движущихся со скоростью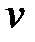 
тел, обладающих гравитационными зарядами (массами, определяемыми из закона Ньютона) гравитационные проницаемости сред находятся из выражения, аналогичного фазовой скорости эквивалентной волны
.
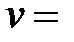
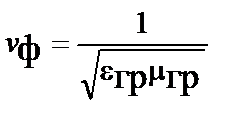Волновые уравнения. Для определения уравнения, которому удовлетворяет каждый вектор поля в пространстве вне гравитационных источников, применим операцию ротации к I и II уравнениям Максвелла для гравитационного поля:
; 
.
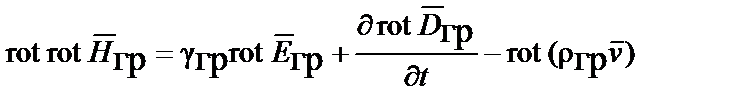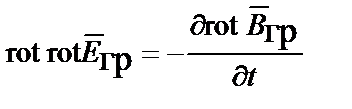После подстановки значений роторов векторов и замены двойного ротора разностью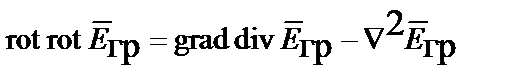 
находим
;
.
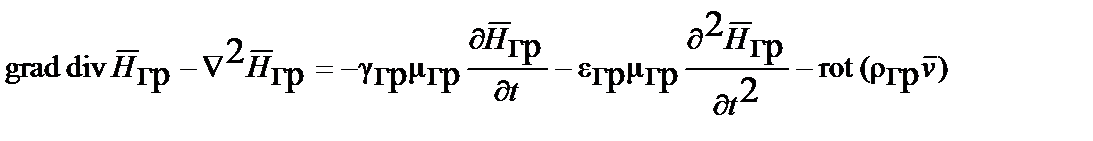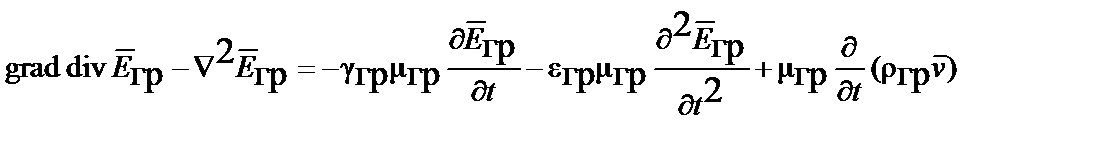С учётом III и IV уравнений Максвелла получаем обобщенные неоднородные векторные волновые уравнения:
;
.
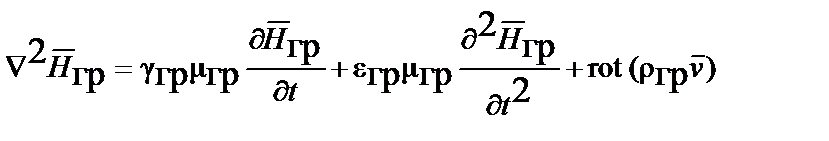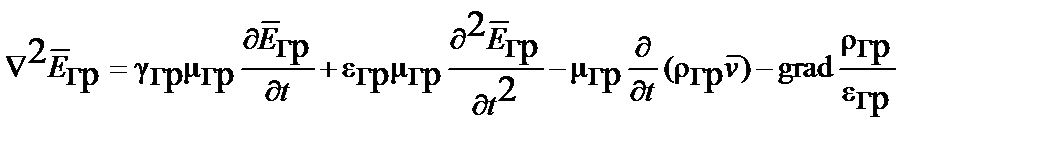Итак, в однородном пространстве вне источников, когда сторонние токи, возбуждающие поле, находятся за пределами анализируемой части пространства, векторы напряженности поля ускорений и импульсного поля удовлетворяют обобщенным неоднородным векторным волновым уравнениям.
Волновые дифференциальные уравнения второго порядка в частных производных в гравитации описывают распространение колебаний в среде. Они наряду с пространственными производными второго порядка содержат вторые производные по времени.
Волновые уравнения для стационарного, независимого от времени гравитационного поля,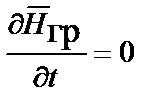 
или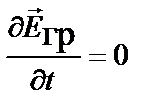 
, переходят в уравнения Пуассона, описывающие потенциальные поля:
; 
.
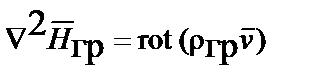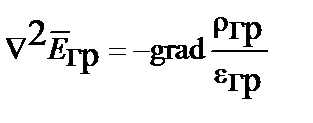Волновые уравнения записаны в общей форме, пригодной для любой системы координат. Дляих решения следует раскрыть оператор Лапласа в конкретной системе координат и заменить векторные уравнения системой скалярных уравнений. Наиболее простой вид оператор Лапласа имеет в декартовой системе координат.
Любая краевая задача теории гравитационного поля сводится к определению в пространстве и времени векторов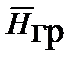 
и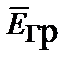 
, удовлетворяющих волновым уравнениям при заданных начальных и граничных условиях.
|
|
|
Векторные и скалярные потенциалы. Векторные и скалярные потенциалы вводят для упрощения решения полевых задач. Вместо решения двух неоднородных волновых уравнений для векторов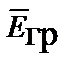 
и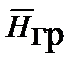 
решается одно уравнение для векторного потенциала поля ускорений 
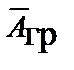или импульсного векторного потенциала 
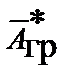, связанных следующими соотношениями с векторами гравитационного поля:
, 
;
, 
,
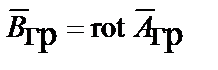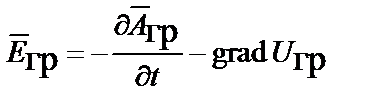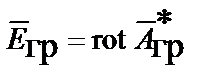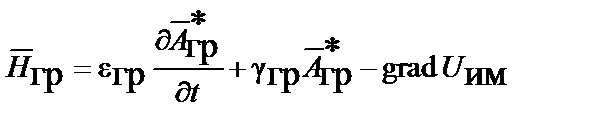где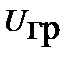 
– скалярный потенциал поля ускорений, 
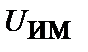– скалярный потенциал импульсного поля.
Векторные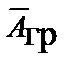 
, 
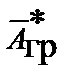и скалярные потенциалы 
, 
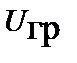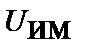удовлетворяют неоднородным волновым уравнениям:
;
;
;
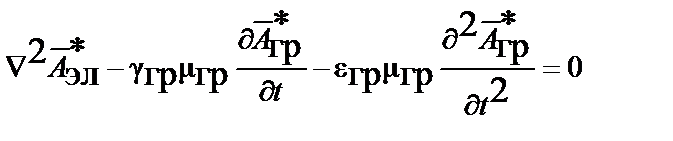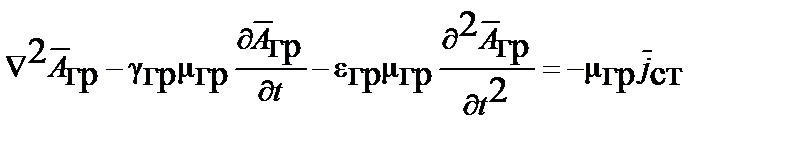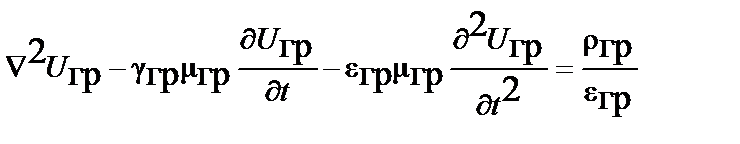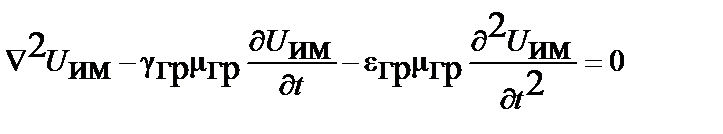
при выполнении следующих равенств, аналогичных условиям Лоренца в электромагнитном поле:
; 
.
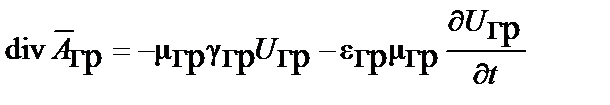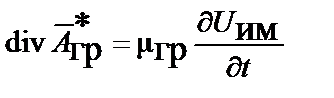Для доказательства этого следует, например, вместо вектора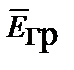 
подставить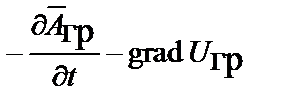 
в правую часть I уравнения Максвелла, вместо вектора 
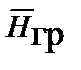подставить 
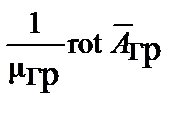в левую часть этого же уравнения; воспользоваться тождеством 
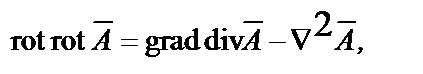условием Лоренца 
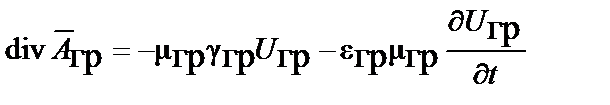и получить искомое волновое уравнение для векторного потенциала:
.
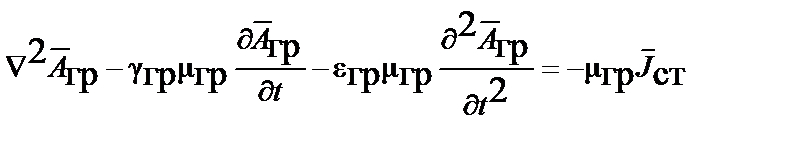Волновое уравнение для скалярного импульсного потенциала получается после дифференцирования условия Лоренца по времени, подстановки в него значения производной от векторного потенциала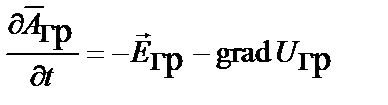 
, замены дивергенции от вектора напряженности поля ускорений правой частью III уравнения Максвелла, делённой на проницаемость среды, и представления оператора Лапласа вместо дивергенции градиента.
Для стационарных полей волновые уравнения переходят в уравнения Пуассона:
; 
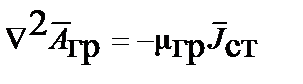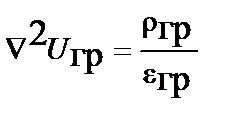
и уравнения Лапласа:
; 
.
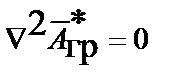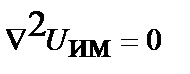Векторное уравнение Пуассона в декартовой системе координат распадается на три скалярных уравнения.
Учитывая, что фундаментальное решение уравнения Пуассона для скалярного потенциала в однородных средах имеет вид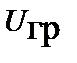 
= 
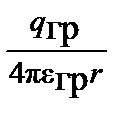, то в общем случае точечного, объемного, поверхностного и линейного распределения гравитационных зарядов (масс) результирующий скалярный потенциал будет определяться алгебраической суммой их скалярных потенциалов. Поэтому частное решение уравнения Пуассона равно алгебраической сумме скалярных потенциалов отдельных, объёмных, поверхностных или линейных гравитационных зарядов
.
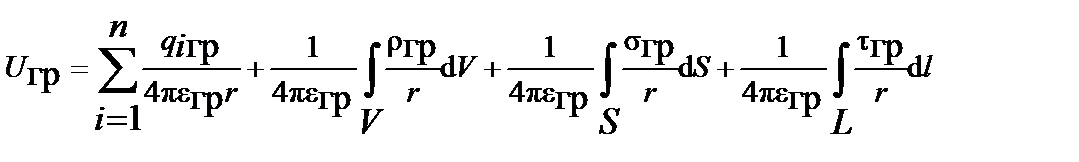Используя фундаментальное решение уравнения Пуассона относительно векторного потенциала поля ускорений, можно определить векторный потенциал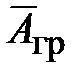 
,
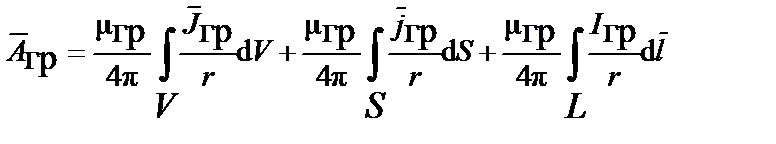где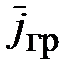 
– плотность тока, измеряемая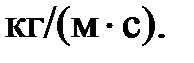 
Напряженность поля в некоторых задачах целесообразно определять, рассчитывая производные потенциала от расстояния аналитически:
; 
.
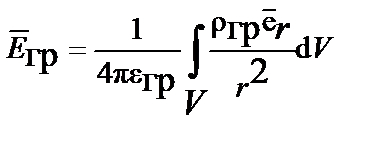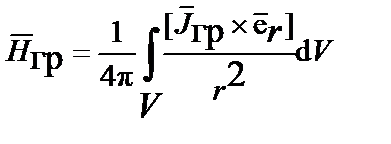Закон сохранения энергии. Энергия сторонних гравитационных токов в данном пространстве может накапливаться гравитационным полем, распространяться и преобразовываться в другие виды энергии.
Для определения баланса мощностей, как и в случае электромагнитного поля, дополним I уравнение Максвелла вектором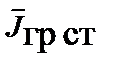 
плотности токов гравитационных сторонних сил и скалярно умножим его на вектор 
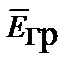, а II уравнение умножим на вектор 
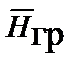, из второго произведения вычтем первое. Тогда, с учетом тождества
,
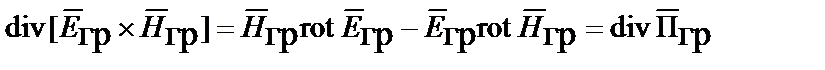получим уравнение Пойнтинга в дифференциальной форме для мгновенных векторов гравитационного поля в виде
,
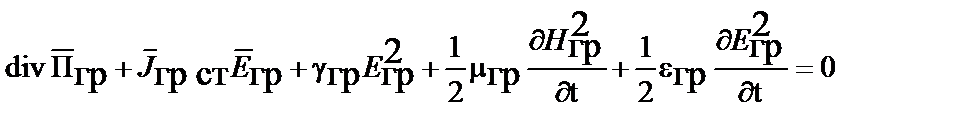где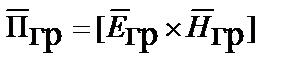 
– вектор Пойнтинга представляет поток мощности гравитационного поля, проходящий через 
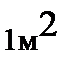поверхности; 
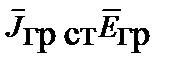– удельная мощность сторонних гравитационных сил; 
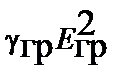– удельная мощность тепловых потерь; 
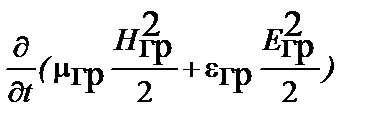–суммарная удельная мощность, запасенная полем ускорений и импульсным полем. Проинтегрируем уравнение Пойнтинга по объему. С учётом интеграла Остроградского – Гаусса получаем теорему Пойнтинга в интегральной форме для мгновенных значений векторов гравитационного поля
,
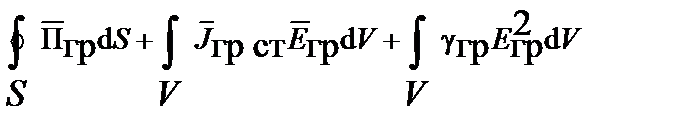
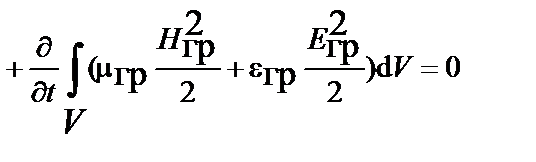где первый интеграл суммы – поток вектора плотности мощности гравитационного поля через замкнутую поверхность S, охватывающую объем V; второй интеграл – мощность источника сторонних токов в объеме V; третий интеграл – мощность тепловых потерь в объеме V; последний интеграл – мощность гравитационного поля, сосредоточенная в объеме V.
Сумма мощностей источников сторонних токов, тепловых потерь, поля ускорений и импульсного поля в объеме и потока мощности гравитационного поля, проходящего через поверхность S объема V, равна нулю, что позволяет рассматривать теорему Пойнтинга в качестве уравнений баланса мгновенных мощностей гравитационного поля в пространстве объема V, ограниченном поверхностью S.
Переменные во времени векторы напряженности поля ускорений и импульсного поля удовлетворяют волновым уравнениям, в комплексном виде уравнению Гельмгольца
; 
,
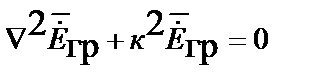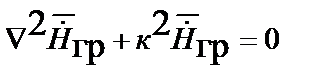где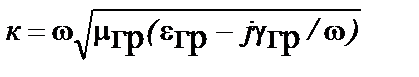 
– комплексное волновое число.
Итак, с введением второго векторного поля в гравитации появилась полная аналогия между электрическим полем и полем ускорений, между магнитным полем и импульсным полем, т.е. аналогия между гравитацией и электромагнетизмом. Гравитационное поле, исходя из данного анализа, подчиняется законам, подобным законам электромагнитного поля см. табл.4.2.
Законы гравитационного поля
Таблица 4.2
| Закон | Интегральная форма | Дифференциальная форма |
| Гравитационное статическое (импульсное статическое) поле | ||
| ЗаконНьютона |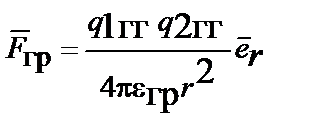 
| |
| ТеоремаГаусса |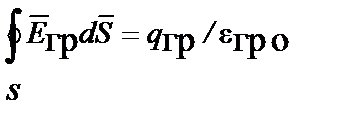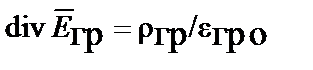 
| 
|
| Закон сохранения заряда |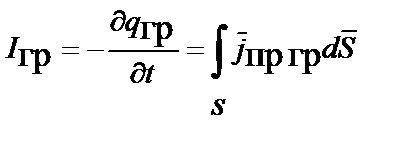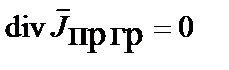 
| 
|
| Поле ускорений постоянного гравитационного тока в проводящих средах | ||
| Первый закон Кирхгофа |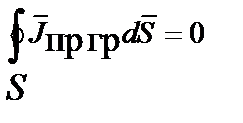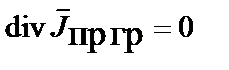 
| 
|
| Второй закон Кирхгофа |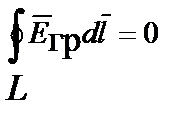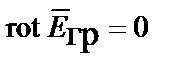 
| 
|
| Закон Ома для электрической цепи |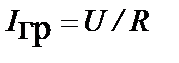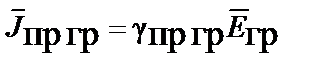
| 
|
| Закон Джоуля-Ленца |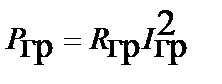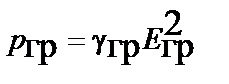 
| 
|
Окончание табл. 1.1
| Закон | Интегральная форма | Дифференциальная форма | |
| Импульсное поле постоянного гравитационного тока | |||
| Закон Ампера |  ,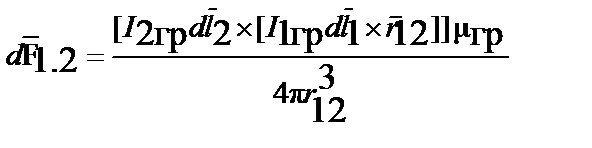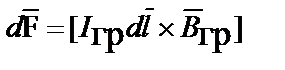 
| ||
| Закон Био – Савара |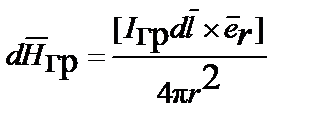 
| ||
| Закон Ома для магнитной цепи |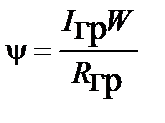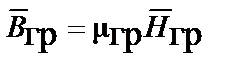 
| 
| |
| СилаЛоренца |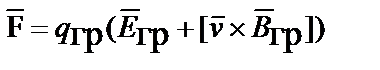 
| ||
| Закон полного тока |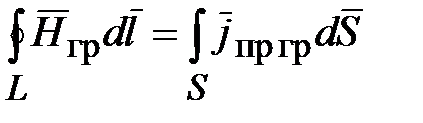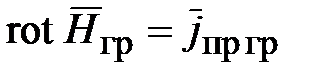 
| 
| |
| Переменное гравитационное поле | |||
| Обобщённый закон полного тока |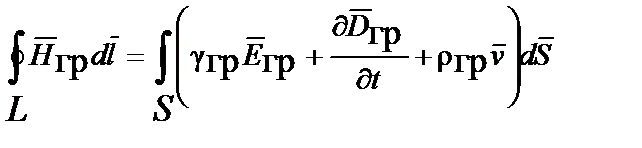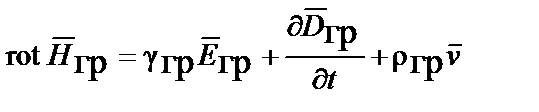 
| 
| |
| Закон Фарадея |  .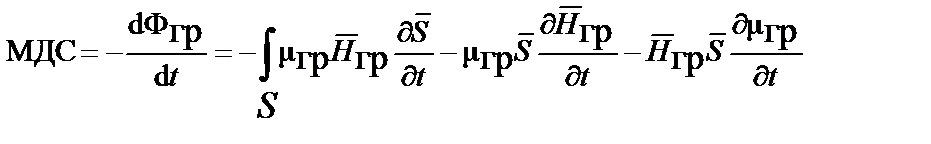
| ||
| Закон импульсной индукции |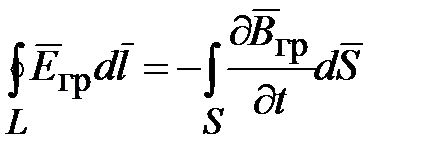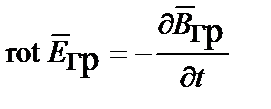 
| 
| |
В эфире гравитационные волны инертных масс электромагнитного поля распространяются в виде поперечных волн со скоростью света.
Гравитационным полем, как известно, обладаютвсе тела планеты. В состоянии относительного покоя тело имеет только одно статическое поле ускорений, при его движении вокруг и внутри тела возникает импульсное гравитационное поле, по направлению движения тела начинает распространяться, следовать с ним, поток мощности кинетической энергии. Этот поток находится внутри и вне тела. При торможении, в соответствии с законом сохранения энергии, он переходит в тепло.
Сила Лоренца в гравитации – результирующая суммарная сила поля ускорений и импульсного поля, действие которой испытывает движущийся гравитационный заряд в гравитационном поле. Траекторию перемещения гравитационного заряда (массой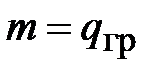 
) в гравитационном поле, как и в электромагнитном поле, находят из уравнения движения
,
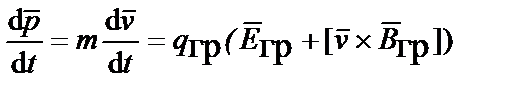связывающего изменение импульса p частицы во времени с силой Лоренца.
С учётом равенства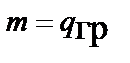 
уравнение движения частицы не зависит от её массы 
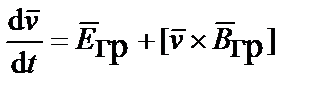, т.е. все тела вне зависимости от их массы движутся в гравитационном поле одинаковым образом.
Эта особенность гравитационного поля позволила [5] движение тел в нём заменить эквивалентными системами отсчета: равномерно ускоренной при постоянном внешнем гравитационном поле и неравномерно ускоренной при переменном внешнем гравитационном поле.
Уравнения Максвелла для гравитационного поля, как и для электромагнитного поля, могут быть получены и из принципа наименьшего действия [6]. Так действие можно представить в виде интеграла по времени из функции Лагранжа, определяющей энергии движущихся частиц, поля и взаимодействия частиц с полем. Для движущейся со скоростью v частицы, обладающей массой m или гравитационным зарядом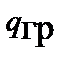 
, в скалярном статическом 
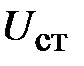и переменном гравитационном поле функция Лагранжа в объеме V равна следующей сумме энергий
.
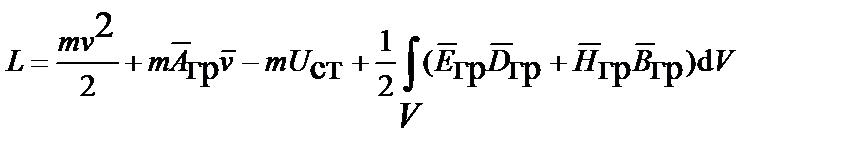Определим II и IV уравнения Максвелла для гравитационного поля варьированием в действии траекторией частицы в неизменном поле. Для этого производную по времени от частной производной функции Лагранжа по скорости представим в виде частной производной функции Лагранжа от расстояния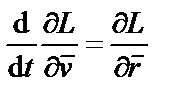 
.
Производная по времени от частной производной функции Лагранжа по скорости, после подстановки функции Лагранжа и дифференцирования по скорости, равна разности производных по времени
= 
,
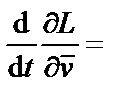
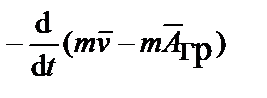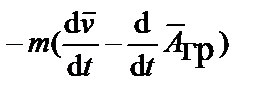а частная производная функции Лагранжа от расстояния – разности градиентов
= 
.
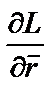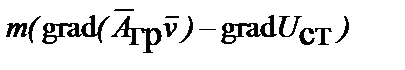В результате получаем равенство разностей производных по времени и градиентов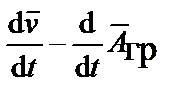 
= 
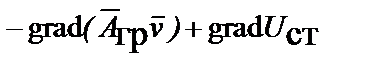. С учетом формул основных тождеств векторного анализа
; 
+ 
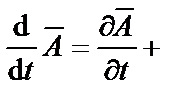
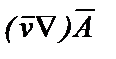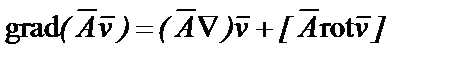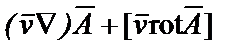
помня, что дифференцирование по r производится при постоянной скорости v, находим уравнение движения частицы в гравитационном поле
= 
,
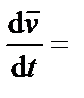
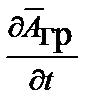
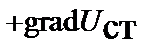
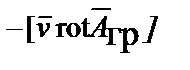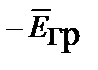
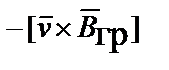где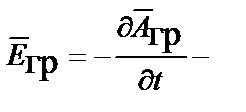 
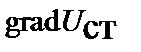, а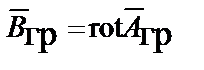 
.
Применив операции ротации к вектору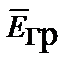 
и дивергенции к вектору 
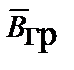, принимая во внимание, что ротор всякого градиента и дивергенция всякого ротора равны нулю, получаем II и IV уравнения Максвелла
; 
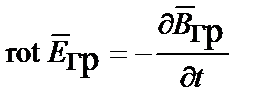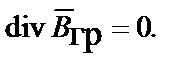
Определим III и I уравнения Максвелла для гравитационного поля варьированием в действии при заданном движении частиц.
Варьируем скалярным потенциалом
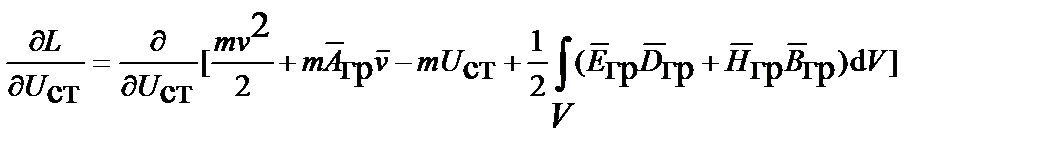
и, приравняв производную к нулю, получаем
.
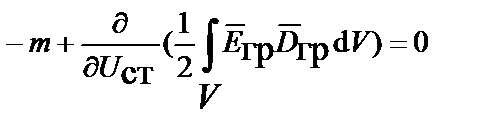Представляя заряд частиц в виде объёмного интеграла, а приращение потенциала через напряженность статического гравитационного поля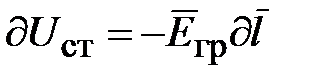 
, находим III уравнение Максвелла
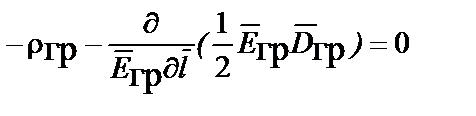, III. 
.
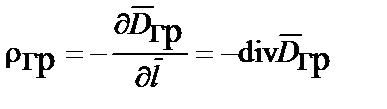Варьируем векторным потенциалом
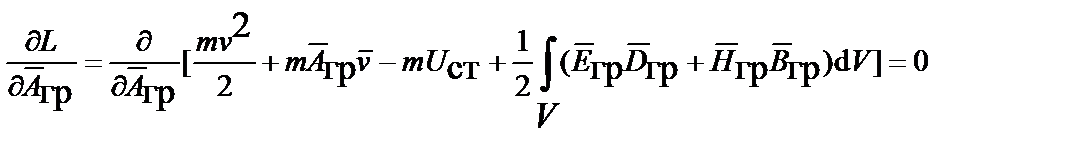
и с учетом,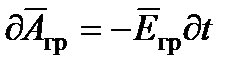 
,
; 
,
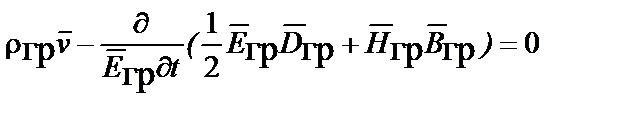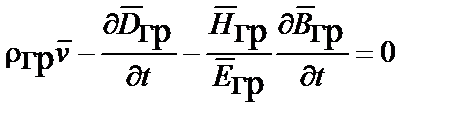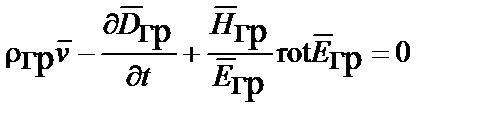принимая во внимание
;
,
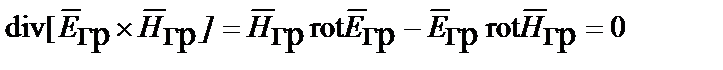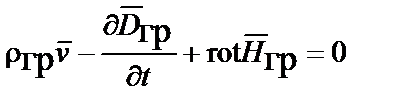находим I уравнение Максвелла
.
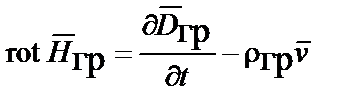Вывод уравнений для гравитационного взаимодействия, подобных уравнениям Максвелла, из принципа наименьшего действия подтверждает предположение их достоверности в описании гравитационных полей.
Граничные условия для векторов напряженности и индукции гравитационного поля. Уравнения Максвелла в дифференциальной форме, содержащие производные от составляющих векторов по координатам, теряют смысл в точках разрыва на границах раздела сред с различными проницаемостями поля ускорений, импульсов и удельными проводимостями. Поэтому при решении краевых задач используют граничные условия, определяющие поведение векторов поля на границе раздела сред.
Граничные условия определяют из уравнений Максвелла для гравитационного поля в интегральной форме. Предполагают, что граница раздела двух сред обладает некоторой малой толщиной (рис. 4.1), в пределах которой происходит непрерывный переход параметров верхней среды в параметры нижней среды. Такое же непрерывное изменение происходит и c векторами поля.
Пределы интегрирования в I и II уравнениях Максвелла по бесконечно малому замкнутому контуру abcd, разбивают на горизонтальные участки ab по верхней и cd нижней границам и на вертикальные участки bc и da промежуточного слоя. При стремлении толщины промежуточного слоя к нулю, т.е. осуществлении предельного перехода векторов с верхней среды в нижнюю среду, интегралы с пределами интегрирования на вертикальных участках bc и da бесконечно малы по величине.В результате интегралы в I и II уравнениях Максвелла равны сумме из двух скалярных произведений или разности произведений тангенциальных составляющих векторов на элемент пути, так как интегрирование по верхней границе противоположно направлению интегрирования по нижней границе
I.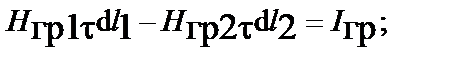 
II.
.
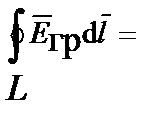
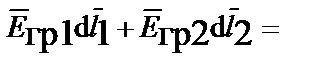
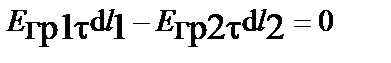Пределы интегрирования в III и IV уравнениях Максвелла по бесконечно малой замкнутой поверхности цилиндра разбивают на участки по его боковой поверхности и по его основаниям. При стремлении толщины промежуточного слоя к нулю, интегралы с пределами интегрирования по боковой поверхности бесконечно малы по величине. В результате интегралы в III и IV уравнениях Максвелла равны сумме из двух скалярных произведений или разности произведений нормальных составляющих векторов на элемент поверхности, так как интегрирование по верхнему основанию цилиндра противоположно направлению интегрирования по нижнему основанию цилиндра:
III.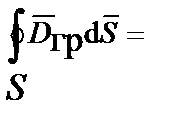 
;
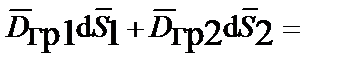
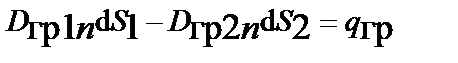IV.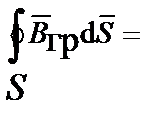 
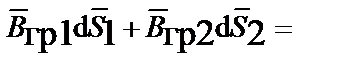
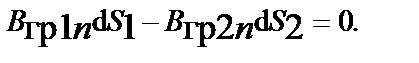
В результате из уравнений Максвелла в интегральной форме получают следующие граничные условия:
, 
;
, 
.
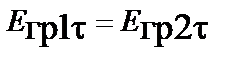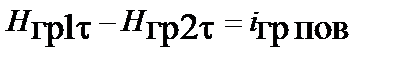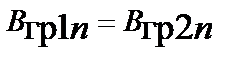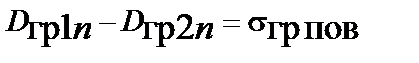При отсутствии на границе поверхностных токов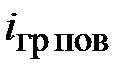 
= 0 тангенциальные составляющие векторов напряженности поля ускорений и импульсного поля непрерывны, а при отсутствии на границе поверхностных зарядов 
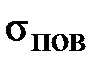= 0 непрерывны нормальные составляющие векторов индукции поля ускорений и импульсного поля.
