Механический коэффициент полезного действия (КПД)

Энергия, подводимая к механизму в виде работы движущих сил А_{дв.с .} и моментов за цикл установившегося движения, расходуется на совершение полезной работы А_{п.с .}, а также на совершение работы А_Fтр, связанной с преодолением сил трения в кинематических парах и сил сопротивления среды.

Рассмотрим установившееся движение. Приращение кинетической энергии равно нулю, т.е.

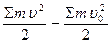= 0.

При этом работы сил инерции и сил тяжести равны нулю А_Ри = 0, А_G = 0. Тогда для установившегося движения работа движущих сил равна

А_дв.с.=А_п.с.+ А_Fтр.

Следовательно, за полный цикл установившегося движения работа всех движущих сил равна сумме работ сил производственных сопротивлений и непроизводственных сопротивлений (сил трения).

Механический коэффициент полезного действия η (КПД) – отношение работы сил производственных сопротивлений к работе всех движущих сил за время установившегося движения:

η = 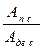. (3.61)

Как видно из формулы (3.61), КПД показывает, какая доля механической энергии, приведенной к машине, полезно расходуется на совершение той работы, для которой машина создана.

Отношение работы сил непроизводственных сопротивлений к работе движущих сил называется коэффициентом потерь:

ψ = 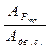. (3.62)

Механический коэффициент потерь показывает, какая доля механической энергии, подведенной к машине, превращается в конечном счете в теплоту и бесполезно теряется в окружающем пространстве.

Отсюда имеем связь между КПД и коэффициентом потерь

η =1- ψ.

Из этой формулы вытекает, что ни в одном механизме работа сил непроизводственных сопротивлений не может равняться нулю, поэтому КПД всегда меньше единице (η <1). Из этой же формулы следует, что КПД может равняться нулю, если А_дв.с=А_Fтр. Движение, при котором А_дв.с= А_Fтр называется холостым. КПД не может быть меньше нуля, т.к. для этого необходимо, чтобы А_дв.с<А_Fтр. Явление, при котором механизм находится в покое и при этом удовлетворяется условие А_дв.с<А_Fтр, называется явлением самоторможения механизма. Механизм, у которого η = 1, называется вечным двигателем.

Таким образом, коэффициент полезного действия находится в пределах

0 £ η < 1.

Рассмотрим определение КПД при различных способах соединения механизмов.

3.2.2.1. Определение КПД при последовательном соединении

Пусть имеется n последовательно соединенных между собой механизмов (рисунок 3.16).

А_дв.с. 1 А₁ 2 А₂ 3 А₃ А_n-1 n A_n

…

Рисунок 3.16 - Схема последовательно соединенных механизмов

Первый механизм приводится в движение движущими силами, которые совершают работу А_дв.с. Так как полезная работа каждого предыдущего механизма, затрачиваемая на производственные сопротивления, является работой движущих сил для каждого последующего механизма, то КПД первого механизма будет равняться:

η₁ =А₁ / А_{дв.с ..}

Для второго механизма КПД равняется:

η₂ =А₂ / А_{1 .}

И, наконец, для n-го механизма КПД будет иметь вид:

η_n =А_n / А_n-1

Общий коэффициент полезного действия равен:

η_1n =А_n / А_дв.с.

Величина общего КПД может быть получена, если перемножить КПД каждого отдельного механизма, а именно:

η_1n= η₁ η₂ η₃ …η_n = .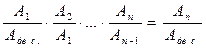

Следовательно, общий механический коэффициент полезного действия последовательно соединенных механизмов равняется произведению механических коэффициентов полезного действия отдельных механизмов, составляющих одну общую систему:

η_1n= η₁ η₂ η₃ …η_n. (3.63)

3.2.2.2 Определение КПД при смешанном соединении

На практике соединение механизмов оказывается более сложным. Чаще последовательное соединение сочетается с параллельным. Такое соединение называется смешанным. Рассмотрим пример сложного соединения (рисунок 3.17).

Поток энергии от механизма 2 распределяется по двум направлениям. В свою очередь от механизма 3^¢¢ поток энергии распределяется также по двум направлениям. Общая работа сил производственных сопротивлений равна:

А_п.с.= A^¢_n+ A^¢¢_n+ A^¢¢¢_n.

Общий КПД всей системы будет равен:

η =А_п.с / А_дв.с= (A^¢_n+ A^¢¢_n+ A^¢¢¢_n)/ А_{дв.с .} (3.64)

Чтобы определить общий КПД, нужно выделить потоки энергии, в которых механизмы соединены последовательно, и рассчитать КПД каждого потока. На рисунке 3.17 показаны сплошной линией I-I, штриховой линией II-II и штрих- пунктирной линией III-III три потока энергии от общего источника.

I I

1 2 3^¢ n^¢

А_дв.с. А₁ А^¢₂ А^¢₃ … А^¢_n-1 A^¢_n

II А^¢¢₂ II

А^¢¢₃ 4^¢¢ А^¢¢₄ А^¢¢_n-1 n^¢¢ A^¢¢_n

III 3^¢¢ …

А^¢¢¢₃ III

А^¢¢¢₄ 5^¢¢¢ А^¢¢¢₅ А^¢¢¢_n-1 n^¢¢¢ A^¢¢¢_n

4^¢¢¢ …

Рисунок 3.17 - Схема смешанного соединения механизмов

КПД каждого потока будет равен:

η^¢_1n= η₁ η₂ η^¢₃ …η^¢_n = A^¢_n / А^¢_дв.с

η^¢¢_1n= η₁ η₂ η^¢¢₃ …η^¢¢_n = A^¢¢_n / А^¢¢_дв.с

η^¢¢¢_1n= η₁ η₂ η^¢¢¢₃ …η^¢¢¢_n = A^¢¢¢_n / А^¢¢¢_дв.с.

Выразим работу движущих сил из этих уравнений:

А^¢_дв.с=A^¢_n / η^¢_1n

А^¢¢_дв.с=A^¢¢_n / η^¢¢_1n (3.65)

А^¢¢¢_дв.с=A^¢¢¢_n / η^¢¢¢_1n

Общая работа движущих сил всей системы будет равна сумме

А_дв.с = А^¢_дв.с + А^¢¢_дв.с + А^¢¢¢_дв.с.

Или А_дв.с =(A^¢_n / η^¢_1n)+(A^¢¢_n / η^¢¢_1n)+(A^¢¢¢_n / η^¢¢¢_1n).

Подставим это выражение в формулу (3.64), получим уравнение коэффициента полезного действия для смешанного соединения

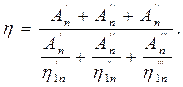(3.66)

Для параллельно соединенных механизмов методика определения КПД аналогична предыдущему случаю.