2015-10-22
2425
О сравнительном значении характеристик вариационного ряда говорят в тех случаях, когда рассматривают два или более ряда чисел. Сравнение числа с числом всегда очевидно и не подлежит обработке каким-либо методом. Сравнение же ряда чисел с другим рядом невозможно провести без дополнительной математической обработки.
Пользуясь характеристиками вариационных рядов, сравнению подлежат средние арифметические между собой и факторы рассеивания между собой. В этом случае сравнение двух рядов чисел сводится к сравнению двух чисел, что всегда очевидно.
Естественно, такое сравнение можно проводить не только для двух, но и для большего числа рядов в зависимости от запросов практики.
Рассмотрим примеры на сравнение рядов.
Пример 12. Зафиксированы результаты в толкании ядра у двух спортсменов. Результаты первого (хi—в метрах) приведены и обработаны в табл. 28, результаты второго — в табл. 29.
Сравнение проводим по средним арифметическим между собой и коэффициентом вариации между собой.
|
|
|
Таблица 28
| xi | ni | xini | xi- 
| (xi- )2
| (xi- )2ni
| ||||||
| 12,50 | 25,00 | --1,00 | 1,00 | 2,00 | |||||||
| 13,00 | 39,00 | —0,50 | 0,25 | 0,75 | |||||||
| 13,60 | 108,80 | +0.10 | 0,01 | 0,08 | |||||||
| 13,80 | 55,20 | +0.20 | 0,04 | 0,16 | |||||||
| 14,00 | 28,00 | +0,50 | 0,25 | 0,50 | |||||||
| 14,20 | 14,20 | +0,70 | 0,49 | 0,49 | |||||||
| n=20 | 270,20 | 3,98 | |||||||||
Таблица 29
| xi | ni | xini | xi-
| (xi- )2
| (xi- )2ni
| ||||||
| 12,50 | 12,50 | -0,90 | 0,81 | 0,81 | |||||||
| 13,00 | 91,00 | —0,40 | 0,16 | 1,12 | |||||||
| 13,60 | 81,60 | +0.20 | 0,04 | 0,24 | |||||||
| 13,80 | 41,40 | +0.40 | 0,16 | 0,48 | |||||||
| 14,00 | 28,00 | +0,60 | 0,36 | 0,72 | |||||||
| 14,20 | 14,20 | +0,80 | 0,64 | 0,64 | |||||||
| n=20 | 268,70 | 4,01 | |||||||||
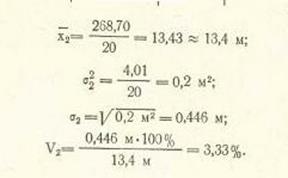
При сравнении исходных данных видно, что оба спортсмена показывали одни и те же результаты, но разное число раз. В таких случаях сравнение без математической обработки невозможно, особенно если показаний много.
Определив характеристики ряда в обоих случаях, сравниваем их между собой. Оказывается, что оба спортсмена показывают почти одинаковую стабильность в результатах (V1=3,3%, V2=3,33%), т. е. первый дает стабильные показания, имеющие среднюю арифметическую 1=13,5 м, а второй—при средней 2=13,4 м. Таким образом, сравниваем их средние и делаем вывод, что первый спортсмен показывает, в среднем, более высокий результат в толкании ядра.
Пример 13. Две группы школьников выполняют броски в баскетбольное кольцо с пяти попыток. Результаты попаданий первой группы школьников приведены в табл. 30, второй—в табл. 31. Значения хi (в бросках) — количество попаданий с пяти попыток. Обе таблицы обработаны с целью определения характеристик вариационных рядов.
Таблица 30
| xi | ni | xini | xi-
| (xi- )2
| (xi- )2ni
|
| —2 | |||||
| -1 | |||||
| +1 | |||||
| +2 | |||||
| +3 | |||||
| n=30 |
|
|
|
Таблица 31
| xi | ni | xini | xi-
| (xi- )2
| (xi- )2ni
| |
| —3 | ||||||
| -2 | ||||||
| —2 | ||||||
| +1 | ||||||
| +2 | ||||||
Сравнивая между собой средние арифметические ( 1=2 броска и 2=3 броска), можно было бы говорить о преимуществах второй группы перед первой. Об этом же говорят значения коэффициентов вариации (V1=79,6% и V2 = 53,5%). Однако, значение коэффициентов вариации в обоих случаях очень велико. Все это говорит об очень низкой квалификации в данном упражнении у обеих групп школьников. Так что вряд ли есть смысл говорить о преимуществах какой-либо из групп при забрасывании мяча в кольцо.
Пример 14. Школьник совершает прыжки вверх из глубокого приседа толчком обеих ног, прогнувшись. Зафиксировано количество прыжков, которое он мог выполнить подряд в 12 лет (табл. 32; хi—в прыжках), и количество прыжков, совершаемое им в 13 лет (табл. 33).
Ряды обработаны обычным способом.
Таблица 32
| xi | ni | xini | xi-
| (xi- )2
| (xi- )2ni
|
| n=10 | —2 —1 +1 +2 |
Таблица 33
| xi | ni | xini | xi-
| (xi- )2
| (xi- )2ni
|
| —2 | |||||
| +1 | |||||
| +2 | |||||
| п=10 |
Одинаковый в обоих случаях коэффициент вариации (V1=3,5% и V2=3,5%) свидетельствует о стабильных показаниях школьника в этом упражнении. При такой стабильности он незначительно улучшил результаты за год ( 1=33 прыжка; 2=35 прыжков).
По-видимому, было бы интересно проследить его дальнейшее развитие при помощи этого или какого-либо другого упражнения.
Пример 15. В спорте к числу самых распространенных задач относится сравнение результатов каких-либо измерений у контрольной и экспериментальной групп с целью выявления эффективности предлагаемой методики.
Две группы прыгунов в длину показали такие результаты (xi—прыжки в длину в метрах): табл. 34—контрольная группа, табл. 35 — экспериментальная группа.
Результаты обработаны обычным способом.
Таблица 34
| xi | ni | xini | xi-
| (xi- )2
| (xi- )2ni
|
| 4,60 | 9,20 | —0,30 | 0,09 | 0,18 | |
| 4,70 | 23,50 | —0,20 | 0,04 | 0,20 | |
| 4,80 | 48,00 | —0.10 | 0,01 | 0,10 | |
| 4,90 | 39,20 | ||||
| 5,00 | 45,00 | +0,10 | 0,01 | 0,09 | |
| 5,10 | 10,20 | +0,20 | 0,04 | 0,08 | |
| 5,20 | 5,20 | +0,30 | 0,09 | 0,09 | |
| 5,30 | 15,90 | +0,40 | 0,16 | 0,48 | |
| n=40 | 196,20 | 1,22 |
Таблица 35
| xi | ni | xini | xi-
| (xi- )2
| (xi- )2ni
|
| 4,70 | 32,90 | —0,20 | 0,04 | 0,28 | |
| 4,80 | 57,60 | —0.10 | 0,01 | 0,12 | |
| 4,90 | 49,00 | ||||
| 5,00 | 40,00 | +0,10 | 0,01 | 0,08 | |
| 5,10 | 10,20 | +0.20 | 0,04 | 0,08 | |
| 5,20 | 5,20 | +0,30 | 0,09 | 0,09 | |
| n=40 | 194,90 | 0.65 |
Как обычно при сравнении характеристик вариационных рядов, средние арифметические сравниваются между собой и коэффициенты вариации (или средние квадратические отклонения) —между собой.
На основании сравнения средних арифметических 1 = 4,9 м и 2=4,9 м) приходим к выводу, что новая методика не привела к улучшению результатов и потому ее следует считать неэффективной.
Сравнение коэффициентов вариации (V1—3,5% и V2-2,6%) показывает некоторое преимущество экспериментальной группы, результаты которой оказались более однородными.
Таким образом, если методика применялась непродолжительное время и не могла еще показать существенных сдвигов, оцениваемых средними арифметическими найденные характеристики показывают на определенное улучшение в результатах, Если же методика внедрена давно, ее следует считать неэффективной.
Здесь приведены не все случаи, где метод вариационных рядов (он называется еще метод средних величин) нашел свое применение в спортивной практике. Здесь собраны наиболее простые и распространенные случаи, чаще всего встречающиеся в практике тренера.
|
|
|
Кроме дискретных вариационных рядов, существуют еще ряды интервальные.
Интервальным называется такой ряд, у которого каждый вариант выражен интервалом—границами значений от... и до...
Интервальные ряды используют, если число вариант в дискретном ряде очень велико при этом варианты распределяют по интервала, каждый из которых содержит некоторый диапазон значений изучаемого признака.
Первая задача, которую необходимо решить при распределении, состоит в том, чтобы разбить весь диапазон варьирования признака (между минимальной и максимальной вариантами) на интервалы. Эта задача требует определения числа интервалов и ширины каждого из них.
Приближенно число интервалов k можно оценить исходя из объема выборки n. Делается это одним из следующих способов:
1) по формуле Стерджеса:
;
2) с помощью таблицы
Таблица 36
Выбор числа интервалов
| Объем выборки, n | Число интервалов, k |
| 25 – 40 | 5 - 6 |
| 40 – 60 | 6 – 8 |
| 60 – 100 | 7 – 10 |
| 100 – 200 | 8 – 12 |
| Больше 200 | 10 - 15 |
Если число интервалов выбрано, то ширина каждого из них определяется по формуле:
,
где h – ширина интервалов; x max и x min максимальная и минимальная варианты; k – число интервалов.
Округление производится в сторону увеличения, чтобы не уменьшать общий диапазон варьирования признака.
Теперь остается наметить границы интервалов. Нижняя граница первого интервала выбирается так, чтобы минимальная варианта x min попала примерно в середину этого интервала. Отсюда нижняя граница первого интервала определяется как
,
где x min минимальная варианта; h – ширина интервалов.
Прибавив к этой величине ширину интервала, найдем нижнюю границу второго интервала. Это одновременно и верхняя граница предыдущего (первого) интервала. Аналогично находим границы всех оставшихся интервалов.
После того как намечены границы всех интервалов, остается распределить по этим интервалам выборочные варианты. Однако при этом возникает вопрос, как поступать в тех случаях, если какая-либо из вариант попадает точно на границу соседних интервалов. Такие варианты могут быть с одинаковым основанием отнесены к любому из соседних интервалов, и, чтобы исключить неопределенность такой ситуации, уменьшают нижние границы всех интервалов на величину, равную точности измерения исследуемого признака.
|
|
|
Рассмотрим еще раз пример 15.
1. Объем выборки (число вариант) – 40.
2. По таблице число интервалов – 5
3. Ширина интервала h = (5,3 – 4,6)/5=0,14
4. Нижняя граница первого интервала 4,6 – 0,14/2 = 4,53
5. Нижняя граница второго интервала 4,53 + 0,14 = 4,67, и т.д.
Распределяем варианты и интервальный ряд имеет такой вид (табл. 37).
Таблица372
| xi | ni |
| 4,53—4,67 | |
| 4,67—4,81 | |
| 4,81—4,95 | |
| 4,95—5,09 | |
| 5,09—5,23 | |
| n=40 |
Для вычисления показателей вариации интервальных рядов следует интервальный ряд преобразовать в дискретный. Для этого в каждом интервале находится его среднее значение — оно принимается за соответствующий вариант. Дальнейшие вычисления производятся так, как было показано выше.
