Примеры решения задач

Пример 1. Для измерения показателей преломления прозрачных веществ используют интерферометр (см. схему). Здесь S – узкая щель, освещаемая монохроматическим светом (λ₀ = 0.589 мкм); 1 и 2 – две одинаковые трубки с воздухом, длина каждой из которых l = 10 см; Д – диафрагма с двумя щелями; Л – собирающая линза. Когда воздух в трубке 2 заменили аммиаком, то ранее наблюдавшаяся на экране Э интерференционная картина сместилась вверх на N = 17 полос. Определить показатель преломления ń аммиака, если для воздуха n = 1.00029.

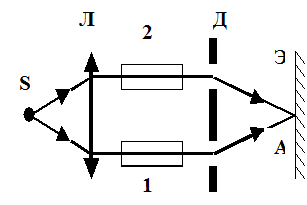Решение. Согласно принципу Гюйгенса, две щели в освещаемой диафрагме можно рассматривать как вторичные источники световых волн. Так как при этом на диафрагму падает свет от одного источника S, то обе щели являются когерентными источниками и на экране возникает интерференционная картина.

Результат интерференции света в какой-либо точке А экрана определяется из соотношения

, (1)

где Δ = L₂ – L₁ – оптическая разность хода лучей S1A, S2A; k – целое число; λ₀ – длина световой волны в вакууме.

Так, для светлых интерференционных полос имеем

(2)

где k – номер данной полосы (отсчет ведется от центральной полосы, для которой k = 0).

Оптическая длина пути, проходимого световым лучом в однородной среде с показателем преломления n,

L = ns, (3)

где s – геометрическая длина пути луча.

Замена воздуха аммиаком в трубке 2 вызвала изменение оптической длины пути L₂ светового луча S2A на величину

δ = ńl –nl. (4)

На столько же изменилась величина Δ = L₂ – L₁. При этом, согласно формуле (1), изменилось условие интерференции света в точке А.

В процессе замены воздуха аммиаком, когда величина Δ непрерывно изменялась, в точке А экрана постепенно сменяли друг друга светлые и темные интерференционные полосы – интерференционная картина перемещалась по экрану. Ее смещению на одну полосу соответствует в формуле (2) изменение числа k на единицу и, следовательно, изменение Δ на величину ±λ₀. Значит, при смещении интерференционной картины на N полос оптическая разность хода Δ изменилась на величину ±Nλ₀. Но это изменение выражается формулой (4), поэтому

ńl – nl =±Nλ₀. (5)

Знак в правой части (5) определяется направлением смещения интерференционной картины на экране. Действительно, рассмотрим центральную интерференционную полосу (k = 0). Когда в обеих трубках был воздух, она располагалась на экране на равных расстояниях от щелей в диафрагме. Перемещение полосы вверх в процессе замены воздуха в трубке 2 аммиаком свидетельствует, как это видно из чертежа, об увеличении оптической длины пути L₁ луча S1A. Но для центральной интерференционной полосы, как бы она ни перемещалась по экрану, всегда

Δ = L₂ – L₁ = ± kλ₀ = 0.

Следовательно, оптическая длина пути L₂ луча S2A также увеличилась. Очевидно, это могло произойти только вследствие неравенства ń > n. Таким образом, отбросив знак «минус» в правой части (5), получим

ń = n + (N λ₀ )/ l = 1.00039.

Пример 2. Для уменьшения потерь света при отражении от стекла на поверхность объектива (n = 1,7) нанесена тонкая прозрачная пленка (n = 1,3). При какой наименьшей толщине ее произойдет максимальное ослабление отраженного света, длина волны которого приходится на среднюю часть видимого спектра (λ = 0,56 мкм)? Считать, что лучи падают нормально к поверхности объектива.

Решение. Свет, падая на объектив, отражается как от передней, так и от задней поверхностей тонкой пленки. Ход лучей для случая их наклонного падения изображен на схеме. Отраженные лучи 1 и 2 интерферируют. Условие минимума интенсивности света при интерференции выражается формулой

где Δ – оптическая разность хода; (m = 2k + 1) – нечетное число (k = 0, 1, 2, 3,…); λ₀ – длина световой волны в вакууме, т. е.

(1)

Оптическая разность хода лучей, отраженных от двух поверхностей тонкой пленки, окруженной одинаковыми средами, определяется формулой

(2)

где h – толщина пленки; n – показатель преломления пленки; b – угол преломления. В данном случае пленка окружена различными средами – воздухом (n = 1) и стеклом (n = 1.7). Из неравенства n₁<n<n₂ следует, что оба луча 1 и 2, отражаясь от границы с оптически более плотной средой, «теряют» полуволну. Так как это не влияет на их разность хода, то в (2) следует отбросить член λ₀/2. Кроме того, полагая b = 0, получим

(3)

Из равенств (1) и (3) находим толщину пленки:

Учитывая, что h – положительная величина и что значению h_min соответствует k = 0, получим

h_min = λ₀/4n = 0.11 мкм.

Пример 3. Монохроматический свет с длиной волны λ = 7 × 10^–7 м падает нормально на дифракционную решетку с периодом d = 2 × 10^–6 м. Длина решетки l = 4 × 10^–2 м. Определить угловую ширину дифракционного максимума Δψ первого порядка.

Решение. Между двумя главными максимумами, соответствующими разности хода лучей от соседних щелей d· sin φ= kλ, где k = 0, ± 1, ± 2, …, лежат (N – 1) добавочных минимумов, определяемых разностью хода

где c может принимать целые значения от 1 до (N – 1).

Угловое расстояние между главными максимумом и соседним минимумом определяется требованием, чтобы разность хода возросла на λ/N, т. е.

или

,

отсюда

что составляет полуширину максимума.

но N = l / d; Δψ – полная ширина максимума. Угол j определим из условия первого максимума на дифракционной решетке:

d·sin φ = λ,

откуда

cos φ = 0.935.

Следовательно,

рад.

Пример 4. Экран Р находится на расстоянии 4 м от точечного монохроматического источника света. Посередине между экраном и источником света помещена диафрагма М с круглым отверстием. При каком радиусе отверстия центр дифракционных колец, наблюдаемых на экране Р, будет наиболее темным, если длина волны источника света равна 6 × 10^–7 м?

Решение. Проведем из точки А ряд концентрических сфер с радиусами, отличающимися на λ/2, и тем самым разобьем отверстие в диафрагме М на зоны Френеля (см. схему). Зная число зон, уложившихся в отверстии, можно определить освещенность в точке А экрана Р.

Пусть отверстие пропускает m зон Френеля, тогда радиус m -й зоны r_m есть одновременно радиус отверстия:

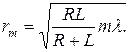
Очевидно, что освещенность центра колец, наблюдаемых на экране Р, минимальна при m = 2, так как в этом случае действие одной половины зон компенсирует действие другой половины.

Подставляя числовые данные, получаем

м.

Пример 5. Определить угол φ между главными плоскостями поляризатора и анализатора, если интенсивность света Ι, прошедшего через эту систему, уменьшилась в восемь раз. Поглощением света пренебречь.

Решение. Интенсивность света, прошедшего через систему «поляризатор – анализатор», меняется по закону Малюса:

I₂ = I₁·cos² φ = 0.5·I₀·cos² φ.

Согласно условию задачи,

отсюда

,

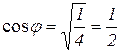φ = 60°.

Из закона Малюса (I₂ = I₁· cos² φ) следует, что при повороте осей поляризатора и анализатора на угол φ = 90 ° свет через такую систему проходить не будет (I₂ = 0).

Пример 6. Естественный свет падает под углом Брюстера на поверхность стекла (n = 1.6). Определить коэффициент отражения.

Решение. Коэффициент отражения ρ показывает, какую долю от интенсивности падающего света I составляет интенсивность отраженного света I', т. е.

ρ = I'/I. (1)

Свет, отраженный от диэлектрика под углом Брюстера, полностью поляризован. При этом в отраженном луче присутствуют лишь световые колебания, перпендикулярные плоскости падения. Поэтому на основании формулы Френеля

(2)

где I_┴ и I'_┴ – интенсивности падающего и отраженного света, у которого колебания светового вектора перпендикулярны плоскости падения; a – угол падения; b – угол преломления, и соотношения (a_Б + b = π/2) получим

(3)

Так как в естественном свете величина составляет половину от полной интенсивности I, то из (1), (3) следует

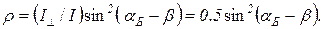(4)

Углы a_Б и b можно найти, зная показатель преломления стекла n. По закону Брюстера, tg a_Б = n =1.6. Отсюда a_Б = 58 °, b = 90 ° – 58 ° = 32 °; a_Б – b = 26 °.

Теперь из (4) получим

ρ = 0.5 sin² 26° = 0.10 или 10 %.

Пример 7. Красная граница фотоэффекта для цезия равна
λ₀ = 6.53 × 10^–7 м. Определить скорость фотоэлектронов V при облучении цезия фиолетовыми лучами с длиной волны λ = 5 × 10^–7 м (h = 6.625 × 10^–34 Дж × с,
с = 3 × 10⁸ м/с, т = 9.11 × 10^–31 кг).

Решение. Скорость фотоэлектронов может быть определена из уравнения Эйнштейна для фотоэффекта

.

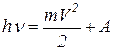Работу выхода электрона из цезия можно определить, зная красную границу фотоэффекта, т. е. ту минимальную энергию, при которой еще наблюдается фотоэффект:

.

Определяя из уравнения Эйнштейна скорость электрона, получим

В системе СИ скорость

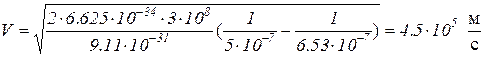
Пример 8. Исследования спектра излучения Солнца показывают, что максимум спектральной плотности энергетической светимости соответствует длине волны 0.5 мкм.

Принимая Солнце за абсолютно черное тело, определить:

а) энергетическую светимость Солнца;

б) поток энергии, излучаемой Солнцем;

в) энергетическую освещенность поверхности Земли при нормальном падении лучей без учета поглощения в атмосфере.

Решение. а)Энергетическая светимость R_Э абсолютно черного тела выражается формулой Стефана – Больцмана

R_Э = σТ⁴, (1)

где σ – постоянная Стефана – Больцмана; Т – абсолютная температура излучающей поверхности.

Температура может быть определена из закона смещения Вина

, (2)

где λ₀ – длина волны, на которую приходится максимум спектральной плотности энергетической светимости абсолютно черного тела; b – постоянная Вина.

Выразив из закона смещения Вина температуру Т и подставив ее в (1), получим

(3)

Выразим величины в системе СИ:

σ = 5.67 × 10^–8 Вт/(м² × К⁴);

b = 2.9 × 10^–3 м × К;

λ₀ = 0.5 мкм = 5 × 10^–7 м.

Подставив эти числовые значения в (3) и произведя вычисления, получим

R_Э Вт/м².

б)Поток энергии Р, излучаемой Солнцем, равен произведению энергетической светимости Солнца на площадь S его поверхности:

P = R_Э S,

или

P = 4π r² R_Э, (4)

где r = 6.96 × 10⁸ м – радиус Солнца.

Подставив эти значения в (4), найдем

Р = Вт.

в)Энергетическую освещенность Е_Э поверхности Земли определим, если разделим поток энергии Р, излучаемой Солнцем, на площадь S' поверхности сферы, радиус которой равен среднему расстоянию от Земли до Солнца:

Е_Э = Р/ S',

или

Е_Э = (5)

где R = 1.50 × 10¹¹ м – среднее расстояние от Земли до Солнца.

Подставив числовые значения в (5), получим

Е_Э = Вт/м².