2.4.1. Определение. Пусть дана неоднородная система линейных уравнений
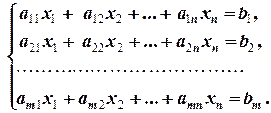 (2.4.1)
(2.4.1)
Рассмотрим однородную систему
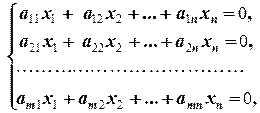 (2.4.2)
(2.4.2)
у которой матрица коэффициентов совпадает с матрицей коэффициентов системы (2.4.1). Тогда система (2.4.2) называется приведённой однородной системы (2.4.1).
2.4.2. Теорема. Общее решение неоднородной системы равно сумме некоторого частного решения неоднородной системы и общего решения приведённой однородной.
Таким образом, для нахождения общего решения неоднородной системы (2.4.1) достаточно:
1) Исследовать её на совместность. В случае совместности:
2) Найти общее решение приведённой однородной этой системы.
3) Найти какое-либо частное решение исходной (неоднородной).
4) Сложив найденные частное решение и общее решения приведённой, найти общее решение исходной системы.
2.4.3. Упражнение. Исследовать систему на совместность и в случае совместности найти её общее решение в виде суммы частного и общего приведённого.
а) 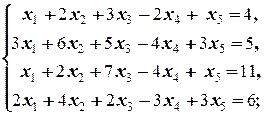 б)
б) 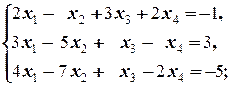
в) 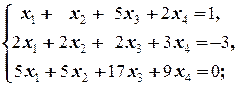 г)
г) 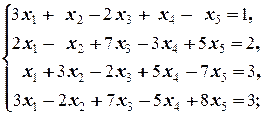
д) 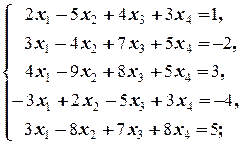 е)
е) 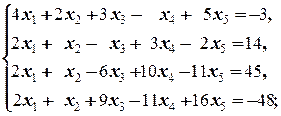
ж) 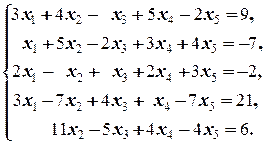
Решение. а) Для решения задачи применяем вышеуказанную схему:
1) Исследуем систему на совместность (методом окаймления миноров): Ранг основной матрицы равен 3 (см. решение упр. 2.2.5, а), причём ненулевой минор максимального порядка 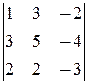 составлен из элементов 1-й, 2-й, 4-й строк и 1-го, 3-го, 4-го столбцов. Для нахождения ранга расширенной матрицы окаймляем его 3-ей строкой и 6-м столбцом расширенной матрицы:
составлен из элементов 1-й, 2-й, 4-й строк и 1-го, 3-го, 4-го столбцов. Для нахождения ранга расширенной матрицы окаймляем его 3-ей строкой и 6-м столбцом расширенной матрицы: 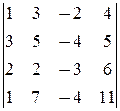 =0. Значит, rg A = rg
=0. Значит, rg A = rg 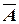 =3, и система совместна. В частности, она равносильна системе
=3, и система совместна. В частности, она равносильна системе
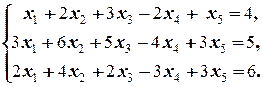 (2.4.3)
(2.4.3)
2) Найдём общее решение X 0 приведённой однородной этой системы
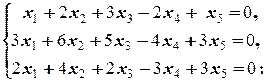 .
.
X 0={(-2 a - 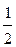 b; a;
b; a; 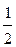 b; b; b) | a, b Î R }
b; b; b) | a, b Î R }
(см. решение упр. 2.2.5, а)).
3) Найдём какое-либо частное решение xч исходной системы. Для этого в системе (2.4.3), равносильной исходной, свободные неизвестные x 2 и x 5 полагаем равными, например, нулю (это наиболее удобные данные):
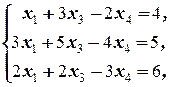
и решаем полученную систему: x 1=- 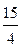 , x 3=-
, x 3=- 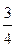 , x 4=-5. Таким образом, (-
, x 4=-5. Таким образом, (- 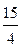 ; 0; -
; 0; - 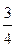 ; -5; 0) ¾ частное решение системы.
; -5; 0) ¾ частное решение системы.
4) Находим общее решение Xн исходной системы:
Xн ={ xч }+ X 0 ={(- 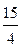 ; 0; -
; 0; - 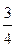 ; -5; 0)} + {(-2 a -
; -5; 0)} + {(-2 a - 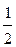 b; a;
b; a; 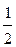 b; b; b)}=
b; b; b)}=
={(- 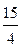 -2 a -
-2 a - 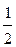 b; a; -
b; a; - 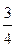 +
+ 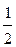 b; -5+ b; b)}.
b; -5+ b; b)}.
Замечание. Сравните полученный ответ со вторым ответом в примере 1.2.1 в). Для получения ответа в первом виде для 1.2.1 в) в качестве базисных неизвестных берутся x 1, x 3, x 5 (минор при которых тоже не равен нулю), а в качестве свободных ¾ x 2 и x 4.
§3. Некоторые приложения.
3.1. К вопросу о матричных уравнениях. Напоминаем, что матричным уравнением над полем F называется уравнение, в котором в качестве неизвестной выступает некоторая матрица над полем F.
Простейшими матричными уравнениями являются уравнения вида
AX = B, XA = B (2.5.1)
где A, B ¾ данные (известные) матрицы над полем F, а X ¾ такие матрицы, при подстановке которых уравнения (2.5.1) обращаются в верные матричные равенства. В частности, матричный метод определённых систем сводится к решению матричного уравнения.
В случае, когда матрицы A в уравнениях (2.5.1) невырожденны, они имеют решения соответственно X = A 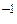 B и X = BA
B и X = BA 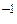 .
.
В случае, когда хотя бы одна из матриц в левой части уравнений (2.5.1) является вырожденной, данный метод уже не годится, так как соответствующая обратная матрица A 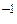 не существует. В этом случае нахождение решений уравнений (2.5.1) сводится к решению систем.
не существует. В этом случае нахождение решений уравнений (2.5.1) сводится к решению систем.
Но прежде введём некоторые понятия.
Множество всех решений системы назовём общим решением. Отдельно взятое решение неопределённой системы назовём её частным решением.
3.1.1. Пример. Решитьматричное уравнение над полем R.
а) X 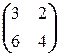 =
= 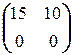 ; б)
; б) 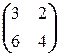 X =
X = 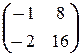 ; в)
; в) 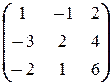 X =
X =  .
.
Решение. а) Так как 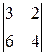 =0, то формула X = A
=0, то формула X = A 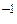 B для решения этого уравнения не годится. Если в произведении XA = B матрица A имеет 2 строки, то матрица X имеет 2 столбца. Число строк X должно совпасть с числом строк B. Поэтому X имеет 2 строки. Таким образом, X ¾ некоторая квадратная матрица второго порядка: X =
B для решения этого уравнения не годится. Если в произведении XA = B матрица A имеет 2 строки, то матрица X имеет 2 столбца. Число строк X должно совпасть с числом строк B. Поэтому X имеет 2 строки. Таким образом, X ¾ некоторая квадратная матрица второго порядка: X = 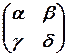 . Подставим X в исходное уравнение:
. Подставим X в исходное уравнение:
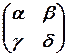
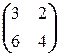 =
= 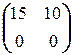 . (2.5.2)
. (2.5.2)
Перемножая матрицы в левой части (2.5.2), приходим к равенству
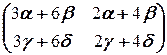 =
= 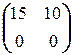 . (2.5.3)
. (2.5.3)
Две матрицы равны тогда и только тогда, когда они одинаковых размерностей и равны их соответствующие элементы. Поэтому (2.5.3) равносильно системе
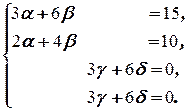
Эта система равносильна системе
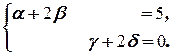
Решая её, например, методом Гаусса, приходим к множеству решений (5-2 b, b, -2 d, d), где b, d независимо друг от друга пробегают R. Таким образом, X = 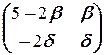 .
.
б) Аналогично а) имеем X = 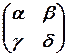 и.
и.
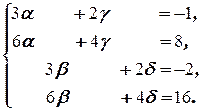
Эта система несовместна (убедитесь в этом!). Поэтому данное матричное уравнение решений не имеет.
в) Обозначим это уравнение через AX = B. Так как A имеет 3 столбца, а B имеет 2 столбца, то X ¾ некоторая матрица размерности 3´2: X = 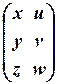 . Поэтому имеем следующую цепочку равносильностей:
. Поэтому имеем следующую цепочку равносильностей:
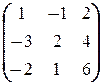
 =
=  Û
Û 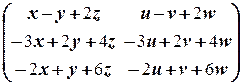 =
=  Û
Û
Û 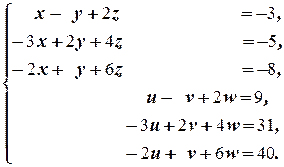
Решаем последнюю систему методом Гаусса (комментарии опускаем)
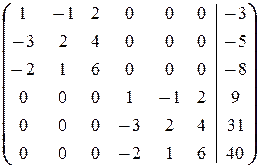 ®
® 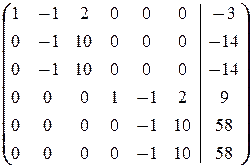 ®
®
® 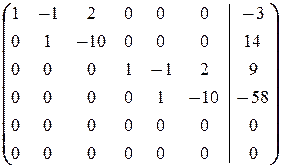 .
.
Таким образом, приходим к системе
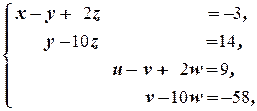
решением которой является (11+8 z, 14+10 z, z, -49+8 w, -58+10 w, w) где z, w пробегают независимо друг от друга R.
Ответ: а) X = 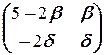 , b, d Î R.
, b, d Î R.
б) Решений нет.
в) X = 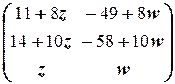 z, w Î R.
z, w Î R.
3.2. К вопросу о перестановочности матриц. В общем случае произведение матриц неперестановочно, то есть если A и B такие, что AB и BA определены, то, вообще говоря, AB ¹ BA. Но пример единичной матрицы E показывает, что возможна и перестановочность AE = EA для любой матрицы A, лишь бы AE и EA были определены.
В этом пункте мы рассмотрим задачи на нахождение множества всех матриц, перестановочных с данной.
3.2.1. Пример. Найти все матрицы, перестановочные с матрицей A (над полем R):
а) 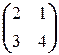 ; б)
; б) 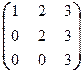 .
.
Решение. а) Допустим, X ¾ перестановочна с A: AX = XA. Легко видеть, что X ¾ квадратная матрица второго порядка: X = 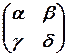 . Поэтому имеем следующую цепочку равносильностей:
. Поэтому имеем следующую цепочку равносильностей:
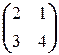
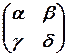 =
= 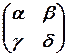
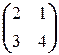 Û
Û 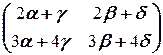 =
= 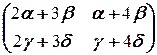 Û
Û
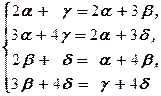 Û
Û 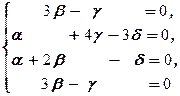 Û
Û 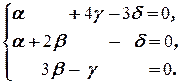
Решая полученную однородную систему, получаем 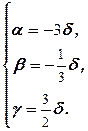 Таким образом, X =
Таким образом, X = 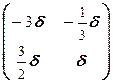 ¾ матрицы, перестановочные с
¾ матрицы, перестановочные с 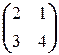 , d ¾ любое число.
, d ¾ любое число.
б) Аналогично предыдущему, матрица X, перестановочная с A = 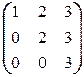 , имеет вид
, имеет вид 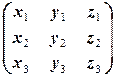 . Поэтому имеем следующую цепочку равносильностей:
. Поэтому имеем следующую цепочку равносильностей:
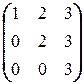
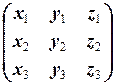 =
= 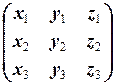
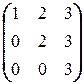 Û
Û
Û 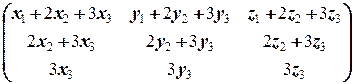 =
= 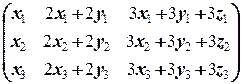
Û 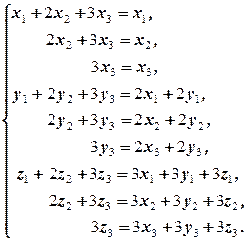
В последней системе из 3-го, 1-го и 6-го уравнений последовательно получаем x 3= x 2 = y 3 =0. Учитывая это, из системы получаем систему
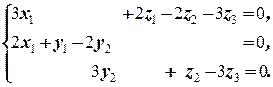
Неизвестные x 1, y 2 и z 3 могут принимать любые значения: x 1= a, y 2= b, z 3= g. Тогда 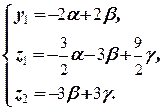
Таким образом, X = 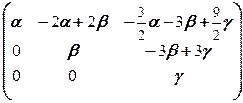 .
.
Ответ. а) X ¾ множество матриц вида 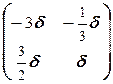 , где d ¾ любое число.
, где d ¾ любое число.
б) X ¾ множество матриц вида 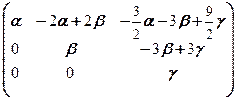 , где a, b и g ¾ любые числа.
, где a, b и g ¾ любые числа.
 2015-03-08
2015-03-08 15110
15110
