Производные и дифференциалы

Некоторых математических функций

Производная. Определение. Если f (x) – непрерывная функция одной переменной, то ее производной называется

.

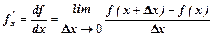Дифференциал. Определение. ,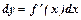

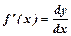
Дифференцирование арифметических комбинаций.

(u, v, w – дифференцируемые функции, a и b - постоянные)

( a u + b v)’ = a u’ + b v’, d( a u + b v)’ = a du + b dv’,

(u v)’ =u’v +u v’, (u v)’ =udv + vdu,

(u v w)’ = u’ v w + u v’ w + u v w’,

d(u v w) = v w du + u w d v + u v dw,

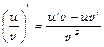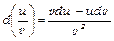, (v¹ 0).

Производные элементарных функций.

Функция	Производная
C
x
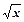
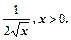
1/x	-1/x2
xn	nxn-1
ex	ex
ax	axlna
lnx	1/x
Sin x	Cos x
Cos x	- sin x
tg x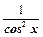
ctg x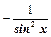

Интеграл