2015-10-22
1245
Розв’яжемо рівняння, складені за методом контурних струмів відносно струму k -вітки, що входить тільки в k - контур (хорда, вітка зв’язку).
де 
- головний визначник системи, 
- відповідне алгебраїчне допов-нення.
- має розмірність провідності (Сім),а кожна складова 
являє собою струм, створений у k -вітці контурною ЕРС 
.Наприклад, 
- складова струму в k - вітці створена, контурною ЕРС 
.
Кожну контурну ЕРС можна виразити через ЕРС віток 
, згрупувати коефіцієнти при цих ЕРС і одержати вираз такого вигляду:
(4)
Це рівняння виражає принцип накладання дії джерел енергії:
струм уk- вітці дорівнює алгебраїчній сумі струмів, створених у цій вітці ок-ремо кожним джерелом кола.
Принцип дійсний для всіх лінійних електричних кіл. Якщо в схемі діє n джерел, то струм у кожній вітці буде мати n складових (часткових струмів).
Алгоритм розрахунку кола методом накладання дії джерел енергії.
1. Складне коло розкладаємо за кількістю джерел на n простих кіл, в яких діє тільки одне джерело.
2. У кожному з простих кіл розраховуємо часткові струми, викликані дією єди-ного джерела, в усіх вітках.
3. Результуючий струм у кожній вітці дорівнює алгебраїчній сумі часткових струмів, створених у цій вітці кожним джерелом окремо.
На Рис.38, а зображена схема електричного кола, яке має три вітки і дві ЕРС 
з внутрішніми опорами 
. Складаєм рівняння за методом контурних струмів:
Застосовуючи визначники, розв’язуємо систему рівнянь і знаходимо кон-турні струми:
Звідки знаходимо контурні струми:
Тут 
вхідна провідність вітки 1, чисельно дорівнює частковому струму у вітці 1, який виникає від дії ЕРС 
за умови
коли інші джерела відсутні.
те ж саме для вітки 2.
взаємна (передавальна) провідність віток 1 і 2, чисельно дорівнює частковому струму у вітці 1, який виникає від дії ЕРС 
і від-сутності джерел в інших вітках.
взаємна (передавальна) провідність віток 2 і 1.
У загальному випадку, коли коло має n віток, вхідна провідність вітки m (подвійний індекс m): 
Взаємна (передавальна) провідність між вітками k i m (різні індекси):
.
При однаковій взаємній орієнтації струму і ЕРС у вітках k i m, легко показа-ти, що:
.
Якщо у вітках k i m струм і ЕРС взаємноорієнтовані не однаково, то:
.
Саме вхідні та передавальні провідності віток є коефіцієнтами рівняння (4), що виражає принцип накладання дії джерел енергії для будь-якого складного кола з декількома ЕРС.
Використовуючи метод накладання, можна сформулювати принцип взаєм- ності:
для будь-якого лінійного кола струм 
вітці k, створений ЕРС 
, що знаходиться у вітці m, дорівнює струму 
у вітці m, створеному ЕРС 
, що знаходиться у вітці k.
У електричному колі (Рис.39, а) з одним джерелом виділено дві вітки m і k,а вся інша частина кола з пасивними елементами (опорами), виділена прямо-кутником (П). Якщо ЕРС діє у вітці m: 
, то струм 
у k -вітці:
Якщо ЕРС увімкнути у k -вітку (Рис. 37,б) то струм 
у вітці m
.
Оскільки 
то 
якщо у вітках k і m ЕРС і струм орієн-товані взаємно однаково.
Кола, які задовольняють принципу взаємності називаються оборотними.
Використовуючи принцип взаємності, можна спрощувати розрахунки деяких кіл. Наприклад, у колі Рис. 40, а визначення струму 
значно простіше при перенесенні ЕРС 
у вітку 3 (Рис. 40, б).
Приклад 3. Розрахувати струми у колі на Рис. П3 методом накладання і визначити, при якому значенні ЕРС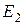 
струм 
у третій вітці дорівнюватиме 3(А). Ця задача раніше розв’язана методами контурних струмів та вузлових по-тенціалів і дійсні струми у вітках відомі, то ж скористуємся ними для перевірки розрахунку методом накладання.
Задаємо напрями струмів у вітках.
За кількістю джерел (дві ЕРС і одне джерело струму) коло розкладається на три прості (часткові) кола, в яких діє тільки одне джерело. У часткових колах видалені джерела заміняються внутрішніми опорами. Внутрішній опір іде-ального джерела ЕРС дорівнює нулю - закоротка, ідеального джерела струму –нескінченності - розрив. Будь-яким методом розраховуємо струми у вітках часткової схеми.
І) Розрахунок часткового кола з джерелом Е2. (
,Рис. П3.1, а).
Розрахунок проводимо за допомогою поступового згортання кола до еле-ментарного, і поетапного знаходження струмів в усіх вітках при поверненні до початкового кола.
1. Перетворюємо трикутник із опорів 
в зірку (показано пунк-тиром на Рис. П3.1, а) з опорами 
(Рис. П3.1, б).
.
2. Коло при цьому значно спростилось, дві вітки з послідовно з’єднаними опорами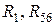 
, і 
між собою з’єднані паралельно. Еквівалентний опір паралельного з’єднання (Рис. П3.1, б):
Еквівалентний опір нерозгалуженого кола Рис. П3.1, в):
3. Струми у частковому колі позначаємодвома індексами; перший індекс – номер вітки, другий – номер джерела. Струм джерела нерозгалуженого кола, він же і струм другої вітки 
початкового кола на Рис. П3.1, а:
.
Струми у паралельних вітках(Рис. П3.1, б).
;
.
4. Визначаємо напруги 
, 
між точками а, б і б, в «зірки», які є вуз-лами «трикутника» (Рис. П3.1, б):
,
.
5. Струми у «трикутнику»:
.
Отже:
Вірність розрахунків перевіряється за балансом потужностей:
20.0.698 =0.2562.26+0.6982.10+0.3822.18+0.442.14+0.3152.20+0.0612.8;
13.96 (Вт) @ 13.94 (Вт).
ІІ) Розрахунок часткового кола з джерелом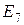 
. (
Рис. П3.2).
Розрахунок часткового кола проводимо методом контурних струмів, нап-рями яких показані на рисунку.
Розв’язок цієї системи рівнянь дає контурні струми:
Струми у вітках кола:
Самостійно перевірте вірність розрахунків за балансом потужностей.
ІІІ) Розрахунок часткового кола з джерелом J. (Е 2 = 0, Е 7 = 0, Рис. П3.3).
Розрахунок часткового кола проводиться методом вузлових потенціалів.
Приймаємо потенціал «заземленого» вузла за нульовий. Складаємо систему рівнянь для потенціалів трьох незалежних вузлів 1, 2, 3:
Результат розв’язання системи рівнянь:
Струми у вітках:
Перевірте вірність розрахунків за балансом потужностей.
IV) Накладання часткових струмів.
Значення струмів практично такі ж, як і розраховані методами контурних струмів і вузлових потенціалів.
Використовуючи вхідні та взаємні провідності, можна знайти залежність між струмом будь-якої вітки і будь-якою ЕРС схеми. Залежність струму тре-тьої вітки I 3 від ЕРС E 2: 
.
Де: 
Тепер ЕРС E2, потрібна для створення струму I 3 = 3 (А):
,
Підставляючи знайдене значення ЕРС E 2в рівняння кола, складені за будь-яким розрахунковим методом і знаходячи струм I 3, пересвідчуємся у правильності розрахунку.
