Рівняння прямої з кутовим коефіцієнтом

Розглянемо рівняння (1) із 3.2

Позначивши , отримаємо

рівняння пучка прямих, або рівняння прямої, що проходить через точку 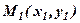у заданому напрямку. Геометричний зміст коефіцієнта зрозумілий з рис. 6.

В , де – найменший кут, на який потрібно повернути додатний напрямок осі 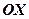навколо спільної точки 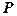до суміщення її з прямою 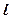. Очевидно, що якщо кут – гострий, то ; якщо ж – тупий кут, то .

Розкриємо дужки в (5) і спростимо його

де . Співвідношення (6) – рівняння прямої з кутовим коефіцієнтом. При – відрізок, який відтинає пряма на осі 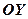(див. рис.6).

Звернемо увагу, що для переходу від загального рівняння прямої 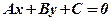до рівняння з кутовим коефіцієнтом необхідно перше розв’язати відносно

Рис.6

де позначено . Якщо ж 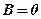, то із дослідження загального рівняння вже відомо, що така пряма перпендикулярна осі .

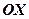Приклад

1. Перейти до рівняння з кутовим коефіцієнтом

а) ;

б) .

1. Скласти рівняння пучка прямих, які проходять через початок координат під кутами до осі Х: а) 30°; б) 45°; в) 120°; г)135°.
2. Скласти рівняння прямих, які проходять через точку М(3,-1) під кутами до осі ОХ: а) 45°; б) 60°; в) 135°; г) 150°.
3. Із точки N(5,2) під кутом 45° до осі ОХ падає промінь світла, який відбивається від осі ОХ. Знайти рівняння падаючого і відбитого променів.

Відповіді: 1. а) ; б) .

2. а) ; б) ; в) ; г) .

3. : а) ; б) ; в) ;

г) . 4. ; .