Побудуємо пряму за загальним рівнянням 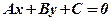 за умови, що
за умови, що 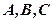 – відмінні від нуля. Для цього досить знайти дві точки, що належать цій прямій. Такі точки іноді зручніше знаходити на координатних осях.
– відмінні від нуля. Для цього досить знайти дві точки, що належать цій прямій. Такі точки іноді зручніше знаходити на координатних осях.
Покладемо 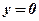 , тоді
, тоді 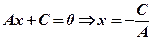 .
.
При 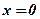
 . Позначимо
. Позначимо 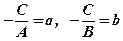 . Знайдені точки
. Знайдені точки 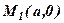 і
і  відкладемо на осях OX i OY і через них проводимо пряму
відкладемо на осях OX i OY і через них проводимо пряму
(див. рис. 2).
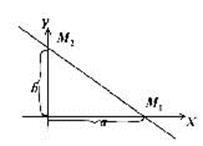
Рис.2
Від загального можна перейти до рівняння, в яке будуть входити числа 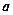 і
і 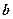 :
:
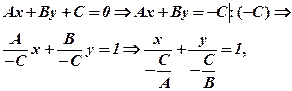
або, згідно з позначенням, отримуємо рівняння,
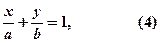
яке називається рівнянням прямої у відрізках. Числа 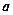 і
і 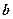 з точністю до знаку дорівнюють відрізкам, які відтинаються прямою на координатних осях.
з точністю до знаку дорівнюють відрізкам, які відтинаються прямою на координатних осях.
Приклади.
1. Записавши рівняння у відрізках, побудувати прямі
а) 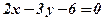 ;
;
б)  ;
;
в) 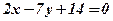 .
.
2. Знайти площу трикутника, обмеженого прямою 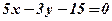 та координатними осями.
та координатними осями.
- Діагоналі ромба лежать на координатних осях, а рівняння однієї із сторін
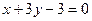 . Записати рівняння інших сторін.
. Записати рівняння інших сторін. - Скласти рівняння прямої, яка проходить через точку М(4,2) і відтинає від координатних осей трикутник, площа якого дорівнює 16 од. кв.
Відповіді: 1. а) 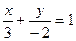 ; б)
; б) 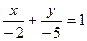 ; в)
; в) 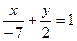 . 2. 7,5. 3.
. 2. 7,5. 3. 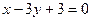 ;
; 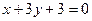 ;
; 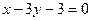 . 4.
. 4. 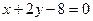 .
.
 2015-10-22
2015-10-22 2620
2620
