Перетворимо рівняння (1)
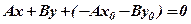 .
.
Позначивши 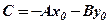 , отримаємо
, отримаємо
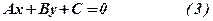
— загальне рівняння прямої.
Таким чином, прямій лінії 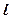 відповідає лінійне рівняння вигляду (3). Навпаки, за даним рівнянням вигляду (3), де хоча б один з коефіцієнтів
відповідає лінійне рівняння вигляду (3). Навпаки, за даним рівнянням вигляду (3), де хоча б один з коефіцієнтів 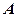 і
і 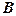 відмінний від нуля, можна побудувати пряму.
відмінний від нуля, можна побудувати пряму.
Дійсно, нехай пара чисел 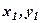 задовольняє рівняння (3), тобто
задовольняє рівняння (3), тобто
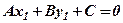 .
.
Віднімаючи останнє від (3), одержимо співвідношення 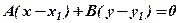 , яке визначає пряму за вектором
, яке визначає пряму за вектором 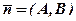 і точкою
і точкою 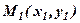 .
.
Приклади
1.Скласти загальне рівняння прямої, що проходить через точку 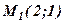 перпендикулярно вектору
перпендикулярно вектору 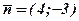 .
.
Відповідь: 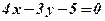 .
.
2.Задані точки 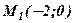 і
і 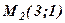 . Скласти загальне рівняння прямої, що проходить через точку
. Скласти загальне рівняння прямої, що проходить через точку 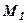 перпендикулярно вектору
перпендикулярно вектору 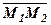 .
.
Відповідь: 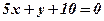 .
.
 2015-10-22
2015-10-22 772
772








