По заданной таблице yi=y(xi) значений функции найти y как функцию от x на основе:
а) интерполяционного полинома Лагранжа и Ньютона;
б) интерполяционного кубического сплайна;
в) метода минимальных квадратов для линейной, квадратичной и кубической регрессии.
| X | ||||||||
| Y | -1 |
г) интерполяционного тригонометрического полинома
| X | ||||||||
| Y | -4 | -2 |
Интерполяционный полином Лагранжа.
Задаем таблицу значений функции
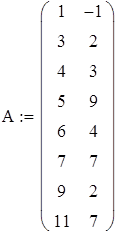
Вводим функцию интерполяционного полинома Лагранжа
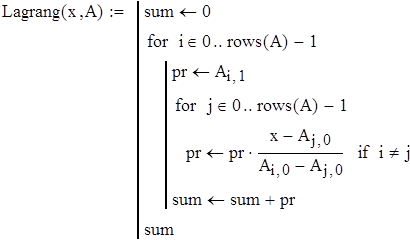
Выводим минимальное и максимальное значение аргумента
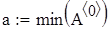
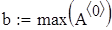
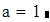
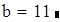
Вводим количество точек и шаг
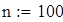
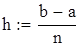
Устанавливаем счетчики
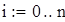
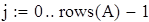
Табулируем функцию
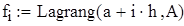
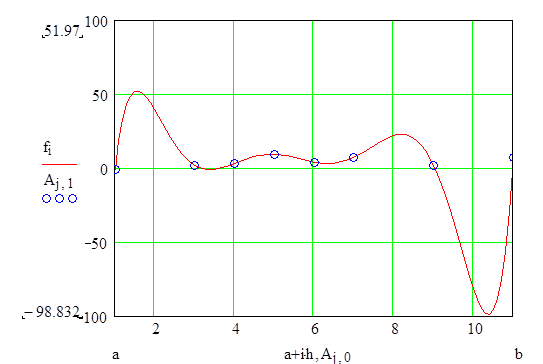
Строим график функции интерполяционного полинома Лагранжа
 2015-10-22
2015-10-22 514
514








