Интерполяционный тригонометрический полином

Задаем таблицу значений функции

Считаем число значений таблицы и задаем мнимую единицу

Устанавливаем счетчики

Считаем значение спектра

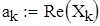
Вводим функцию интерполяционного тригонометрического полинома в случае четного числа узлов

Устанавливаем счетчики

Строим функцию интерполяционного тригонометрического полинома

Варианты заданий к лабораторной работе №6

По заданной таблице y_i=y(x_i) значений функции найти y как функцию от x на основе:

а) интерполяционного полинома Лагранжа и Ньютона;

б) интерполяционного кубического сплайна;

в) метода минимальных квадратов для линейной, квадратичной и кубической регрессии.

Вариант	Значения функции
-3					-5
				-2		-6
				-1	-4
						-1
				-1
		-1

г) интерполяционного тригонометрического полинома

Вариант	y(0)	y(1)	y(2)	y(3)	y(4)	y(5)	y(6)	y(7)
					-4			-
					-4		-3
								-
						-4	-5	-
		-4				-4
			-5	-2				-
								-5
								-

Содержание отчета

Отчет должен содержать:

1. титульный лист;

2. постановку задачи (согласно варианту);

3. краткое описание методов решения задачи Коши;

4. программную реализацию данных методов;

5. выводы о проделанной работе.

Введение 3

1 Численное интегрирование 4

1.1 Основные методы численного интегрирования 4

1.2 Пример выполнения лабораторной работы №1 10

1.3 Варианты заданий к лабораторной работе №1 12

2 Методы решения нелинейных уравнений 13

2.1 Метод половинного деления 13

2.2 Метод хорд (метод линейной интерполяции) 14

2.3 Метод секущих 16

2.4 Метод Ньютона 18

2.5 Пример выполнения лабораторной работы №2 19

2.6 Варианты заданий к лабораторной работе №2 23

3 Прямые методы решения систем линейных алгебраических уравнений 24

3.1 Метод Гаусса для решения систем линейных алгебраических уравнений. 24

3.2. Алгоритм LU-разложения. 27

3.3. Метод прогонки. 30

3.4 Пример выполнения лабораторной работы №3 34

3.5 Варианты заданий к лабораторной работе №3 40

4 Итерационные методы решения систем линейных алгебраических уравнений 42

4.1. Итерационные методы Якоби и Зейделя. 42

4.2. Каноническая форма итерационных методов. 44

4.3. Вариационно-итерационные методы решения СЛАУ. 46

4.4 Пример выполнения лабораторной работы №4 48

4.5 Варианты заданий к лабораторной работе №4 53

5 Методы решения задачи Коши 54

5.1. Метод Эйлера. 54

5.2. Метод Рунге-Кутта. 55

5.3 Пример выполнения лабораторной работы №5 57

5.4 Варианты заданий к лабораторной работе №5 60

6 Методы приближения функций 62

6.1. Интерполяционный полином Лагранжа и Ньютона. 63

6.2 Интерполяционный кубический сплайн. 68

6.3 Понятие о методе наименьших квадратов. 69

6.4 Интерполяционный тригонометрический полином 72

6.5 Пример выполнения лабораторной работы №6 75

6.6 Варианты заданий к лабораторной работе №6 85

Чистяков Александр Евгеньевич

Савицкий Олег Анатольевич

Чистякова Татьяна Алексеевна

Руководство к лабораторным работам

по курсу «Численные методы»

Ответственный за выпуск

Компьютерная верстка

Редактор