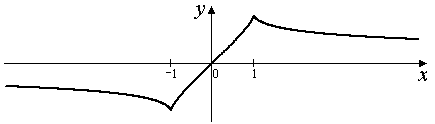Перед решением примера на исследование функции и построение графика необходимо проработать теоретический материал (см. Н.С. Пискунов, том I, гл. У, §§ I-II).
Дайте ответы на контрольные вопросы.
1. Какая функция называется возрастающей (убывающей) на данном промежутке?
2. Что такое экстремум функции?
3. Каково необходимое условие экстремума? Является ли оно достаточным?
4. Каковы достаточные признаки экстремума?
5. Что значит график функции выпуклый(вогнутый) на данном промежутке?
6. Что такое асимптота графика? Какие бывают асимптоты?
Общее исследование функций и построение графиков удобно выполнять по следующей схеме.
Общая схема исследования и построения графика
1. Найти область определения функции.
2. Найти точки разрыва функции и выяснить их характер.
3. Выяснить, является ли функция четной, нечетной, периодической.
4. Найти точки пересечения графика функции с осями координат и интервалы знакопостоянства функции.
5. Найти точки экстремума, интервалы возрастания и убывания функции.
6. Найти точки перегиба графика и интервалы выпуклости и вогнутости.
7. Найти асимптоты графика.
8. Построить график функции, используя все полученные результаты. Если их окажется недостаточно, то следует найти ещё несколько точек графика, исходя из уравнения функции.
Построение графика функции целесообразно выполнять по его элементам вслед за выполнением отдельных пунктов исследования.
Пример Исследовать функции и построить их графики
1) 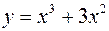 2)
2) 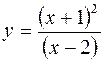
3) 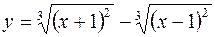 4)
4) 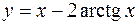
Решение 1) 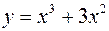
1. Область определения функции 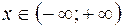
2. Точек разрыва нет, функция всюду непрерывна.
3. Функция не является ни четной, ни нечетной, ни периодической.
4. При 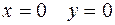 . А при
. А при 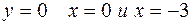 . Это означает, что график функции пересекает координатные оси в точках
. Это означает, что график функции пересекает координатные оси в точках 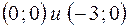 . Полученные точки сразу нанесите на координатную плоскость. Интервалы, где функция сохраняет знак, определяются условиями, что их границами могут быть только точки пересечения с осью OX, точки разрыва и границы области определения. Для данной функции такими точками могут быть точки
. Полученные точки сразу нанесите на координатную плоскость. Интервалы, где функция сохраняет знак, определяются условиями, что их границами могут быть только точки пересечения с осью OX, точки разрыва и границы области определения. Для данной функции такими точками могут быть точки 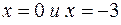 . Определяем знак функции в интервалах
. Определяем знак функции в интервалах 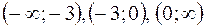 , получаем:
, получаем:
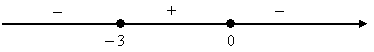
5. Находим производную 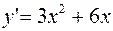 .
.
Критические точки 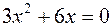 , следовательно,
, следовательно, 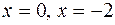 . Других критических точек нет, поскольку производная всюду существует. Используем достаточное условие монотонности функции и первый достаточный признак экстремума, составим таблицу.
. Других критических точек нет, поскольку производная всюду существует. Используем достаточное условие монотонности функции и первый достаточный признак экстремума, составим таблицу.
Таблица
| x | 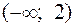 | -2 | 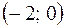 | 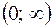 | |
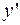 | + | - | + | ||
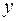 | возр. | max | убыв. | min | возр. |
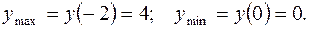
Нанесите на координатную плоскость точки экстремума и покажите пунктиром предполагаемое поведение функции.
6. Для нахождения интервалов выпуклости и вогнутости находим вторую производную 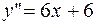 .
.
Критическая точка второго рода 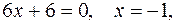 других критических точек нет, так как вторая производная всюду существует. Используем условие экстремума. (См. табл.)
других критических точек нет, так как вторая производная всюду существует. Используем условие экстремума. (См. табл.)
Таблица
 | 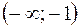 | -1 | 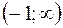 |
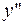 | - | - | |
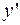 | выпукла | перегиб | вогнута |
График функции имеет точку перегиба 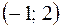 , ее ординату находим из выражения функции. Нанесите эту точку на координатную плоскость.
, ее ординату находим из выражения функции. Нанесите эту точку на координатную плоскость.
7. Вертикальных асимптот нет, так как функция всюду непрерывна. Определяем наклонную асимптоту, ее уравнение 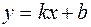 . Коэффициенты
. Коэффициенты 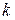 и
и 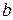 находим по формулам
находим по формулам
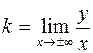
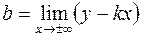
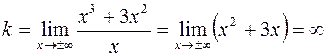 .
.
Угловой коэффициент асимптоты не существует, поэтому наклонной асимптоты нет.
Уточним график в правой полуплоскости, так как характерных точек там нет, для этого найдем 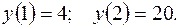
Окончательно строим график.
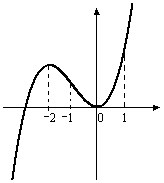 |
Решение 2) 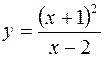
1. Область определения 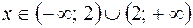 .
.
2. Точка разрыва 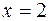 , исследуем характер разрыва, для этого, найдем односторонние пределы в этой точке:
, исследуем характер разрыва, для этого, найдем односторонние пределы в этой точке:
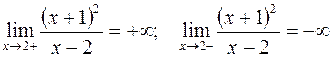
отсюда следует, что 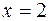 - точка разрыва второго рода. Попутно можно заметить, что есть вертикальная асимптота с уравнением
- точка разрыва второго рода. Попутно можно заметить, что есть вертикальная асимптота с уравнением 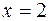 . Нанесите эту точку на координатную плоскость, покажите поведение функции вблизи асимптоты.
. Нанесите эту точку на координатную плоскость, покажите поведение функции вблизи асимптоты.
3. Функция не является ни четной, ни нечетной, ни периодической.
4. При 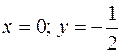 , а при
, а при 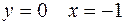 .
.
Точки пересечения с осями координат 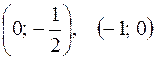 .
.
(Нанесите их на координатную плоскость).
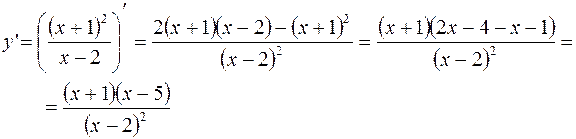
Критические точки 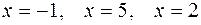 ; последняя является точкой разрыва.
; последняя является точкой разрыва.
5. Проверим выполнение достаточных условий:
Таблица
 | 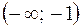 | -1 | 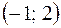 | 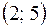 | 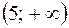 | ||
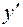 | + | - | не сущ. | - | + | ||
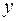 | возр. | max | убыв. | не сущ. | убыв. | min | возр. |
6. 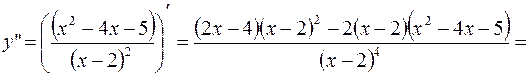

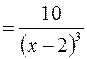
Вторая производная в ноль не обращается, не существует при 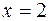 . Но это точка разрыва, следовательно, критических точек второго рода нет, точек перегиба нет.
. Но это точка разрыва, следовательно, критических точек второго рода нет, точек перегиба нет.
Найдем интервалы выпуклости, вогнутости.
Таблица
 | 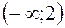 | 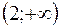 |
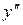 | - | + |
 | выпукла | вогнута |
7. Вертикальная асимптота уже определена, найдем наклонную:
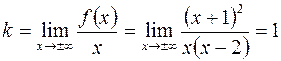
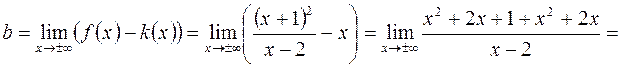
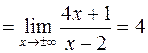 .
.
Следовательно, наклонная асимптота есть, ее уравнение 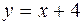 .
.
8. Используя полученные данные, строим график:
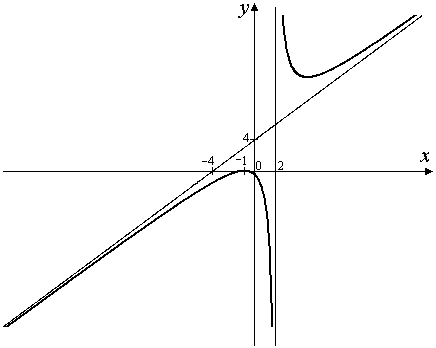 |
Решение 3) 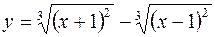
1. Функция определена на всей числовой оси.
2. Точек разрыва нет.
3. Функция нечетная, так как
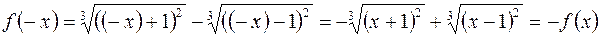 ,
,
её график симметричен относительно начала координат.
4. При 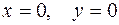 и при
и при 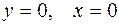 .
.
График функции проходит через начало координат.
5. 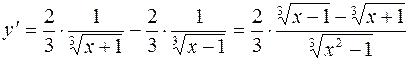
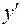 не обращается в ноль, но не существует в точках
не обращается в ноль, но не существует в точках 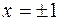 , которые и являются критическими.
, которые и являются критическими. 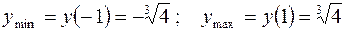 .
.
Таблица
 | 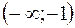 | – 1 | 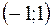 | 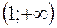 | |
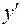 | - | 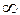 | + | 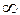 | - |
6. 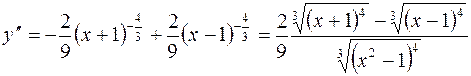 .
.
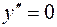 при
при 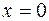 ,
, 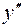 не существует в точках
не существует в точках 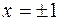 .
.
Проверяем выполнение достаточных условий:
Таблица
 | 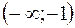 | – 1 | 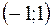 | 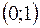 | 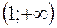 | ||
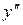 | - | 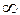 | - | + | 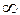 | + | |
 | выпукл. | нет перегиба | выпукл. | перегиб | вогнут. | нет перегиба | вогнут. |
Точка перегиба 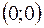 .
.
7. Вертикальной асимптоты нет, найдем наклонную асимптоту
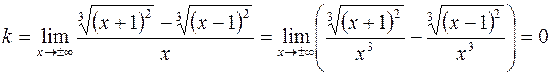 ;
;
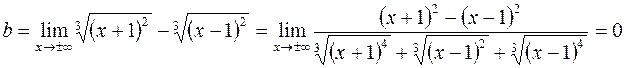
Следовательно, уравнение наклонной асимптоты 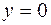 .
.
8. Строим график
|
Решение 4) 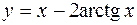 .
.
1. Функция определена на всей числовой оси.
2. Функция непрерывна на всей числовой оси.
3. Функция не является ни четной, ни нечетной, ни периодической.
4. 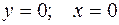 .
.
5. 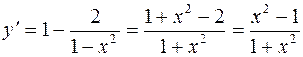 .
.
Критические точки 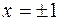 .
.
Таблица
 | 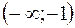 | – 1 | 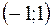 | 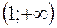 | |
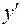 | + | – | + | ||
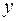 | возр. | убыв. | возр. |
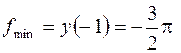 .
.
6. 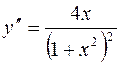 .
.
Критическая точка второго рода 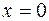 .
.
Таблица
 | 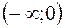 | 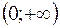 | |
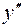 | – | + | |
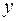 | выпукл. | перегиб | вогнут. |
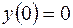 , точка перегиба
, точка перегиба 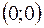 .
.
7. Вертикальных асимптот нет, найдем наклонную:
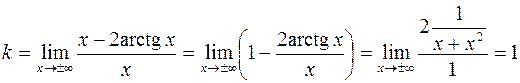 .
.
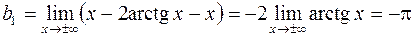 ;
;
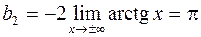 .
.
График функции имеет две наклонные асимптоты:
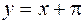 – левая и
– левая и 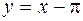 – правая.
– правая.
8. Строим график
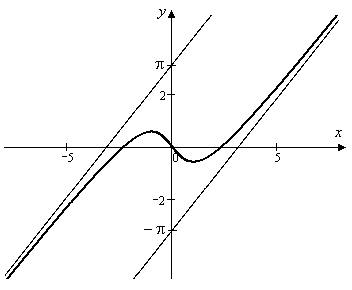 |
Применение логарифмической производной при дифференцировании некоторых функций.
Рассмотрим функцию такого вида:
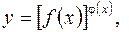 или
или 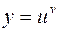 .
.
где 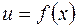 и
и 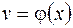 – дифференцируемые функции. Эту функцию нельзя дифференцировать как степень, так как показатель
– дифференцируемые функции. Эту функцию нельзя дифференцировать как степень, так как показатель 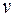 – не постоянная величина, а переменная, зависящая от
– не постоянная величина, а переменная, зависящая от  ; но нельзя эту функцию дифференцировать и как показательную функцию, так как основание
; но нельзя эту функцию дифференцировать и как показательную функцию, так как основание 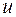 – не постоянная величина; функция эта сложная. Производную ее мы найдем, предварительно логарифмируя обе части равенства:
– не постоянная величина; функция эта сложная. Производную ее мы найдем, предварительно логарифмируя обе части равенства:
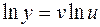 .
.
Производные обеих частей этого равенства равны между собой при этом 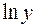 и
и 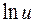 дифференцируются как функции от функции.
дифференцируются как функции от функции.
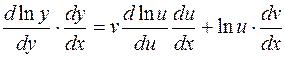 .
.
или
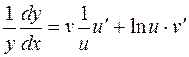 , откуда
, откуда
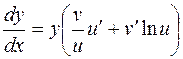 или
или 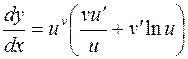 .
.
Пример. Рассмотрим наиболее простую из этого рода сложных функций
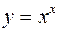 .
.
Логарифмируем обе части равенства и дифференцируем по  :
:
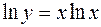 ;
; 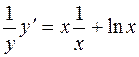 ;
;
откуда
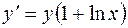 , или
, или 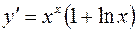 .
.
Таблица основных формул дифференциального исчисления
| № | Функция | Дифференциал |
| 1. | 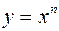 | 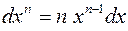 |
| 2. | 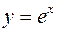 | 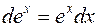 |
| 3. | 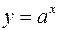 | 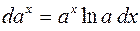 |
| 4. | 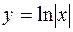 | 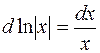 |
| 5. | 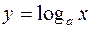 | 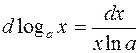 |
| 6. | 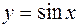 | 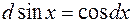 |
| 7. | 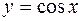 | 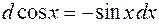 |
| 8. | 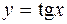 | 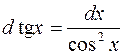 |
| 9. | 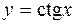 | 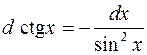 |
| 10. | 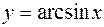 | 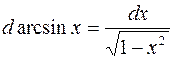 |
| 11. | 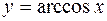 | 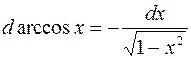 |
| 12. | 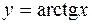 | 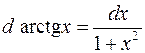 |
| 13. | 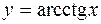 | 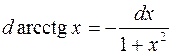 |
ВАРИАНТЫ РАСЧЕТНО – ГРАФИЧЕСКОЙ РАБОТЫ ПО ТЕМЕ
«ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ И ЕГО ПРИЛОЖЕНИЕ»
I, II – найти 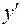 .
.
III – найти 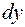 .
.
IV – написать уравнение касательной к кривой 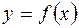 в точке
в точке 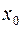 .
.
V – исследовать и построить график кривой.
Вариант1
I.
1. 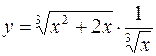 2.
2. 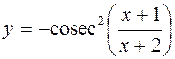
3. 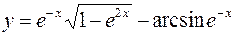 4.
4. 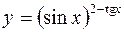
5. 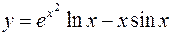 6.
6. 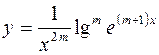
7. 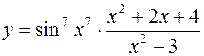 8.
8. 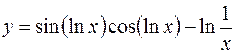
9. 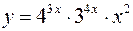
II.
1. 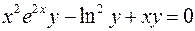 2.
2. 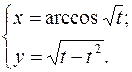
III.
1. 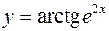 2.
2. 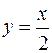
IV.
1. 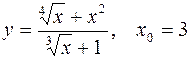
V.
1. 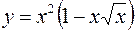
Вариант 2
I.
1. 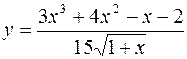 2.
2. 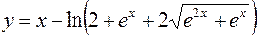
3. 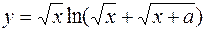 4.
4. 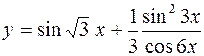
5. 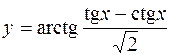 6.
6. 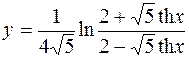
7. 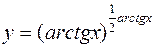
8. 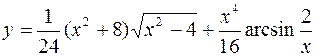 , (х> 0)
, (х> 0)
9. 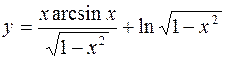 10.
10. 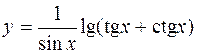
II.
1. 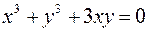 2.
2. 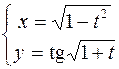
III.
1. 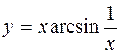 2.
2. 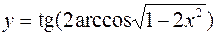
IV.
1. 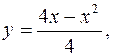
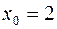
V.
1. 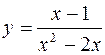
Вариант 3
I.
1. 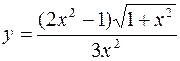 2.
2. 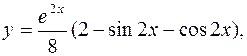
3. 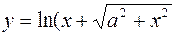 4.
4. 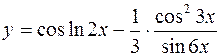 ,
,
5. 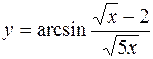 6.
6. 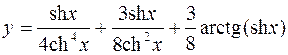
7. 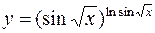
8. 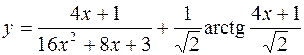
9. 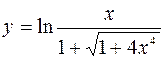 10.
10. 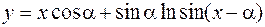
II.
1. 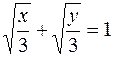 2.
2. 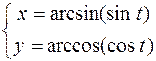
III.
1. 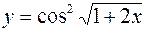 2.
2. 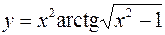
IV.
1. 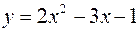 ,
, 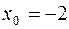
V.
1. 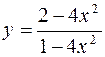 .
.
Вариант 4
I.
1. 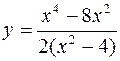 2.
2. 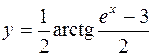
3. 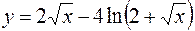 4.
4. 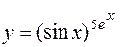
5. 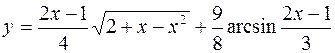
6. 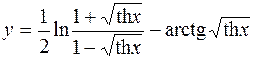
7. 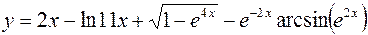
8. 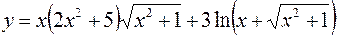
9. 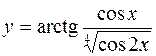 10.
10. 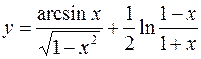
II.
1. 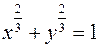 2.
2. 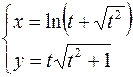
III.
1. 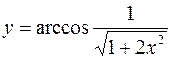 2.
2. 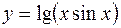
IV.
1. 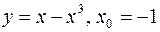
V.
1. 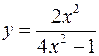
Вариант 5
I.
1. 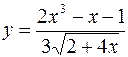 2.
2. 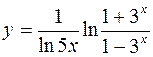
3. 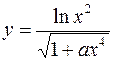 4.
4. 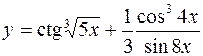
5. 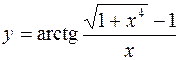 6.
6. 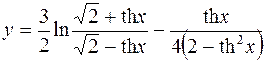
7. 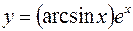
8. 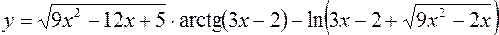
9. 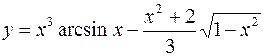 10.
10. 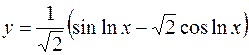
II.
1. 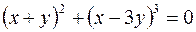 2.
2. 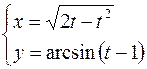
III.
1. 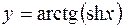 2.
2. 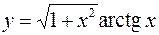
VI.
1. 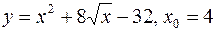
V.
1. 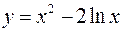
Вариант 6
I.
1. 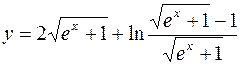 2.
2. 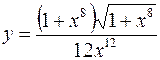
3. 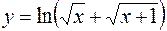 4.
4. 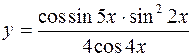
5. 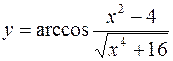 6.
6. 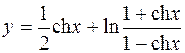
7. 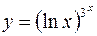 8.
8. 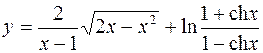
9. 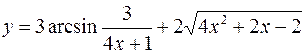
10. 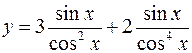
II.
1. 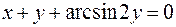 2.
2. 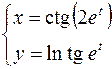
III.
1. 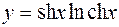 2.
2. 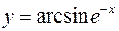
IV.
1. 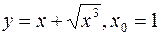
V.
1. 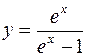
Вариант 7
I.
1. 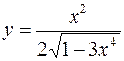 2.
2. 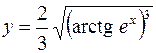
3. 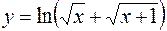

 4.
4. 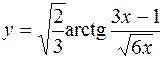
5. 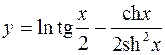 6.
6. 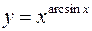
7. 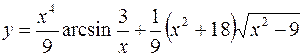
8. 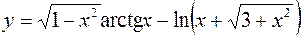
9. 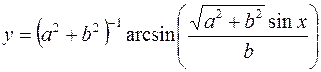
10. 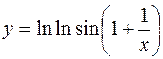
II.
1. 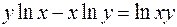 2.
2. 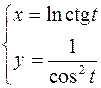
III.
1. 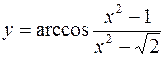 2.
2. 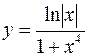
IV.
1. 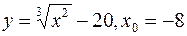
V.
1. 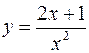
Вариант 8
I.
1. 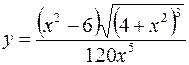 2.
2. 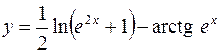
3. 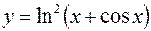 4.
4. 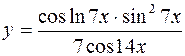
5. 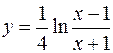 6.
6. 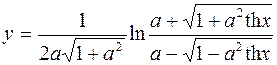
7. 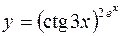 8.
8. 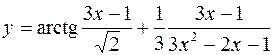
9. 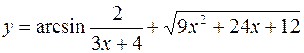
10. 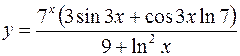
II.
1. 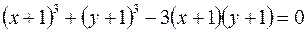
2. 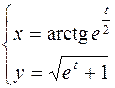
III.
1. 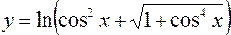 2.
2. 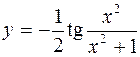
VI.
1. 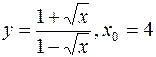
V.
1. 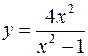
Вариант 9
I.
1. 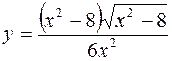 2.
2. 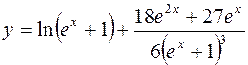
3. 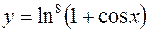 4.
4. 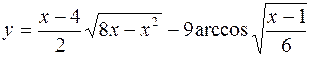
5. 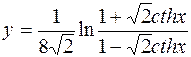 6.
6. 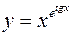
7. 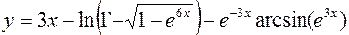
8. 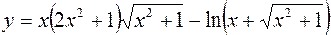
9. 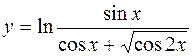 10.
10. 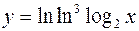
II.
1. 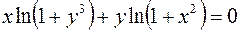 2.
2. 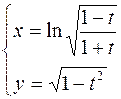
III.
1. 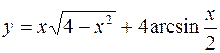 2.
2. 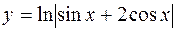
IV.
1. 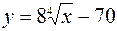 ,
, 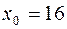
V.
1. 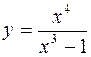
Вариант 10
I.
1. 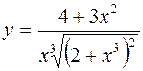 2.
2. 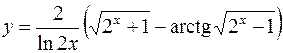
3. 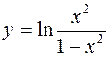 4.
4. 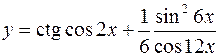
5. 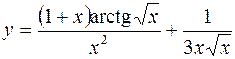 6.
6. 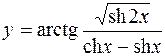
7. 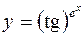
8. 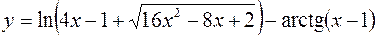
9. 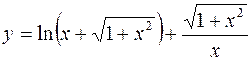
10. 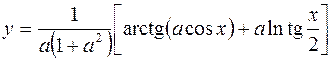
II.
1. 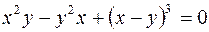 2.
2. 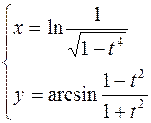
III.
1. 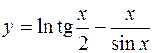 2.
2. 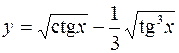
IV.
1. 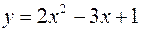 ,
, 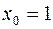
V.
1. 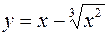
Вариант 11
I.
1. 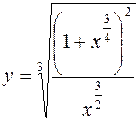 2.
2. 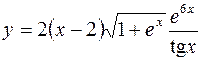
3. 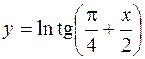 4.
4. 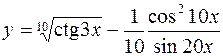
5. 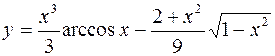 6.
6. 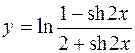
7. 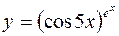 8.
8. 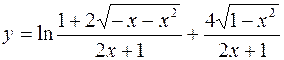
9. 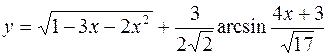
10. 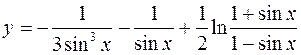
II.
1. 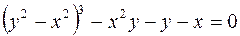 2.
2. 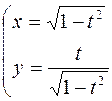
III.
1. 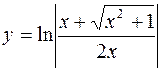 2.
2. 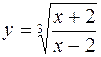
IV.
1. 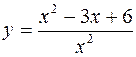 ,
, 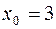
V.
1. 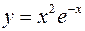
Вариант 12
I.
1. 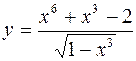 2.
2. 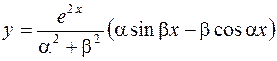
3. 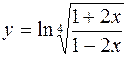 4.
4. 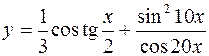
5. 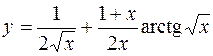 6.
6. 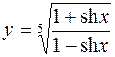
7. 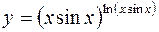
8. 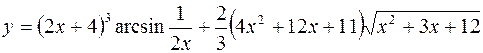
9. 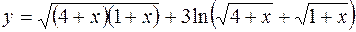
10. 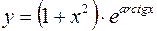
II.
1. 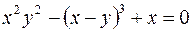
2. 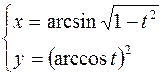
III.
1. 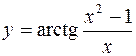 2.
2. 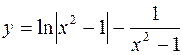
IV.
1. 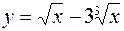 ,
, 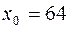
V.
1. 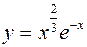
Вариант 13
I.
1. 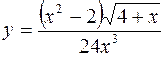 2.
2. 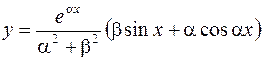
3. 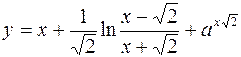 4.
4. 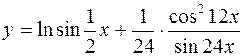
5. 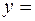
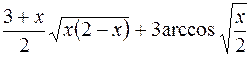 6.
6. 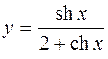
7. 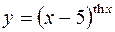 8.
8. 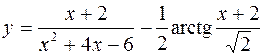
9. 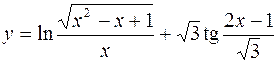 10.
10. 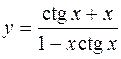
II.
1. 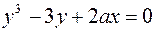 2.
2. 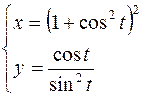
III.
1. 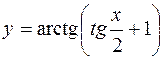 2.
2. 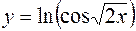
IV.
1. 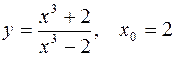
V.
1. 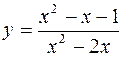
Вариант 14
I.
1. 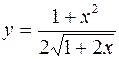 2.
2. 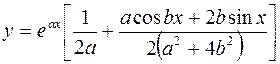
3. 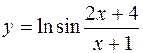 4.
4. 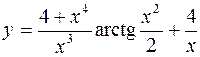
5. 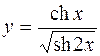 6.
6. 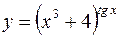
7. 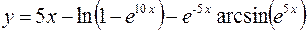
8. 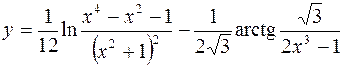
9. 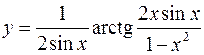 10.
10. 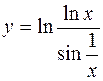
II.
1. 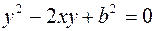 2.
2. 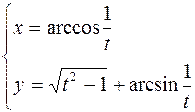
III.
1. 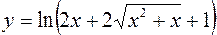 2.
2. 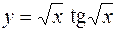
IV.
1. 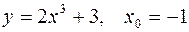
V.
1. 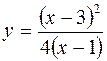
Вариант 15
I.
1. 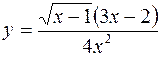 2.
2. 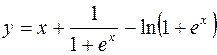
3. 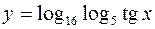 4.
4. 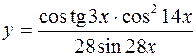
5. 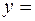
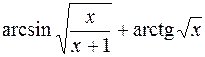 6.
6. 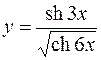
7. 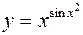
8. 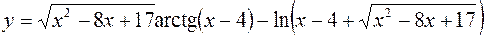
9. 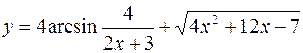
10. 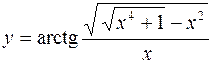
II.
1. 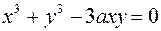 2.
2. 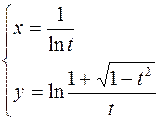
III.
1. 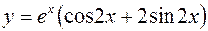 2.
2. 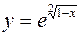
IV.
1. 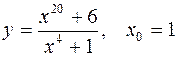
V.
1. 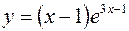
Вариант 16
I.
1. 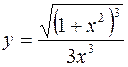
2. 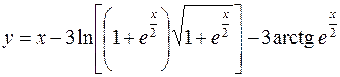
3. 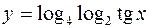 4.
4. 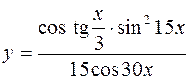
5. 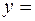
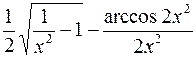 6.
6. 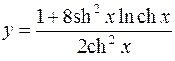
7. 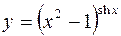
8. 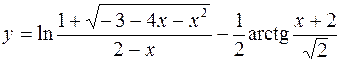
9. 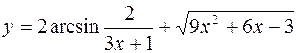
10. 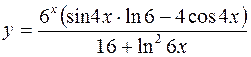
II.
1. 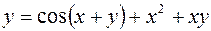 2.
2. 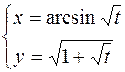
III.
1. 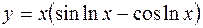 2.
2. 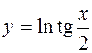
IV.
1. 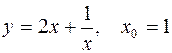
V.
1. 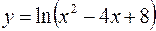
Вариант 17
I.
1. 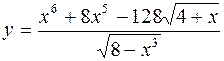 2.
2. 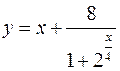
3. 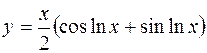 4.
4. 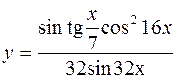
5. 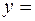
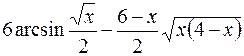 6.
6. 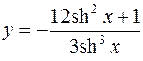
7. 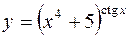 8.
8. 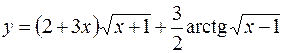
9. 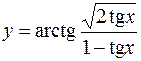
10. 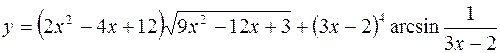
II.
1. 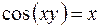 2.
2. 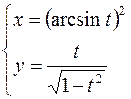
III.
1. 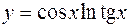 2.
2. 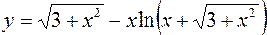
IV.
1. 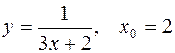
V.
1. 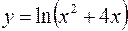
Вариант 18
I.
1. 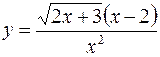 2.
2. 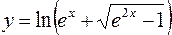
3. 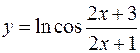 4.
4. 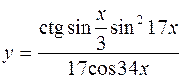
5. 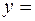
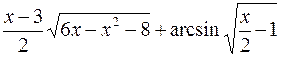
6. 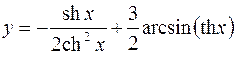
7. 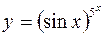 8.
8. 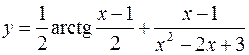
9. 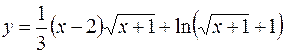 10.
10. 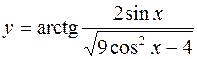
II.
1. 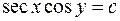 2.
2. 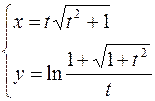
III.
1. 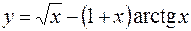 2.
2. 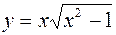
IV.
1. 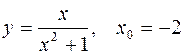
V.
1. 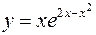
Вариант 19
I.
1. 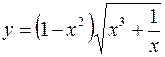
2. 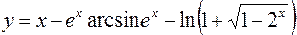
3. 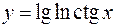 4.
4. 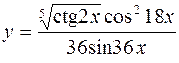
5. 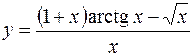 6.
6. 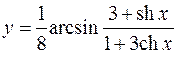
7. 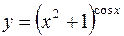
8. 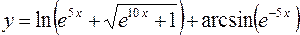
9. 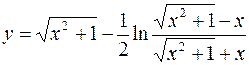 10.
10. 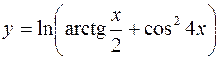
II.
1. 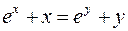 2.
2. 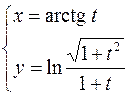
III.
1. 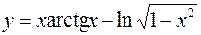 2.
2. 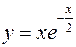
IV.
1. 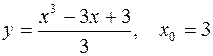
V.
1. 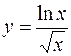
Вариант 20
I.
1. 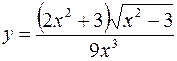 2.
2. 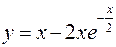
3. 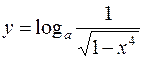 4.
4. 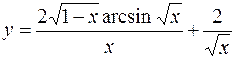
5. 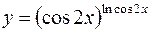 6.
6. 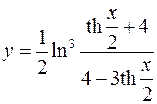
7. 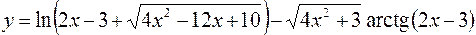
8. 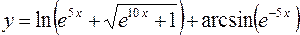
9. 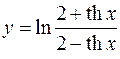 10.
10. 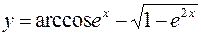
II.
1. 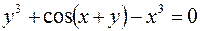 2.
2. 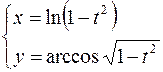
III.
1. 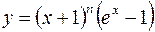 2.
2. 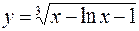
IV.
1. 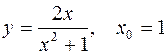
V.
1. 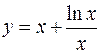
Вариант 21
I.
1. 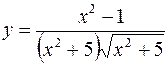 2.
2. 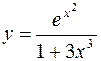 ,
,
3. 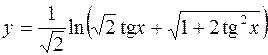 4.
4. 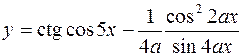
5. 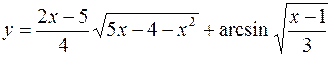
6. 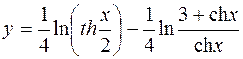
7. 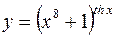
8. 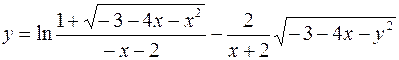
9. 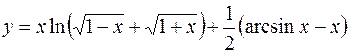
10. 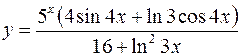
II.
1.
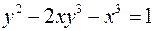 2.
2.
|
|
 2015-10-22
2015-10-22 1941
1941