Платежная матрица игры

таблица 2

B j A i	B 1	B 2	B 3	B 4	a i
A 1
A 2
A 3
A 4					10
b j			8

Применяя принцип максимина, находим в добавочном столбце a _i наилучшее значение (в нашем случае наибольшее значения) - a = 10. В добавочной нижней строке b_j, применяя принцип минимакса, также находим наилучшее значение для игрока В (в нашем случае наименьшее значение) - b = 8. Седловая точка в данной матрице отсутствует, т.к.

Следовательно, решение игры возможно только в смешанных стратегиях. Важным свойством оптимальной смешанной стратегии является то, что при любой стратегии противника (чистой или смешанной) она обеспечивает игроку средний выигрыш не меньше, чем в случае применения противником его оптимальной стратегии.

Прежде, чем определять пару оптимальных смешанных стратегий игроков (S_A, S_B) пoпытаемся путем анализа доминирования стратегий свести игру к игре с меньшим количеством стратегий. Стратегия А₁ доминирует над стратегией А₃, поэтому отбросим ее; стратегия В₂ доминирует над стратегией В₁ и В₄ - отбросим их; стратегия А₂ доминирует над стратегией А₁ - отбросим ее. В таблице 2 выделены стратегии, которые отбрасываются. В результате получаем матрицу типа 2х2 (таблица 3).

Используя известные зависимости определим вероятности p и q для игроков:

Платежная матрица

таблица 3

B j A i	B 2	B 3
A 2
A 4

Итак, технолог должен с вероятностью 0,25 применять технологию А₂, с вероятностью 0,75 применять технологию А₄ и совсем не применять технологии А₁ и А₃, т.е. чередовать технологии следующим образом: на три раза использования технологи А_{4 ,} один раз применять технологию А₂ и так далее. При этом величина среднего платежа для А₂ составляет: ;

для А₄ составляет .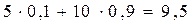

В случае, когда не удается уменьшить количество стратегий вплоть до размера 2х2, тогда необходимо для определения оптимальной пары стратегий (S_A, S_B) применять метод итераций.

Сходимость метода итераций довольно медленная: точность, сравнимая с численными методами, начинается при количестве итераций более 30. При уменьшении исходной матрицы трудоемкость расчетов существенно снижается.

Следующим этапом в теории игр является оценка выбора решений с помощью критериев Вальда, Сэвиджа и Гурвица.

Максиминный критерий Вальда гарантирует выигрыш в любом случае не меньший, чем нижняя цены игры α:

Критерий минимаксного риска Сэвиджа предлагает выбрать ту стратегию, при которой величина риска в наихудших условиях минимальна:

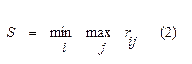
Чтобы получить риск r_ij нужно из В_j вычесть фактический выигрыш а_ij:

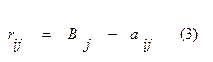
Критерий пессимизма- оптимизма Гурвица предлагает выбрать стратегию, которая удовлетворяет условию:

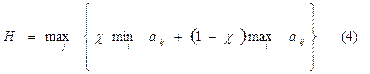
где χ - коэффициент "пессимизма".

При χ = 1 критерий Гурвица превращается в критерий Вальда, при χ = 0 - в критерий «крайнего оптимизма».

Следующим этапом работы является нахождение оптимальных стратегий с использованием пакета «Поиск решения».