Рассмотрим электрическое и магнитное поля в однородной непроводящей среде: 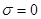 Þ
Þ 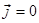 ,
, 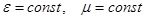 .
.
Пусть в этой среде отсутствуют объемные заряды, т.е. 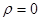 .
.
Уравнения Максвелла (с учетом материальных уравнений) будут иметь вид:
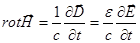 (1)
(1)
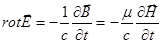 (2)
(2)
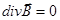 Þ
Þ 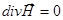 (3)
(3)
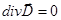 Þ
Þ 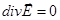 (4).
(4).
Применим операцию 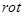 к уравнению (1):
к уравнению (1):
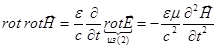 ;
;
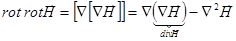 .
.
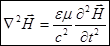 (*).
(*).
Применим операцию 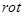 к уравнению (2):
к уравнению (2):
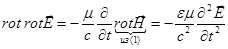 ,
,
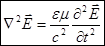 (**).
(**).
(*) и (**) – волновые уравнения. Это известно из математики и мы чуть позже это покажем.
Итак, магнитный вектор 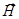 и вектор напряженности электрического поля
и вектор напряженности электрического поля 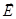 удовлетворяют одному и тому же уравнению вида:
удовлетворяют одному и тому же уравнению вида:
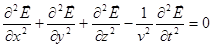 ,
, 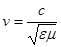 - скорость распространения волны.
- скорость распространения волны.
В вакууме 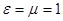 и скорость распространения электромагнитной волны равна
и скорость распространения электромагнитной волны равна 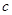 - скорости света.
- скорости света.
Электромагнитные поля, существующие в вакууме в отсутствие зарядов и токов, называются электромагнитными волнами.
Электромагнитные поля в вакууме обязательно должны быть переменными. Мы уже убедились, что
при 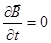 , что в вакууме соответствует
, что в вакууме соответствует 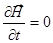 , и
, и
при 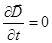 , что в вакууме соответствует
, что в вакууме соответствует 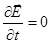 ,
,
уравнения Максвелла распадаются на независимые уравнения
- электростатики: 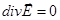 ,
, 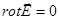 ;
;
- магнитостатики: 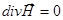 ,
, 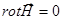 ,
,
которые не имеют никаких решений, кроме тривиальных 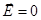 ,
, 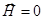 . Следовательно, статических полей в вакууме (в отсутствие зарядов и токов, и именно это означает слово «вакуум») быть не может.
. Следовательно, статических полей в вакууме (в отсутствие зарядов и токов, и именно это означает слово «вакуум») быть не может.
Волновое уравнение для потенциала
В вакууме:  (т.к.
(т.к. 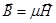 ).
).
Отсюда: 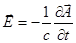 .
.
Берем уравнение (1): 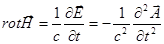 .
.
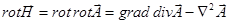 .
.
Будем так выбирать вектор-потенциал, чтобы 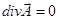 .
.
Получаем: 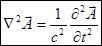 .
.
Записывают это уравнение еще и так
ˆ 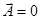 - уравнение д’Аламбера.
- уравнение д’Аламбера.
ˆ 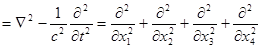 , где
, где 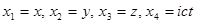 .
.
Итак, мы установили, что переменные магнитные поля даже в вакууме порождают электрические поля, а переменные электрические поля даже в вакууме порождают магнитные поля.
Уравнения Максвелла (с учетом материальных уравнений) приводят к волновым уравнениям для электрического и магнитного векторов
(стандартный вид волнового уравнения 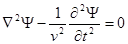 ,
, 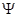 - волновая функция)
- волновая функция)
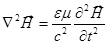 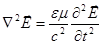 | Здесь 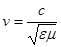 - скорость распространения волны. - скорость распространения волны. 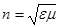 - показатель преломления среды. - показатель преломления среды. |
Электромагнитные поля, существующие в вакууме в отсутствие зарядов и токов, называются электромагнитными волнами.
Статических полей в вакууме существовать не может (в этом случае уравнения Максвелла дают тривиальные, т. е. нулевые решения).
Плоские волны
Пусть поле зависит от одной какой-нибудь координаты. Волновое уравнение в вакууме имеет вид:
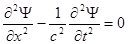 , где
, где 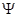 - любая компонента векторов
- любая компонента векторов 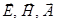 .
.
Умножаем правую и левую части на 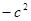 :
:
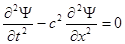 .
.
Рассмотрим оператор 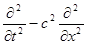 .
.
Волновое уравнение можно представить в виде:
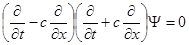 .
.
Введем новые переменные:
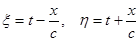 .
.
Их сумма: 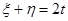 ; Þ
; Þ 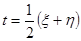 .
.
Разность: 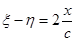 ; Þ
; Þ 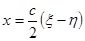 .
.
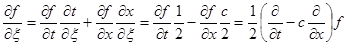 .
.
Аналогично
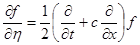 .
.
Отсюда видно, что уравнение (одномерное волновое уравнение)
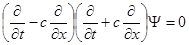 в новых переменных имеет вид:
в новых переменных имеет вид:
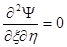 .
.
Решением этого уравнения является функция 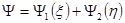 , где
, где 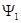 и
и 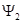 - некоторые произвольные функции.
- некоторые произвольные функции.
Делая обратную замену переменных, находим:
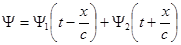 .
.
Допустим 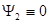 , тогда
, тогда 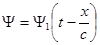 .
.
В плоскости 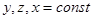 поле
поле 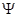 зависит от времени.
зависит от времени.
В момент времени 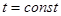 (фиксированный момент времени, моментальная фотография, «остановись, мгновенье!») поле
(фиксированный момент времени, моментальная фотография, «остановись, мгновенье!») поле 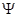 зависит от координаты
зависит от координаты 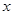 .
.
Поле 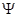 имеет одинаковое значение для координат
имеет одинаковое значение для координат 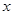 и моментов времени
и моментов времени 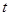 , удовлетворяющих условию
, удовлетворяющих условию
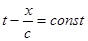 , или
, или 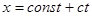 (поле распространяется по направлению положительной оси
(поле распространяется по направлению положительной оси 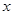 со скоростью
со скоростью 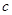 ).
).
Отсюда: 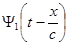 - это плоская - волна, распространяющаяся по положительному направлению оси
- это плоская - волна, распространяющаяся по положительному направлению оси 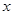 . (Плоская – так как в любой точке плоскости
. (Плоская – так как в любой точке плоскости 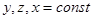 в момент времени
в момент времени 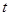 она имеет одинаковые значения.)
она имеет одинаковые значения.)
Аналогичными рассуждениями приходим к заключению, что 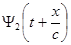 - это плоская волна, распространяющаяся по отрицательному направлению оси
- это плоская волна, распространяющаяся по отрицательному направлению оси 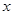 .
.
Поперечность электромагнитной волны
Потенциалы выбираем так, чтобы 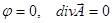 .
.
Последнее условие для нашего одномерного случая имеет вид 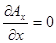 .
.
В волновом уравнении, полагая 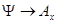 (замена), имеем:
(замена), имеем:
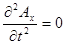 Þ
Þ 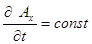 .
.
Теперь вспомним, что 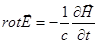 ,
,
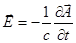 .
.
В нашем одномерном случае:
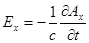 Þ
Þ 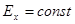 .
.
В вакууме 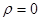 ; следовательно, постоянного электрического поля быть не может, поэтому единственное возможное значение
; следовательно, постоянного электрического поля быть не может, поэтому единственное возможное значение 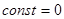 и
и 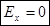 .
.
Вывод:
электрическое поле в электромагнитной волне не может иметь компоненту, направленную вдоль распространения волны, а может лишь в перпендикулярных направлениях.
Что касается магнитного поля, то 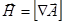 .
.
Мы рассматриваем электромагнитную волну, распространяющуюся в положительном направлении оси 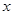 , т.е.
, т.е. 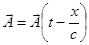 {в этой волне все величины зависят только от
{в этой волне все величины зависят только от 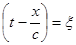 }.
}.
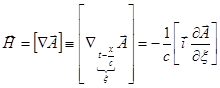 .
.
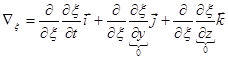 ;
; 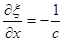 .
.
Электрическое поле: 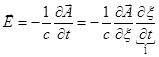 .
.
Поскольку мы получили 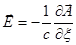 , то
, то 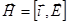 .
.
В электромагнитной волне электрический и магнитный векторы перпендикулярны друг другу и направлению распространения волны.
Поперечность электромагнитной волны – одно из главных ее свойств.
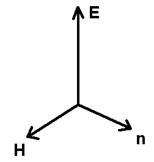 |
РИС.23-1
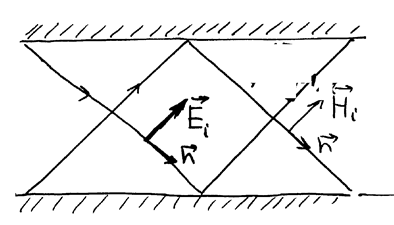 |
Пусть электромагнитная волна распространяется между двумя параллельными отражающими пластинками (упрощенная модель волновода). При этом волны (входящие под углом) отражаются от ограничивающих плоскостей. Ось z-вдоль волновода.
РИС.23-2
Каждая волна, конечно, строго поперечна (по отношению к вектору распространения 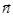 ).
).
Однако, в волне, распространяющейся вдоль оси 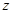 и мало отличающейся от свободной волны, будут составляющие векторов
и мало отличающейся от свободной волны, будут составляющие векторов 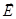 и
и 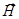 вдоль оси
вдоль оси 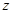 . Эта составляющая определяется путем суммирования компонент
. Эта составляющая определяется путем суммирования компонент 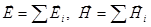 . - это результирующие напряженности. В зависимости от конкретных условий распространения волны в волноводе могут появиться компоненты как
. - это результирующие напряженности. В зависимости от конкретных условий распространения волны в волноводе могут появиться компоненты как 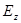 , так и
, так и 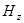 . Мы будем рассматривать свободные волны, но при отражении и преломлении свободных волн может возникать составляющая
. Мы будем рассматривать свободные волны, но при отражении и преломлении свободных волн может возникать составляющая 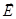 в направлении распространения волны.
в направлении распространения волны.
 |
Поляризация электромагнитной волны
РИС.23-3
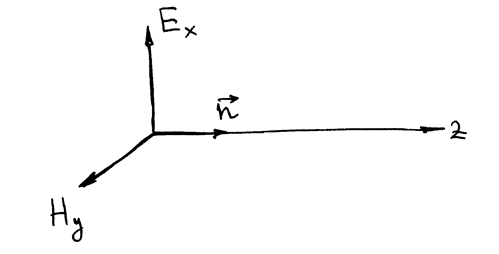
Вектора 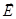 и
и 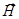 взаимно перпендикулярны и перпендикулярны
взаимно перпендикулярны и перпендикулярны 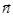 - направлению распространения свободной электромагнитной волны. Сказанное справедливо во все моменты времени. Однако плоскость, в которой находится вектор
- направлению распространения свободной электромагнитной волны. Сказанное справедливо во все моменты времени. Однако плоскость, в которой находится вектор 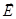 (или
(или 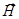 ), от одного момента к другому меняется произвольным образом, так что все направления в плоскости
), от одного момента к другому меняется произвольным образом, так что все направления в плоскости 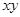 равноправны и в среднем по времени вектора
равноправны и в среднем по времени вектора 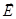 (равно как и вектора
(равно как и вектора 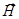 ) расположены вполне симметрично относительно направления распространения волны.
) расположены вполне симметрично относительно направления распространения волны.
Неполяризованная, естественная волна:
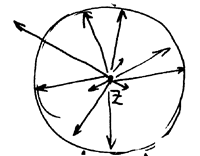 |
РИС.23-4
Бывают ситуации, когда вектора 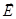 и
и 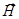 сохраняют свое пространственное положение, совершая, например, колебания в одной какой-либо плоскости.
сохраняют свое пространственное положение, совершая, например, колебания в одной какой-либо плоскости.
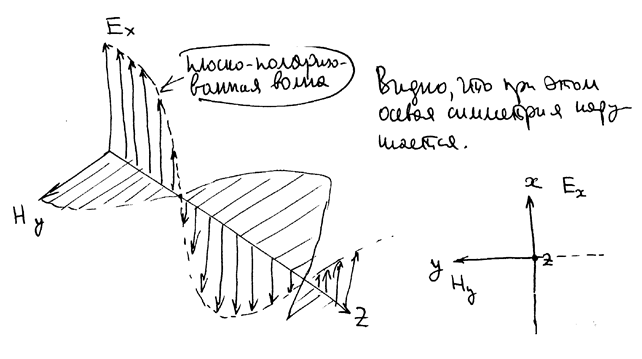
РИС.23-5
Поляризацией волны называется нарушение осевой симметрии относительно направления распространения волны в поперечной волне, выражающееся в том, что величины смещений и скоростей в механической волне или напряженностей электрического и магнитного поля в электромагнитной волне (вообще – смещений) в разных направлениях, лежащих в плоскости, перпендикулярной к направлению распространения волны 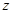 , оказываются различными.
, оказываются различными.
Причины возникновения поляризации:
- отсутствие осевой симметрии в излучателе,
- распространение волны в анизотропной среде,
- преломление и отражение волны на границе двух сред.
Чтобы обнаружить поляризацию электромагнитных волн, нужно измерять величины смещений в различных направлениях, перпендикулярных к направлению распространения волны. Безинерционные приборы будут измерять мгновенные значения смещений, приборы с большой инерцией измеряют среднеквадратичное смещение.
Характер поляризации определяется тем, как связаны между собой значения смещений (мгновенные или среднеквадратичные) для различных направлений, лежащих в плоскости, перпендикулярной направлению распространения волны.
 |
В предельно асимметричном случае, когда направление смещения все время лежит в одной и той же плоскости, проходящей через направление распространения волны, во всех других направлениях смещение равно нулю. В этом случае волна называется плоско-поляризованной, а плоскость, в которой лежат смещения, называется плоскостью поляризации.
РИС.23-6
При распространении волны плоскость ее поляризации может не оставаться неподвижной, т.е. волна может менять свою ориентацию относительно направления распространения. Например, часто возникает такое колебание, что конец вектора 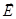 (и ортогонального ему вектора
(и ортогонального ему вектора 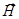 ) движется по эллипсу: эллиптическая поляризация. Частным случаем ее является круговая поляризация (циркулярно право - и лево - поляризованный свет); непосредственно наблюдать циркулярную поляризацию невозможно.
) движется по эллипсу: эллиптическая поляризация. Частным случаем ее является круговая поляризация (циркулярно право - и лево - поляризованный свет); непосредственно наблюдать циркулярную поляризацию невозможно.
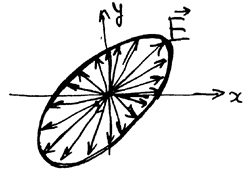 |
РИС.23-7
Эллипс может выродиться в прямую – это плоская (линейная) поляризация. Следовательно, эллиптическая поляризация является наиболее общим случаем поляризации электромагнитных волн.
Поток энергии в электромагнитной волне
В среде с 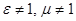 энергия электромагнитного поля:
энергия электромагнитного поля:
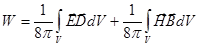 .
.
Такое выражение для электромагнитной энергии, вообще говоря, постулируется. Дело в том, что мы можем судить о существовании электромагнитного поля лишь по наблюдаемому нами возникновению или исчезновению (изменению) доступных нашему восприятию форм энергии (тепловой, механической и т.п.) - ведь нашему непосредственному восприятию доступна лишь малая часть спектра электромагнитных волн – световые волны в видимой части спектра.
Возникновение известных нам форм энергии должно происходить за счет какой-то иной, неизвестной нам формы, которую мы называем энергией электромагнитного поля. Приняв это выражение для электромагнитной энергии, мы получаем возможность проверить на опыте всю совокупность уравнений Максвелла.
Выражая электромагнитную энергию в форме объемного интеграла, мы получаем возможность истолковать это выражение так, что энергия определенным образом локализована в пространстве, и объемная плотность энергии определяется соотношением
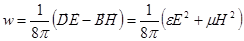 .
.
Рассмотрим изменение во времени количества энергии 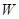 , находящегося внутри объема
, находящегося внутри объема 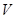 , ограниченного поверхностью
, ограниченного поверхностью 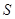 :
:
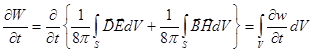 .
.
Ввиду предполагаемой независимости 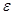 и
и 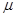 от времени, дифференцируя, имеем:
от времени, дифференцируя, имеем:
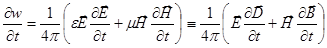 .
.
Вспоминаем, что
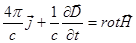 Þ
Þ 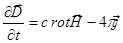 ;
;
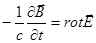 Þ
Þ 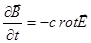 .
.
Подставляем:
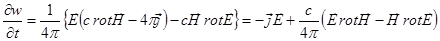 .
.
Математическое отступление.
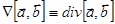 ;
;
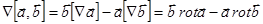 .
.
Следовательно, 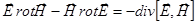 .
.
Итак: 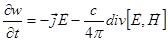 .
.
Отсюда:
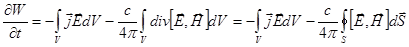 .
.
Если поверхность 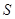 охватывает область полного поля (
охватывает область полного поля (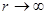 ), то
), то 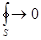 .
.
Если все находящиеся в поле тела неподвижны, то энергия поля расходуется только на работу электрического поля над токами проводимости (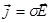 ):
):
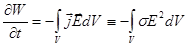 (расходуется на джоулево тепло -
(расходуется на джоулево тепло - 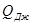 ).
).
Если среда непроводящая, 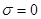 , то
, то
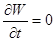 . Это закон сохранения энергии для электромагнитного поля.
. Это закон сохранения энергии для электромагнитного поля.
Рассмотрим теперь случай, когда поверхность 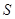 не охватывает область полного поля, т.е.
не охватывает область полного поля, т.е. 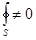 .
.
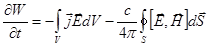 .
.
Введем вектор: 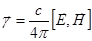 .
.
Закон сохранения энергии примет вид:
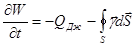 .
.
Электромагнитная энергия вытекает из рассматриваемого объема через его поверхность в количестве 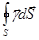 эрг/с. Это утверждение называется теоремой Пойнтинга, а вектор
эрг/с. Это утверждение называется теоремой Пойнтинга, а вектор 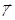 - вектором Умова-Пойнтинга.
- вектором Умова-Пойнтинга.
В каждой точке поля поток электромагнитной энергии (т.е. количество энергии, протекающее в единицу времени через перпендикулярную направлению потока единицу поверхности) равен по величине и направлению вектору Умова-Пойнтинга 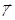 .
.
Отсюда, обращаясь к представлению об объемной плотности энергии, имеем:
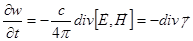 .
.
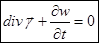 - уравнение непрерывности для плотности потока энергии.
- уравнение непрерывности для плотности потока энергии.
Поток энергии в плоской волне
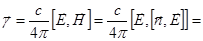 {правило «бац-цаб»:
{правило «бац-цаб»: 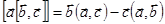 }
}
= 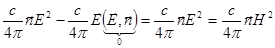 .
.
Направление потока энергии 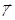 совпадает с направлением распространения электромагнитной волны
совпадает с направлением распространения электромагнитной волны 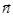 .
.
Поток энергии распространяется с той же скоростью, что и электромагнитная волна.
24 КОЛЕБАНИЯ И ВОЛНЫ
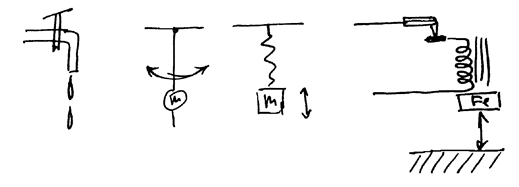 |
Примеры
РИС.24-1
Колебание – это такая форма движения, при которой параметры движения повторяются (или приблизительно повторяются) через равные (или приблизительно равные) промежутки времени.
Уравнение колебаний
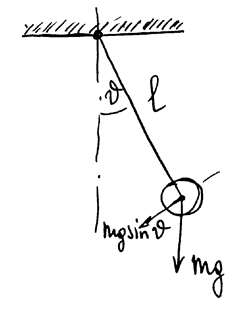 |
Физический маятник
РИС.24-2
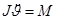 ,
, 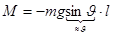 ,
,
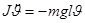 ,
, 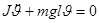 ;
;
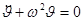 Þ
Þ 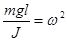 .
.
Математический маятник - невесомая нить без трения и деформации: 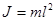 .
.
Уравнение движения: 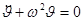 Þ
Þ 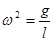 .
.
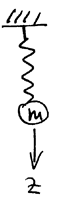 |
Пружинный маятник
РИС.24-3
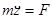 ,
,
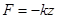 ,
,
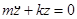 ,
,
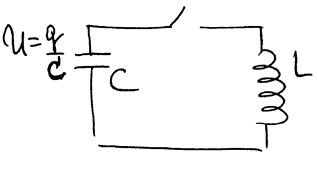 |
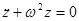 Þ
Þ 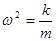 .
. РИС.24-4
Разность потенциалов между обкладками конденсатора должна быть равна э.д.с. самоиндукции.
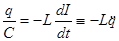 ,
,
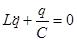 ,
,
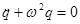 Þ
Þ 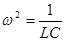 .
.
Общий вид уравнения движения: 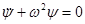 .
.
Общее решение: 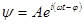 (
(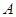 - амплитуда,
- амплитуда, 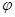 - начальная фаза).
- начальная фаза).
Гармонические незатухающие колебания:
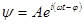 ,
,
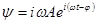 ,
,
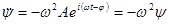 , т.е. удовлетворяет общему уравнению.
, т.е. удовлетворяет общему уравнению.
Амплитуда 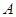 и начальная фаза
и начальная фаза 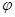 определяются из начальных и граничных условий задачи.
определяются из начальных и граничных условий задачи.
Пример для математического маятника
В начальный момент времени 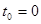 маятник отклонен на угол
маятник отклонен на угол 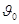 и отпущен без начального толчка,
и отпущен без начального толчка, 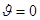 .
.
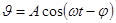 ;
;
при 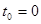
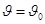 Þ
Þ 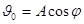 ;
;
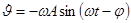 ,
,
при 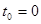
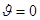 Þ
Þ 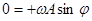 Þ
Þ 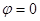 Þ
Þ 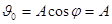 .
.
Закон движения:
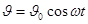 .
.
Период колебаний
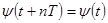 (
(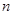 - целое число,
- целое число, 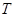 - период колебаний).
- период колебаний).
Для гармонических колебаний:
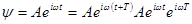 .
.
Значит, 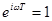 Þ
Þ 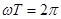 ;
;
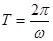 ,
, 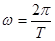 ,
, 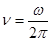 .
.
Сложение, или суперпозиция колебаний
Гармонические колебания с одинаковыми частотами (синхронные):
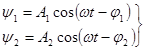 ищем
ищем 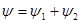 .
.
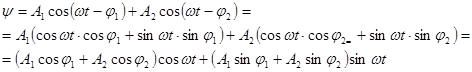
Покажем, что всегда можно найти такие действительные числа 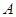 и
и 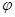 , чтобы
, чтобы
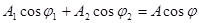 ,
,
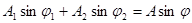 .
.
Возведем в квадрат и сложим:
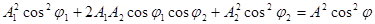 ,
,
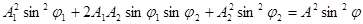 ,
,
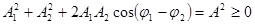 .
.
Теперь поделим второе на первое:
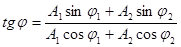 .
.
Теперь результат сложения колебаний стал:
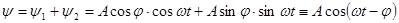 .
.
Суперпозиция двух гармонических колебаний одинаковой частоты есть гармоническое колебание той же частоты.
Его амплитуда 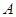 :
:
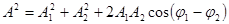 - зависит от разности начальных фаз исходных колебаний.
- зависит от разности начальных фаз исходных колебаний.
Частный случай 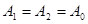 , тогда
, тогда
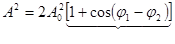 .
.
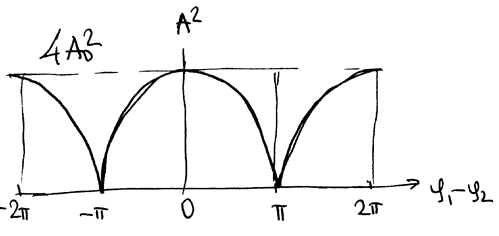 |
Функция в квадратных скобках меняется от 0, что соответствует
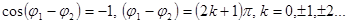 , до 2, что соответствует
, до 2, что соответствует 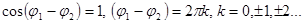
РИС.24-5
Практическое применение полученного результата для расчета цепей переменного тока
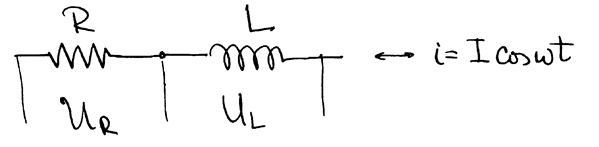 |
РИС.24-6
 ,
,
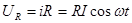 ,
,
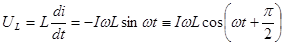 .
.
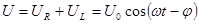 ,
,
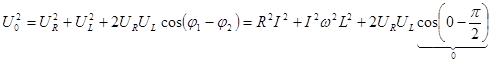 ,
,
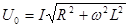 ,
,
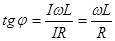 .
.
Суперпозиция (сложение) гармонических колебаний с близкими частотами
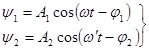
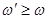 .
.
Обозначим 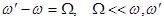 ,
,
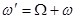 .
.
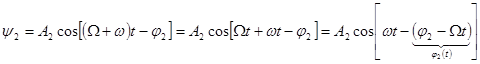 , где
, где 
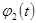 - медленно меняющаяся функция времени.
- медленно меняющаяся функция времени.
Далее воспользуемся формулами сложения синхронных колебаний:
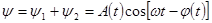 ,
,
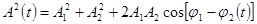 ,
,
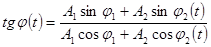 ,
,
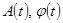 - медленно меняющиеся функции времени.
- медленно меняющиеся функции времени.
Получили колебания на частоте 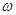 , но с зависящей от времени амплитудой.
, но с зависящей от времени амплитудой.
Математическое отступление
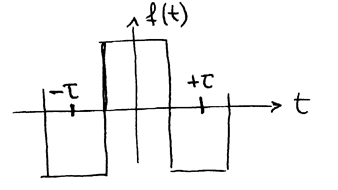 |
Теория суперпозиции колебаний есть часть общего математического подхода к описанию негармонических периодических и даже непериодических процессов: часть гармонического анализа.
РИС.24-7
Задана некоторая периодическая функция 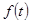 с периодом
с периодом 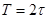 , имеющая на периоде не более конечного числа точек разрыва и абсолютно интегрируемая на этом сегменте.
, имеющая на периоде не более конечного числа точек разрыва и абсолютно интегрируемая на этом сегменте.
Эту функцию можно представить в виде:
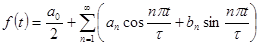 (это ряд Фурье),
(это ряд Фурье),
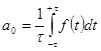 ,
,
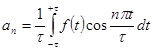 ,
,
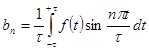 .
.
В комплексной форме:
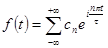 , где
, где 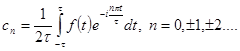
Любое сложное колебание представляет собой суперпозицию гармонических колебаний.
Вообще весьма широкий класс функций 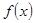 можно разложить в обобщенный ряд Фурье относительно ортонормированной системы функций
можно разложить в обобщенный ряд Фурье относительно ортонормированной системы функций 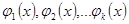 :
:
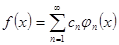 .
.
Окончание математического отсупления
Примеры
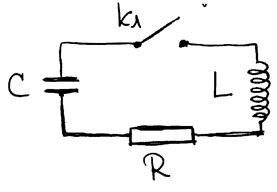 |
Колебательный контур с учетом сопротивления проводов.
РИС.24-8
Сумма всех напряжений в цепи должна быть равна нулю:
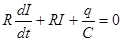 ,
,
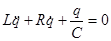 ,
,
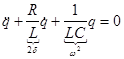 .
.
Уравнение затухающих колебаний:
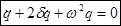 .
.
Демпфированная механическая система
Перекачка энергии из кинетической в потенциальную и обратно происходит с потерями. Часть энергии переходит в тепло и рассеивается.
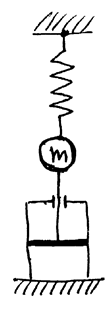 |
РИС.24-9
Общее решение:
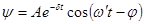 {
{ 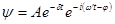 }
}
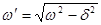 .
.
Это почти периодическое решение имеет смысл, если затухание не чрезмерно сильное: 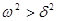 .
.
В случае сильного затухания, 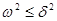 , получаем апериодическое решение.
, получаем апериодическое решение.
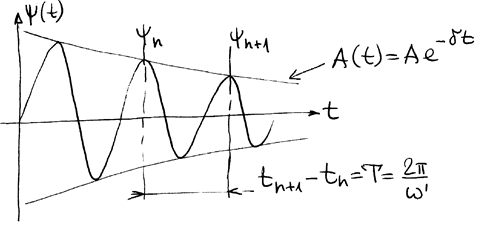 |
Это почти периодическое решение имеет смысл, если затухание не чрезмерно сильное:
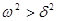 . В случае сильного затухания,
. В случае сильного затухания, 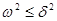 , получаем апериодическое решение.
, получаем апериодическое решение. РИС.24-10
Физический смысл затухания
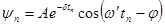 ,
,
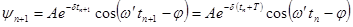 ,
,
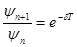 Þ
Þ 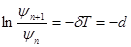 - логарифмический декремент затухания.
- логарифмический декремент затухания.
Логарифмический декремент затухания 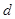 показывает, через сколько периодов амплитуда станет в
показывает, через сколько периодов амплитуда станет в 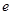 раз меньше.
раз меньше.
Была амплитуда: 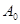 .
.
Через 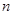 периодов:
периодов: 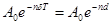 ,
,
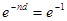 , т.е.
, т.е. 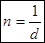 .
.
Величина, обратная логарифмическому декременту затухания, это есть число периодов, по истечении которых амплитуда затухающих колебаний уменьшится в 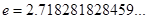
Примеры:
Хороший камертон имеет 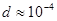 . Это значит, что амплитуда его колебаний уменьшится в
. Это значит, что амплитуда его колебаний уменьшится в 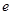 раз по истечении 10 000 периодов.
раз по истечении 10 000 периодов.
Затухание электрического контура 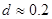 . Через 5 периодов амплитуда будет составлять 1/3 начальной.
. Через 5 периодов амплитуда будет составлять 1/3 начальной.
Затухают колебания также и потому, что часть энергии излучается.
Зависимость 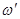 от
от 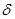
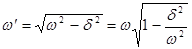 .
.
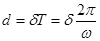 ,
, 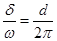 .
.
Если 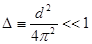 , то
, то 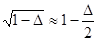 , т.е.
, т.е.
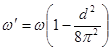 .
.
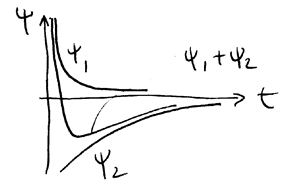
Пусть 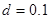 - довольно большое затухание! Даже в этом случае
- довольно большое затухание! Даже в этом случае 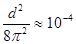 , т. е. различие между
, т. е. различие между 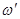 и
и 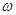 незначительно.
незначительно.
Если 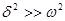 , то уравнение
, то уравнение 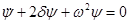 имеет решение вида
имеет решение вида
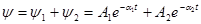 , где
, где 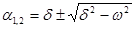 .
.
 |
В зависимости от соотношения между
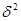 и
и 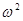 , а также от начальных условий (знаки
, а также от начальных условий (знаки 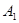 и
и 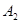 ) могут быть разные случаи, например:
) могут быть разные случаи, например: РИС.24-11
Поведение осциллятора под действием внешней силы, действующей периодически с частотой 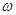 .
.
Имеется колебательная система, ее собственная частота 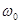 :
:
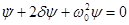 . Это однородное уравнение.
. Это однородное уравнение.
Теперь колебания не являются свободными, действует сила 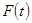 :
:
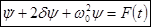 . Это неоднородное уравнение.
. Это неоднородное уравнение.
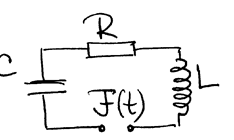 |
РИС.24-12
Одно из частных решений неоднородного уравнения:
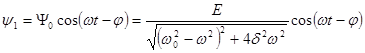 .
.
Чтобы получить общее решение неоднородного уравнения, надо добавить сюда общее решение однородного уравнения 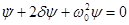 :
:
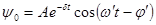 ,
, 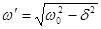 .
.
Получаем: 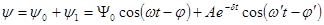 ,
,
где 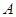 и
и 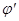 определяются из начальных условий задачи.
определяются из начальных условий задачи.
Из полученного общего решения видно, что через достаточно большой промежуток времени затухающие колебания сделаются сколь угодно малыми, и останется только периодическое движение.
Переходной процесс Þ затем установившийся процесс.
Вынужденное колебание происходит на частоте 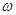 независимо от собственной частоты колебаний
независимо от собственной частоты колебаний 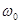 .
.
Резонанс
Резонансом называется процесс увеличения амплитуды вынужденных колебаний, развивающийся при приближении частоты вынуждающей силы 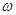 к собственной частоте системы
к собственной частоте системы 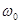 .
.
Фиксируем 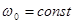 , меняем
, меняем 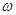 .
.
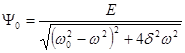 .
.
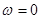 : постоянно приложена некая сила.
: постоянно приложена некая сила.
Начальное смещение системы: 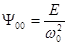 .
.
Начали изменять 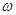 ; максимум будет достигнут при условии
; максимум будет достигнут при условии
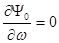 , т.е. при частоте
, т.е. при частоте 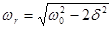 - резонансная частота,
- резонансная частота, 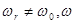 ;
; 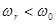 .
.
При этом максимальное значение амплитуды
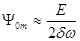 в отсутствие затухания амплитуда в максимуме бесконечна.
в отсутствие затухания амплитуда в максимуме бесконечна.
При увеличении затухания максимум уменьшается, а резонансная частота смещается в сторону более низких частот.
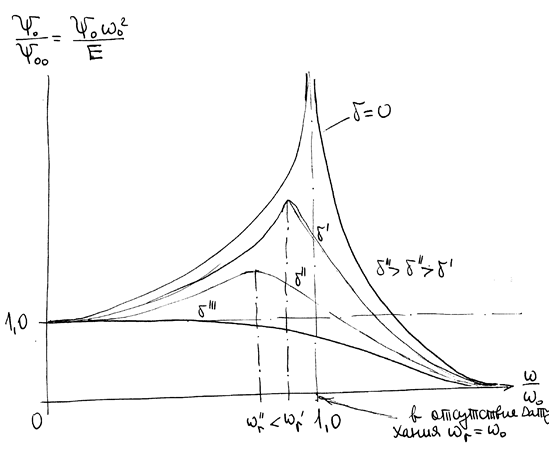
РИС.24-13
Ищем максимум амплитуды тока в контуре (т.е. скорости смещения) 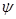 :
:
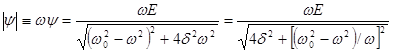 .
.
Резонанс тока (скорости смещения) наступает при условии 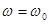 .
.
О сдвиге фаз 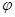 :
:
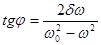 .
.
Если частота внешней силы мала (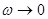 ), то сдвиг фаз между вынуждающей силой и смещением
), то сдвиг фаз между вынуждающей силой и смещением 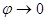 , колебания происходят в фазе.
, колебания происходят в фазе.
Если частота вынуждающей силы очень велика (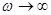 ), то
), то 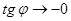 , т.е.
, т.е. 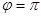 : смещение находится в противофазе с внешней силой.
: смещение находится в противофазе с внешней силой.
При резонансе, 
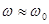 ,
, 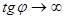 , сдвиг фаз
, сдвиг фаз 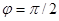 .
.
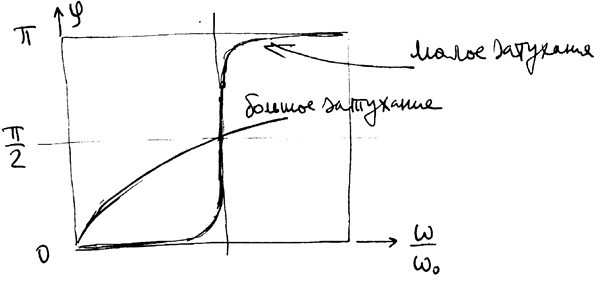 |
Чем меньше затухание, тем меньше нужно удалиться от резонанса для того, чтобы сдвиг фаз из
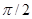 превратился в 0 или
превратился в 0 или 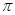 .
. РИС.24-14
Основные свойства вынужденных колебаний и резонанса
1) В установившемся режиме происходят незатухающие гармонические колебания с частотой действующей силы.
2) Амплитуда смещения максимальна, когда период возбуждающей силы приблизительно совпадает с периодом собственных колебаний системы.
3) Максимум выражен тем резче, чем меньше затухание.
4) Сдвиг фаз 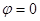 при
при 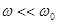 ,
, 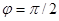 в резонансе,
в резонансе, 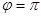 при
при 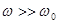 .
.
19 Лекция 19
20 Лекция 20
21 Лекция 21
22 Лекция 22
23 Лекция №23
24 Лекция №24
 2015-10-22
2015-10-22 2437
2437