Mathcad. Решение уравнений

1. Изучите работу с комплексными числами, выполнив следующие операции:

Z:= -3 + 2i |Z| = Re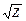(Z) = = = 2 × Z =

Z1:= 1 + 2i Z2:= 3 + Z1 + Z2 = Z1 - Z2 = Z1× Z2 =

2. Изучите метод решения одного уравнения с одним неизвестным и выполните примеры, приведенные в тексте учебного пособия на стр. 55.

Самостоятельно решите уравнения с одним неизвестным:

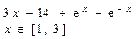
3. Изучите метод нахождения корней полинома n-й степени и выполните примеры, приведенные в тексте учебного пособия на стр. 56.

Самостоятельно найдите корни полиномов:

x⁴ - 2x³ + x² - 12x + 20 x⁴ - x³ + x² - 11x + 10 x⁴ - 7x³ + 7x² - 5x + 100

4. Изучите шаги алгоритма решения системы линейных уравнений на примере решения системы линейных уравнений x+2*y=3, 4*x+5*y=6:

ü Введите формулу, задающую матрицу коэффициентов системы линейных уравнений

ü Введите формулу, определяющую вектор свободных членов системы уравнений

ü Введите строку lsolve(A,B), где lsolve функция, которая находит решение системы линейных уравнений;

ü Второй способ решения: введите для матриц А и В формулу

ü Решите самостоятельно системы линейных уравнений двумя способами: в матричном виде и с помощью функции lsolve.

5. Изучите алгоритм поиска корней нелинейного уравнения f(x):=0.5*x+cos(x)-1, при x={0.1, 0.2,...5}

ü Введите функцию, определяющую значения x и функцию, определяющую уравнение f(x);

ü Постройте график функции f(x), для того, чтобы по графику определить приближенное значение x при f(x)=0;

ü С помощью функции root(f(x),x) определите значения функции f(x) в точках x:=4 и x:=0.

ü Решите самостоятельно нелинейные уравнения:

х ⁵ – х - 0,2, где х Î [1, 2]

6. Изучите метод решения систем нелинейных уравнений с помощью функций Find и Minnerr и выполните приведенные в тексте учебного пособия примеры стр. 56-58.

Решите самостоятельно системы нелинейных уравнений:

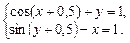
7. Изучите метод решения обыкновенных дифференциальных уравнений и выполните примеры, приведенные в тексте учебного пособия на стр. 58-59.

8. Познакомьтесь с элементами программирования в Mathcad, выполнив упражнения:

8.1 Использование линейных алгоритмов: Пусть необходимо вычислить значение выражения для произвольных значений x, y и z.

Процесс вычислений может быть выполнен следующими способами, показанными в таблице:

Самостоятельно вычислите значение выражения: , при A = 20, B = 2, C = 0.1 двумя способами;

8.2 Использование разветвляющихся алгоритмов:

ü Пусть необходимо вычислить значение следующей функции:

.

ü Вычисления f(x,y) выполнены с помощью оператора if и оператора otherwise панели Программирование, как показано на рисунке ниже.

ü Самостоятельно вычислите значения функции

Контрольные вопросы

1. Правила работы с комплексными числами в среде Mathcad.

2. Метод решения одного уравнения с одним неизвестным.

3. В чем заключается метод нахождения корней полинома n-й степени?

4. Назовите шаги алгоритма решения системы линейных уравнений.

5. Метод решения систем нелинейных уравнений с помощью функций Find и Minnerr.

6. Алгоритм поиска корней нелинейного уравнения.

7. Использование линейных алгоритмов в среде Mathcad.

8. Использование разветвляющихся алгоритмов в Mathcad.