Теорема. Если функция у = f(х) непрерывна на отрезке [а, b], а функция F(х) - любая ее первообразная (т.е. F`(х) = f(х)), то определенный интеграл от функции f(х) на [а, b] равен приращению первообразной F(х) на этом отрезке, т.е. 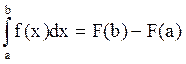 .
.
Данная формула является основной формулой интегрального исчисления, и ее доказательство основано на свойствах интеграла с переменным верхним пределом.
Докажем ее. В самом деле, поскольку производная от интеграла с переменным верхним пределом по верхнему пределу равна подынтегральной функции, можно сказать, что сам интеграл с переменным верхним пределом является первообразной для подынтегральной функции.
Так как первообразные одной и той же функции отличаются на постоянное слагаемое, можно утверждать, что найдется такое число С, что F(х) = Ф(х) + С. Тогда приращение первообразной имеет вид
F(b) – F(a) = (Ф(b) + С) - (Ф(a) + С) = Ф(b) - Ф(a) = 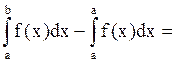
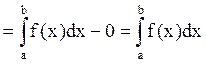
Теорема доказана.
Полученная формула сводит нахождение определенных интегралов к нахождению неопределенных интегралов. При этом приращение первообразной F(b) – F(a) принято обозначать 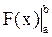 .
.
Подчеркнем, что при применении формулы Ньютона-Лейбница можно использовать любую первообразную для подынтегральной функции, например, имеющую наиболее простой вид при С = 0 (в дальнейшем не будем записывать константу при нахождении неопределенного интеграла, поскольку будем считать ее равной нулю).
Пример 1. Найти
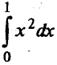
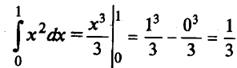
Пример 2. Найти
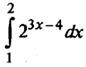
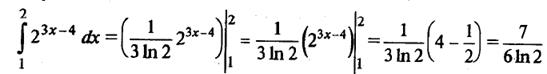
Отметим, что при нахождении приращения первообразной общий сомножитель был вынесен за скобки.
 2015-10-22
2015-10-22 941
941








