Если подынтегральная функция не представляет собой рациональную дробь, то во многих случаях можно рационализировать интеграл (свести искомый интеграл к интегралам от рациональных функций) с помощью замены переменной.
Обозначим через R(u, v) некоторую рациональную функцию от переменных u и v
Рассмотрим интегралы вида 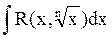 . Их можно рационализировать заменой переменной
. Их можно рационализировать заменой переменной 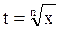 . Частными случаями данного случая являются интегралы вида
. Частными случаями данного случая являются интегралы вида 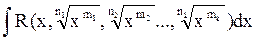 . Их также можно рационализировать такой же заменой переменной, где n – наименьшее общее кратное чисел n1, n2, …nk.
. Их также можно рационализировать такой же заменой переменной, где n – наименьшее общее кратное чисел n1, n2, …nk.
Для рационализации интегралов вида 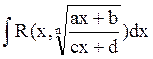 используют подстановку
используют подстановку 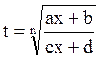 .
.
Если под знаком радикала стоит многочлен второй степени, т.е. интеграл имеет вид 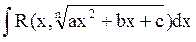 , то иногда интеграл можно свести к табличному, выделив в подкоренном выражении полный квадрат, не рационализируя интеграл. В более сложных случаях ипользуются подстановки Эйлера, которые здесь не рассматриваются. Иногда такие интегралы удается рационализировать, используя для замены переменной тригонометрические функции, как это рассмотрено в практикуме Кремера на стр. 278.
, то иногда интеграл можно свести к табличному, выделив в подкоренном выражении полный квадрат, не рационализируя интеграл. В более сложных случаях ипользуются подстановки Эйлера, которые здесь не рассматриваются. Иногда такие интегралы удается рационализировать, используя для замены переменной тригонометрические функции, как это рассмотрено в практикуме Кремера на стр. 278.
Интегралы вида 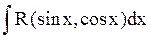 рационализируются с помощью тригономерических формул, выражающих синус и косинус через тангенс половинного аргумента и последующей замены переменной t = tg (x/2). Подробно этот метод рассмотрен в учебнике Кремера на стр.276.
рационализируются с помощью тригономерических формул, выражающих синус и косинус через тангенс половинного аргумента и последующей замены переменной t = tg (x/2). Подробно этот метод рассмотрен в учебнике Кремера на стр.276.
Пример 1. Найдем 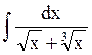 . В знаменателе подынтегральной функции стоят радикалы второй и третьей степеней. Наименьшим общим кратным для чисел 2 и 3 является число 6, поэтому осуществим замену переменной
. В знаменателе подынтегральной функции стоят радикалы второй и третьей степеней. Наименьшим общим кратным для чисел 2 и 3 является число 6, поэтому осуществим замену переменной 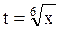 . Тогда t6 = x, dx = 6t5dt,
. Тогда t6 = x, dx = 6t5dt, 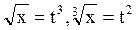 .
.
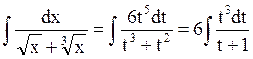 .
.
Еще раз осуществим замену переменной z = t + 1.
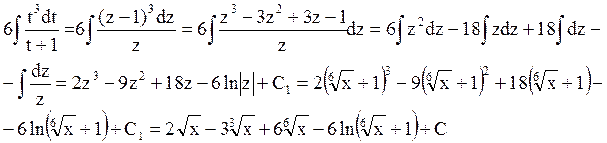
Пример 2. Найдем 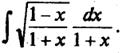
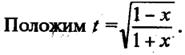 Тогда
Тогда
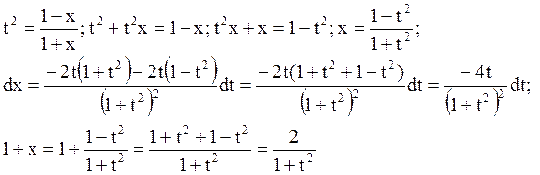
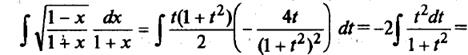
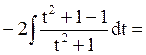
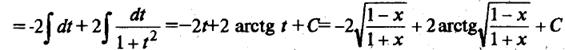
Из основных правил дифференцирования следует, что производная произвольной элементарной функции тоже является элементарной функцией. Операция нахождения неопределенного интеграла таким свойством не обладает, т.е. существуют элементарные функции, первообразные которых элементарными функциями уже не являются. Соответствующие неопределенные интегралы называются "неберущимися" в элементарных функциях, а сами функции - неинтегрируемыми в конечном виде. Например, функция 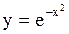 является неинтегрируемой в конечном виде, так как не существует такой элементарной функции, чтобы ее производная равнялась этой функции.
является неинтегрируемой в конечном виде, так как не существует такой элементарной функции, чтобы ее производная равнялась этой функции.
 2015-10-22
2015-10-22 4714
4714








