Физический смысл криволинейного интеграла II рода

Криволинейный интеграл II рода численно равен работе, которую совершает переменная сила на криволинейном пути MN.

Пример. Найти работу силы при перемещении по линии отточки к точке .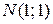

Решение.

3. Связь между двойными и криволинейными интегралами.

Формула Грина

Пусть L граница односвязной области D. и их частные производные непрерывны в замкнутой области D (включая ее границу L), то имеет место формула: .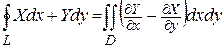

Пример. Вычислить криволинейный интеграл двумя способами: непосредственно и по формуле Грина. L – контур треугольника ABCA .

Решение. 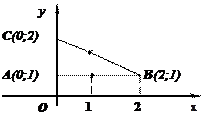1. Вычислим непосредственно криволинейный интеграл:

(BC) – прямая, проходящая через 2 точки, имеет уравнение:

.

.

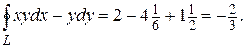
2. Вычисление интеграла по формуле Грина:

Итак, мы получили тот же результат: