2015-10-22
252
Криволинейный интеграл II рода по координате
Криволинейный интеграл II рода по координате записывается в виде
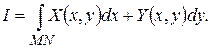
При условии, что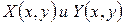 
непрерывны в точках дуги MN, а дуга – гладкая кривая 
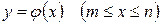, интеграл существует и вычисляется как определенный интеграл по формуле:
.
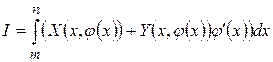Кроме обычных свойств интеграла отметим, что
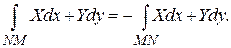
Если путь интегрирования простая замкнутая кривая L, то его обозначают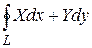 
, вычисляют в направлении против часовой стрелки и называют циркуляцией.
