КОНТРОЛЬНАЯ РАБОТА
Задание 1.
Дана система линейных уравнений:
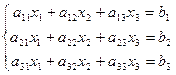
Решить систему методами Гаусса и Крамера.
| № вар. | Коэффициенты | Свободные члены | № вар. | Коэффициенты | Свободные члены |
| 1. | 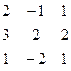
| 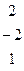
| 11. | 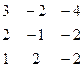
| 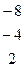
|
| 2. | 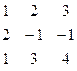
| 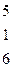
| 12. | 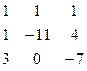
| 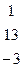
|
| 3. | 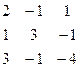
| 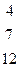
| 13. | 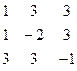
| 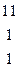
|
| 4. | 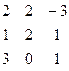
| 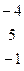
| 14. | 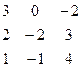
| 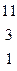
|
| 5. | 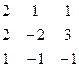
| 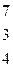
| 15. | 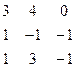
| 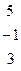
|
| 6. | 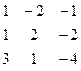
| 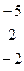
| 16. | 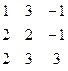
| 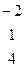
|
| 7. | 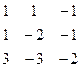
| 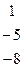
| 17. | 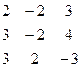
| 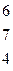
|
| 8. | 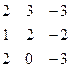
| 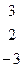
| 18. | 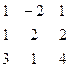
| 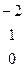
|
| 9. | 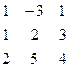
| 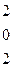
| 19. | 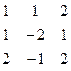
| 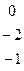
|
| 10. | 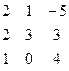
| 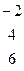
| 20. | 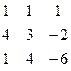
| 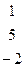
|
Задание 2.
Методом Гаусса найти общее решение системы и любых два базисных решения:
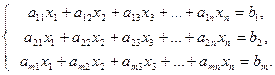
| № вар. | Коэффициенты | Свободные члены | № вар. | Коэффициенты | Свободные члены |
| 1. | 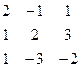
| 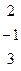
| 11. | 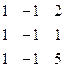 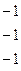
| 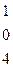
|
| 2. | 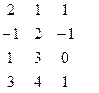
| 
| 12. | 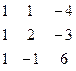 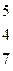
| 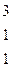
|
| 3. | 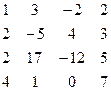
| 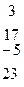
| 13. | 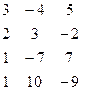
| 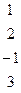
|
| 4. | 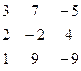 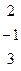 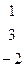
| 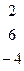
| 14. | 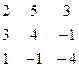 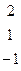
| 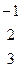
|
| 5. | 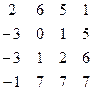
| 
| 15. | 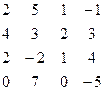
| 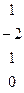
|
| 6. | 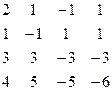 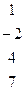
| 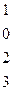
| 16. | 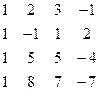
| 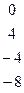
|
| 7. | 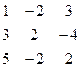
| 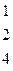
| 17. | 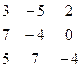 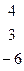
| 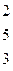
|
| 8. | 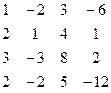
| 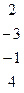
| 18. | 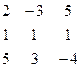
| 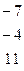
|
| 9. | 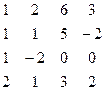
| 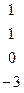
| 19. | 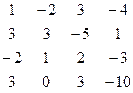
| 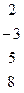
|
| 10. | 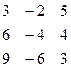 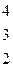
| 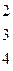
| 20. | 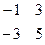 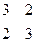 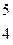
| 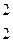
|
Задание 3.
Даны координаты вершин треугольника АВС. Найти:
1) длину стороны АВ;
2) уравнение сторон АВ и ВС и их угловые коэффициенты;
3) внутренний угол В;
4) уравнение медианы АЕ;
5) уравнение высоты CD;
6) построить треугольник АВС.
| № | Координаты вершин | № | Координаты вершин |
| 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. | А(1;1), В(2;5), С(6;2) А(-3;1), В(2;4), С(3;-1) А(-1;-1), В(2;5), С(4;-2) А(1;-2), В(6;2), С(-1;6) А(-2;4), В(4;5), С(4;-2) А(1;3), В(8;5), С(6;-2) А(-5;-1), В(-4;6), С(1;0) А(1;-3), В(3;4), С(7;-2) А(-4;-2), В(1;5), С(3;-2) А(1;1), В(2;4), С(3;-3) | 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. | А(-3;-1), В(3;2), С(4;-3) А(-1;-1), В(5;1), С(4;-3) А(0;1), В(2;4), С(3;-3) А(-3;2), В(-1;5), С(2;0) А(-2;2), В(4;-3), С(3;2) А(-2;2), В(5;1), С(-2;-2) А(-1;-3), В(4;3), С(5;-3) А(-1;-1), В(1;3), С(2;4) А(-2;-1), В(5;4), С(6;-3) А(-2;2), В(3;4), С(1;-2) |
Задание 4.
Вычислить пределы:
| № | а | б | в |
| 1. | 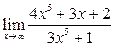
| 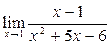
| 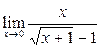
|
| 2. | 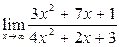
| 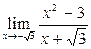
| 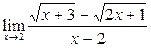
|
| 3. | 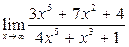
| 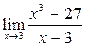
| 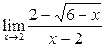
|
| 4. | 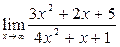
| 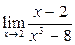
| 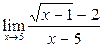
|
| 5. | 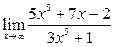
| 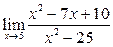
| 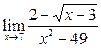
|
| 6. | 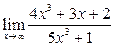
| 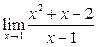
| 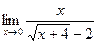
|
| 7. | 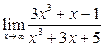
| 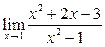
| 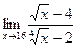
|
| 8. | 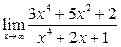
| 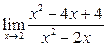
| 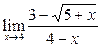
|
| 9. | 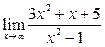
| 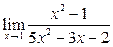
| 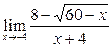
|
| 10. | 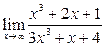
| 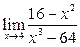
| 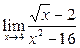
|
| 11. | 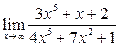
| 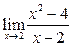
| 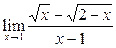
|
| 12. | 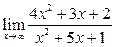
| 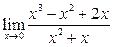
| 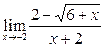
|
| 13. | 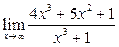
| 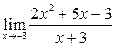
| 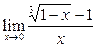
|
| 14. | 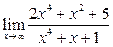
| 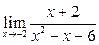
| 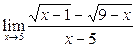
|
| 15. | 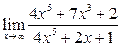
| 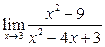
| 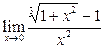
|
| 16. | 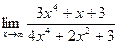
| 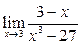
| 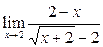
|
| 17. | 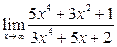
| 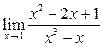
| 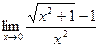
|
| 18. | 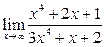
| 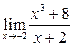
| 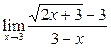
|
| 19. | 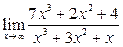
| 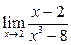
| 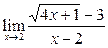
|
| 20. | 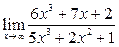
| 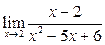
| 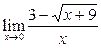
|
Задание 5.
Найти производные первого порядка данных функций:
| № | а | б | в |
| 1. | 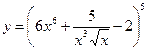
| 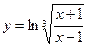
| 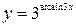
|
| 2. | 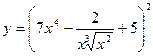
| 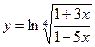
| 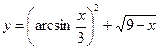
|
| 3. | 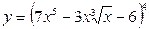
| 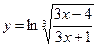
| 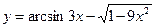
|
| 4. | 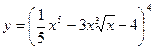
| 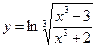
| 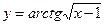
|
| 5. | 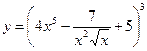
| 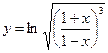
| 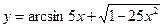
|
| 6. | 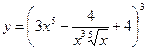
| 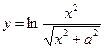
| 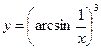
|
| 7. | 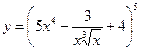
| 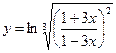
| 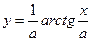
|
| 8. | 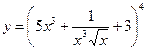
| 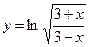
| 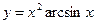
|
| 9. | 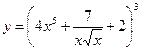
| 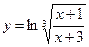
| 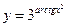
|
| 10. | 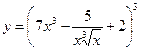
| 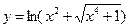
| 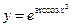
|
| 11. | 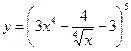
| 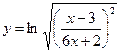
| 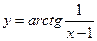
|
| 12. | 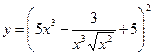
| 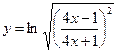
| 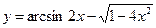
|
| 13. | 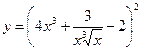
| 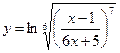
| 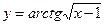
|
| 14. | 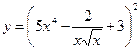
| 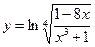
| 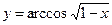
|
| 15. | 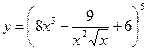
| 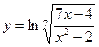
| 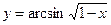
|
| 16. | 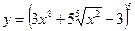
| 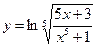
| 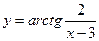
|
| 17. | 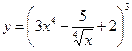
| 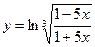
| 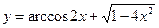
|
| 18. | 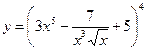
| 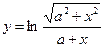
| 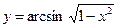
|
| 19. | 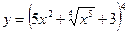
| 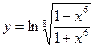
| 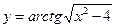
|
| 20. | 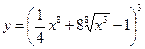
| 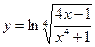
| 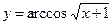
|
Задание 6.
Построить график функции, используя общую схему исследования функции:
| № | Функция | № | Функция |
| 1. | 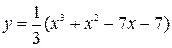
| 11. | 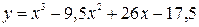
|
| 2. | 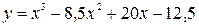
| 12. | 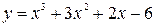
|
| 3. | 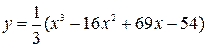
| 13. | 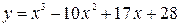
|
| 4. | 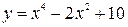
| 14. | 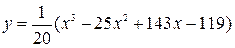
|
| 5. | 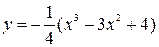
| 15. | 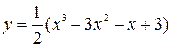
|
| 6. | 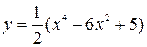
| 16. | 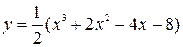
|
| 7. | 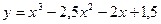
| 17. | 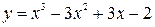
|
| 8. | 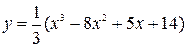
| 18. | 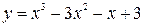
|
| 9. | 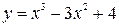
| 19. | 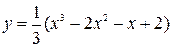
|
| 10. | 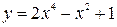
| 20. | 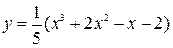
|
Задание 7.
Вычислить интегралы:
| а | б | |
| 1. | ∫(2 − 3 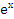 + х)dх + х)dх
| ∫ 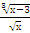 dх dх
|
| 2. | ∫(3 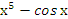 −1)dх −1)dх
| ∫ 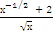 dх dх
|
| 3. | ∫(7 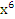 − − 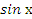 + 3)dх + 3)dх
| ∫ 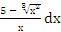
|
| 4. | ∫(7 − 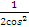 – – 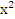 )dх )dх
| ∫ 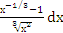
|
| 5. | ∫(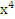 − − 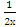 −4)dx −4)dx
| ∫ 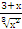 dх dх
|
| 6. | ∫(3 − 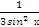 +2)dх +2)dх
| ∫ 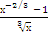 dх dх
|
| 7. | ∫(3 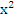 − − 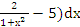
| ∫ 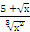 dх dх
|
| 8. | ∫(х − 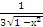 +2)dх +2)dх
| ∫ 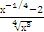 dх dх
|
| 9. | ∫(2 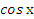 −5 −5 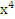 +3)dх +3)dх
| ∫ 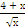 dх dх
|
| 10. | ∫(5 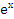 − − 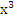 −4)dх −4)dх
| ∫ 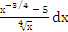
|
 2015-10-22
2015-10-22 236
236







