Виразіть шукану величину через ті, що стоять у дужках, а також фізичні та математичні константи

Наведена формула є виразом для роботи, яку виконує певна кількість ідеального газу при ізотермічному розширенні від об’єму до . Зрозуміло, що у відповідь буде входити універсальна газова стала , хоча в дужках вона відсутня.

Оскільки шукана величина зустрічається в формулі тільки один раз, треба послідовно її “витягувати” з того “оточення”, в якому вона знаходиться:

6. Розв’яжіть систему рівнянь і виразіть шукану величину через ті, що стоять у дужках, а також математичні та фізичні константи:

Одна з проблем, яка виникає під час виконання завдань такого типу, полягає у тому, що деякі абітурієнти не розуміють умови завдання і тому навіть не намагаються його виконувати або лише бездумно пишуть співвідношення між окремими величинами, що входять до системи. Тому спочатку пояснимо, як потрібно розуміти умову завдання.

У математиці словосполучення “ розв’язати систему рівнянь ” означає, що треба знайти такі числові значення невідомих величин, при підстановці яких до рівнянь системи останні перетворюються у тотожності.

У фізиці системи рівнянь виникають, в основному, під час розв’язування задач. Причому часто трапляється так, що неможливо відразу скласти рівняння, до якого б входили тільки величини, подані в умові задачі, та деякі сталі. Тоді доводиться вводити нові невідомі величини (вони не повинні входити до кінцевої відповіді, тому у процесі розв’язування системи рівнянь їх потрібно виключати). Ці величини виконують допоміжну функцію: дозволяють записати декілька співвідношень між величинами, що входять до умови, а також пов’язують шукану в задачі величину з даними в умові.

Отже, словосполучення “ виразіть шукану величину через ті, що стоять у дужках, а також математичні та фізичні константи ” означає, що невідому величину потрібно подати у вигляді комбінації величин, що стоять у дужках (вони вважаються відомими), а також математичних та фізичних констант (якщо є така необхідність). Інші величини не повинні входити до отриманого виразу.

Ми визначили, що у фізиці фраза “ розв’язати систему рівнянь ” означає виразити шукану величину через ті, що вважаються відомими.

Тепер перейдемо до розв’язку конкретної системи рівнянь. Ми вже визначили, що величину , яка є невідомою, необхідно подати у вигляді комбінації величин та (у цій системі рівнянь фізичні сталі відсутні). Величини та є допоміжними, тому їх треба послідовно виключати з рівнянь системи.

У другому рівнянні бачимо комбінацію допоміжних величин , яку можна виразити з першого рівняння через відомі величини:

.

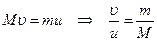Тоді отримаємо систему, що складається з двох рівнянь:

Тепер з першого рівняння отриманої системи можна виразити допоміжну величину, що залишилася: . Маємо рівняння , звідки знайдемо шукану величину:

.

7. Виберіть до виразу одну з наступних одиниць: м, кг, с, Ом, А, Н, Дж, Па, Гн, Ф, Тл, Вб, Кл, К, В, Вт, Гц.

Примітка: — заряд електрона, — швидкість світла в вакуумі, — стала Планка, — гравітаційна стала, — електрична стала.

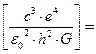
Квадратні дужки означають, що ми маємо справу тільки з одиницями вимірювання фізичних констант, а числові значення не враховуватимуться. Якщо знати, в яких одиницях вимірюється кожна константа, можна спробувати “розписати” їхню комбінацію через основні одиниці СІ. Потім замінити отриману відповідь тільки однією одиницею з наведеного списку. Але цей шлях нераціональний, хоча формально правильний.

Можна спробувати “пробитися” іншим, коротшим шляхом, використовуючи знання фізичних формул. Звернемо увагу на той факт, що всі константи у примітці входять до різноманітних формул для розрахунку енергії: (спокою електрона), (фотона), (гравітаційної взаємодії двох матеріальних точок), (взаємодії двох нерухомих точкових зарядів). Зрозуміло, що , а . Тому ми можемо записати:

.

Тож у завданні треба умовно виділити або сформувати “блоки”, що за одиницями вимірювання відповідають енергії, і в які входять використані константи. Якщо пощастить знайти такі комбінації і в чисельнику, і в знаменнику, то їх можна буде скоротити, тим самим спростивши вираз. Якщо для утворення якоїсь комбінації знадобиться певна величина, то її можна дописати одночасно в знаменник та чисельник.

Останнє, що може стати у пригоді у конкретній розглядуваній вправі, так це формула зв’язку довжини хвилі та частоти: . Одиниці довжини хвилі такі самі, як і одиниці відстані, отже, маємо: .

Подивіться уважно на запропоновану комбінацію .У чисельнику при наявності ще одного та 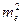утворюється квадрат енергії (), а також якщо в знаменнику стояв би — ще один квадрат енергії (). Тому ми можемо записати наступний крок, помноживши чисельник та знаменник на необхідні , 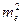та : , де — енергія. Тепер у знаменнику можна утворити комбінацію, що дає розмірність енергії (), яку потім можна скоротити з енергією у чисельнику. Залишається вираз . Пригадаємо, що . Тому . Помноживши останній вираз на скорочуємо на , бо . Залишається . Цей вираз має одиницю вимірювання Дж/с, тобто Вт. Ця одиниця входить до переліку одиниць у примітці. Остаточно маємо: .

Треба намагатися якомога більше операцій прокручувати в думці і не розписувати все так докладно. Ми це робили, щоб розкрити ідею розв’язку.

8. Виберіть до виразу одну з наступних одиниць: м, кг, с, Ом, А, Н, Дж, Па, Гн, Ф, Тл, Вб, Кл, К, В, Вт, Гц.

Примітка: — гравітаційна стала, — довжина, — сила.

Як бачимо, в умові завдання крім фізичних сталих використовуються фізичні величини (у нашому випадку — довжина та сила), що відрізняє його від попереднього. Для успішного виконання цього завдання необхідне знання формул, до яких входять подані в умові фізичні величини та сталі, і вміння виконувати найпростіші математичні операції.

У нашому прикладі величини і входять до формули, яка виражає закон всесвітнього тяжіння (), де та — маси взаємодіючих точкових тіл, — відстань між ними. Тоді можна записати, що . Користуючись отриманим результатом, перетворимо поданий в умові вираз: . Оскільки , маємо 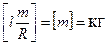. Отже, отримали, що .

9. Виберіть до виразу одну з наступних одиниць: м, кг, с, Ом, А, Гц, Н, Дж, Па, Гн, Ф, Тл, Вб, Кл, К, В, Вт.

Ідею розв’язку такого типу завдань докладно описано в завданні номер 8 з першого параграфу. Тут зупинимося лише на розв’язанні окремого прикладу, тому що для засвоєння операцій необхідне їх неодноразове відпрацьовування.

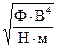Для зручності внесемо під знак радикалу множник . Тоді отримаємо . Потім, користуючись фізичними формулами, знайдемо в чисельнику і знаменнику комбінації одиниць вимірювання, які можна замінити однією і тією ж одиницею:

,

.

Після скорочення отримаємо .

10. Матеріальна точка рухається так, що координата змінюється за законом: . Запишіть вираз для дотичної до графіка цієї залежності в початковий момент у вигляді . Який фізичний зміст мають константи А і В?

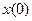Останнє запитання допомагає виконати вправу. Дійсно, порівняємо вираз з таким: . З цього порівняння видно, що — початкова координата , а — початкова проекція швидкості на вісь . Щоб знайти , треба тільки підставити у вираз для : (м).

А для того, щоб знайти , необхідно спочатку знайти похідну за часом від : (точка над означає похідну за часом!). Після цього підставляємо :

(м/с).

Таким чином, дотичною буде пряма .

Корисно знати, що функція , яка має похідну будь-якого порядку при , може бути наближена поліномом Заміну таким поліномом називають розкладанням у ряд Маклорена. Порівнюючи значення вихідної функції і полінома при , отримуємо . Порівнюючи значення перших похідних при , знайдемо, що . Продовжуючи цю процедуру, маємо ,

Оскільки будь-яка похідна від 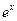дорівнює 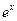, а , то Зрозуміло, що для нашої вправи достатньо обмежитися першими двома членами ряду: . Тоді .

Легко отримати розклад у ряд Маклорена і для інших функцій. Зокрема,

;

Але, якщо нам треба знайти дотичну до графіка в точці з абсцисою , то нам достатньо скористатися такими наближеннями: ; .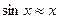

Наприклад, знайти дотичну до графіка функції у точці з за допомогою ряду Маклорена дуже просто: . Як бачимо, такі вправи можна виконувати усно.

11.Не розв’язуючи повністю задачу, вкажіть відповідь у тому конкретному випадку, який запропонований у дужках після умови.

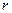Паралельно з’єднані конденсатор ємністю і резистор опором під’єднані до джерела струму з ЕРС і внутрішнім опором . Визначити заряд на обкладках конденсатора. ()

Одним з обов’язкових етапів розв’язування фізичних задач є оцінка вірогідності отриманої відповіді. Але в реальній шкільній практиці про нього часто забувають, бо в більшості випадків є можливість звіритися з відповіддю, яку можна знайти в підручнику чи задачнику.

Майже всіх абітурієнтів учили в школі перевіряти кінцеву формулу на розмірність, а ось перевіряти на окремі та граничні випадки вчили далеко не всіх. Щоб виконати таку перевірку, треба спочатку себе запитати: “Що чекати від відповіді задачі?”. У завданні запропонованого типу розглядається лише один аспект цього питання: “Яку відповідь буде мати спрощена задача?”. Звернемось до наведеної умови конкретної фізичної задачі.

У спрощеному варіанті пропонується розглянути випадок: . Така умова означає, що джерело струму буде фактично накоротко замкненим. При цьому ЕРС джерела струму буде дорівнювати падінню напруги на внутрішньому опорі, а напруга на резисторі буде дорівнювати нулю. Таким чином, конденсатор виявляється фактично не зарядженим. Іншими словами, правильна відповідь для заряду конденсатора у вихідній задачі повинна прямувати до нуля за умови . Ось і вся вправа! Вона, як бачите, виконується усно.

Припустимо, що хтось розв’язав вихідну задачу і отримав таку відповідь: . Вона витримує перевірку на розмірність, але . Тому цю відповідь треба визнати невірною, бо вона не пройшла перевірку на граничний випадок. Правильна відповідь вихідної задачі така: . Легко бачити, що , як і повинно бути.

Треба зазначити, що перевірка на граничні та окремі випадки не гарантує правильності знайденої кінцевої формули, але вона допомагає в багатьох випадках помітити її помилковість.

Розглянемо тут ще один варіант цієї ж вправи. Вихідною задачею буде та сама, але пропонується отримати відповідь для випадку .

Якщо 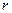набагато менше за (), а це те саме, що , то падіння напруги на внутрішньому опорі буде значно менше за напругу на резисторі та, відповідно, на конденсаторі. Таким чином, на конденсаторі буде напруга, що дорівнює ЕРС джерела струму, а значить,

Легко встановити, що відповідь вихідної задачі, яку ми навели як правильну, витримує перевірку і на цей граничний випадок: .

Розгляд граничних і окремих випадків не завжди буває простим, але в білетах для вступників на фізичний факультет ЗДУ не було складних завдань цього типу. Не дивлячись на це, абітурієнти погано впоралися з такими усними вправами.

У декого були проблеми навіть із наступним завданням: “ Стержень довжиною і масою підвішений до стелі на двох легких проводах однакової довжини. Проводи закріплені на кінцях стержня і паралельні один до одного. Система розміщена в однорідному вертикальному магнітному полі з індукцією . Чому дорівнюватиме натяг кожного проводу, якщо по стержню пропустити струм силою ? Не розв’язуючи повністю задачу, вкажіть відповідь у випадку ”.

Для абітурієнта фізичного факультету повинно бути очевидним, що за умови магнітне поле не буде діяти на стержень. Відповідно, сила тяжіння буде компенсуватися силами натягу проводів. Отже, натяг кожного з них дорівнюватиме .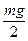

Радимо не тільки переглянути всі завдання цього типу, які розміщені у додатках до нашого посібника, а і потренуватися у прогнозуванні властивостей відповідей інших фізичних задач. А після отримання кінцевої відповіді в кожній задачі перевірте, чи має вона прогнозовані властивості, зокрема, чи витримує перевірку на граничні та окремі випадки.