Наведемо приклади завдань, що використовувалися на олімпіадах для абітурієнтів фізичного факультету Запорізького державного університету.
1. Розв’яжіть систему рівнянь і виразіть шукану величину через ті, що стоять у дужках:
а) 
Таку систему потрібно навчитися розв’язувати усно, без олівця та паперу. Вона дає можливість відновити в пам’яті вираз для моменту інерції  суцільної кулі, маса якої
суцільної кулі, маса якої  , а радіус
, а радіус  . Момент інерції тіла — важливе поняття динаміки обертального руху. Наприклад, кінетична енергія тіла, яке обертається навколо осі з кутовою швидкістю
. Момент інерції тіла — важливе поняття динаміки обертального руху. Наприклад, кінетична енергія тіла, яке обертається навколо осі з кутовою швидкістю 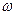 , обчислюється за формулою
, обчислюється за формулою  . Зміст перших двох рівнянь очевидний, а останні два можуть вимагати деяких пояснень. Третє рівняння дає можливість обчислити момент інерції суцільної кулі відносно її центру:
. Зміст перших двох рівнянь очевидний, а останні два можуть вимагати деяких пояснень. Третє рівняння дає можливість обчислити момент інерції суцільної кулі відносно її центру:  , де
, де 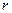 — відстань від центру кулі до диференціально малої її частинки масою
— відстань від центру кулі до диференціально малої її частинки масою  , а інтегрування ведеться за всім об’ємом кулі. Сам момент інерції відносно точки не має фізичного змісту. До фізичних формул входить момент інерції тіла відносно осі. Він визначається як
, а інтегрування ведеться за всім об’ємом кулі. Сам момент інерції відносно точки не має фізичного змісту. До фізичних формул входить момент інерції тіла відносно осі. Він визначається як  , але під
, але під 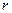 тут розуміють відстань до осі, а не до точки. Легко довести теорему, що
тут розуміють відстань до осі, а не до точки. Легко довести теорему, що  , де
, де  ,
,  ,
,  — моменти інерції тіла відносно трьох взаємно перпендикулярних осей, котрі проходять через точку, відносно якої момент інерції дорівнює
— моменти інерції тіла відносно трьох взаємно перпендикулярних осей, котрі проходять через точку, відносно якої момент інерції дорівнює  . У нашому випадку
. У нашому випадку 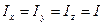 , де
, де  — момент інерції відносно будь-якої осі, яка проходить через центр кулі. Звідси і взялося четверте рівняння в розглядуваній системі. Теорема, про яку ми згадали, допомагає у багатьох випадках скоротити обчислення.
— момент інерції відносно будь-якої осі, яка проходить через центр кулі. Звідси і взялося четверте рівняння в розглядуваній системі. Теорема, про яку ми згадали, допомагає у багатьох випадках скоротити обчислення.
Формально для розв’язування запропонованої системи не потрібно знати, звідки взялися рівняння, але ці знання надають осмисленості діяльності з виконання завдання. Крім того, може виникнути бажання самостійно довести згадану нами теорему, або зрозуміти, як інтеграл  у конкретному випадку перетворився в той, що записаний у третьому рівнянні системи. Сам же процес розв’язування системи дуже простий. Обчислення інтегралу з третього рівняння дає
у конкретному випадку перетворився в той, що записаний у третьому рівнянні системи. Сам же процес розв’язування системи дуже простий. Обчислення інтегралу з третього рівняння дає 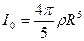 , а після замін з використанням перших двох рівнянь
, а після замін з використанням перших двох рівнянь  . З урахуванням четвертого рівняння системи остаточно отримуємо вираз для моменту інерції суцільної кулі відносно осі, яка проходить через її центр:
. З урахуванням четвертого рівняння системи остаточно отримуємо вираз для моменту інерції суцільної кулі відносно осі, яка проходить через її центр:  .
.
б) 
Якщо звернути увагу на те, що  , то відповідь можна записати відразу:
, то відповідь можна записати відразу:  . На жаль, як показує досвід, далеко не всі абітурієнти звертають увагу на подібні речі. У результаті — вправа залишається не виконаною, або відповідь наводиться у вигляді:
. На жаль, як показує досвід, далеко не всі абітурієнти звертають увагу на подібні речі. У результаті — вправа залишається не виконаною, або відповідь наводиться у вигляді:  . Хоча формально така відповідь правильна, але вона свідчить не на користь абітурієнта.
. Хоча формально така відповідь правильна, але вона свідчить не на користь абітурієнта.
в) 
Легко отримати залежність сили від часу  . Для цього треба знайти другу похідну від
. Для цього треба знайти другу похідну від  за часом, а потім помножити її на
за часом, а потім помножити її на  :
:
 ;
;
 ;
;
 .
.
А ось отримання виразу для сили через швидкість  викликає у помітної частини абітурієнтів не дуже зрозумілі труднощі. Хоча залишається тільки замінити
викликає у помітної частини абітурієнтів не дуже зрозумілі труднощі. Хоча залишається тільки замінити  на
на  . Отже,
. Отже, 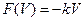 .
.
г) 
Це система рівнянь для знаходження сили натягу 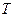 нитки довжиною
нитки довжиною  , на якій висить маленьке тіло масою
, на якій висить маленьке тіло масою  , після надання цьому тілу горизонтальної швидкості. Вважається відомим, що максимальний кут відхилення нитки від вертикального положення становив
, після надання цьому тілу горизонтальної швидкості. Вважається відомим, що максимальний кут відхилення нитки від вертикального положення становив  . Перше рівняння відбиває закон збереження механічної енергії: початкова кінетична енергія тіла
. Перше рівняння відбиває закон збереження механічної енергії: початкова кінетична енергія тіла  повністю переходить в потенціальну енергію
повністю переходить в потенціальну енергію  при максимальному куті відхилення нитки. Друге рівняння показує, як геометрично пов’язана висота підйому тіла
при максимальному куті відхилення нитки. Друге рівняння показує, як геометрично пов’язана висота підйому тіла  з кутом відхилення нитки
з кутом відхилення нитки  через її довжину
через її довжину  . Останнє рівняння — запис другого закону Ньютона для початкового моменту, коли нитка вертикальна, а швидкість тіла
. Останнє рівняння — запис другого закону Ньютона для початкового моменту, коли нитка вертикальна, а швидкість тіла  спрямована горизонтально. Доцентрове прискорення
спрямована горизонтально. Доцентрове прискорення  і сила натягу
і сила натягу 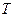 спрямовані вгору, а сила тяжіння
спрямовані вгору, а сила тяжіння  — вниз. Підстановка
— вниз. Підстановка  з другого рівняння в перше дає змогу отримати вираз для
з другого рівняння в перше дає змогу отримати вираз для  , який і треба підставити в останнє рівняння системи. Звідки остаточно маємо:
, який і треба підставити в останнє рівняння системи. Звідки остаточно маємо:  .
.
д) 
Це дуже проста вправа. Але бувають випадки, коли і з нею не можуть упоратися абітурієнти.
Перше рівняння в системі — це так зване основне рівняння молекулярно-кінетичної теорії, яке дозволяє виразити макропараметр  (тиск ідеального газу) через мікропараметри: концентрацію молекул
(тиск ідеального газу) через мікропараметри: концентрацію молекул  , масу однієї молекули
, масу однієї молекули 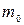 та середньоквадратичну швидкість молекул
та середньоквадратичну швидкість молекул  . А друге рівняння в системі — це вираз для
. А друге рівняння в системі — це вираз для  через абсолютну (термодинамічну) температуру
через абсолютну (термодинамічну) температуру 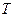 і масу молекули. Буквою
і масу молекули. Буквою  позначена стала Больцмана. Використовуючи вираз для
позначена стала Больцмана. Використовуючи вираз для  з другого рівняння, отримаємо
з другого рівняння, отримаємо  , звідки
, звідки  .
.
2. Координата матеріальної точки масою  змінюється за законом:
змінюється за законом:
 .
.
а) Як залежить від часу швидкість  матеріальної точки?
матеріальної точки?
б) Як залежить від часу прискорення  матеріальної точки?
матеріальної точки?
в) Як залежить від координати сила  , що діє на матеріальну точку?
, що діє на матеріальну точку?
г) Яка початкова координата матеріальної точки  ?
?
д) Яка початкова швидкість матеріальної точки  ?
?
а)  .
.
Іноді абітурієнти запитують: “Тут косинус добутку  і
і 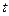 , чи добуток
, чи добуток 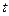 і косинуса
і косинуса  ?” Таке питання свідчить про те, що його автори не розуміють фізичного змісту формули і намагаються формально виконати вправу. Зрозумівши, що
?” Таке питання свідчить про те, що його автори не розуміють фізичного змісту формули і намагаються формально виконати вправу. Зрозумівши, що  — коефіцієнт жорсткості пружини,
— коефіцієнт жорсткості пружини,  — маса тягарця, а
— маса тягарця, а 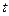 — час, вже легко встановити (навіть, якщо не пам’ятати, що
— час, вже легко встановити (навіть, якщо не пам’ятати, що  — циклічна частота коливань пружинного маятника), що
— циклічна частота коливань пружинного маятника), що  — розмірна величина. А ось
— розмірна величина. А ось  — безрозмірна. Для косинуса аргументом може бути тільки величина, яка не має розмірності.
— безрозмірна. Для косинуса аргументом може бути тільки величина, яка не має розмірності.
б) 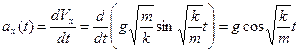 .
.
в)  .
.
Але нам потрібно з’ясувати, як  залежить від
залежить від  . Для цього з вихідного виразу для
. Для цього з вихідного виразу для  знайдемо, що
знайдемо, що  . Таким чином,
. Таким чином,  .
.
г) Початкова координата  .
.
д) Початкова швидкість  .
.
На запитання цієї вправи можна було відповісти дуже швидко, збагнувши, що вихідна формула описує коливання тягарця на пружині у полі тяжіння, причому в початковий момент пружина була не розтягнутою, а тягарець нерухомим.
3. При яких значеннях аргументу функція набуває максимальної величини? (Вважайте параметри  додатними).
додатними).
а)  ,
,  ;
;
б)  ,
,  ;
;
в)  ,
,  ;
;
г)  ,
,  ;
;
д)  ,
,  .
.
а) Скориставшись формулою з тригонометрії 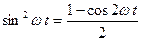 , отримуємо
, отримуємо  . Тепер легко уявити собі графік функції (див. рис. 11).
. Тепер легко уявити собі графік функції (див. рис. 11).
 З урахуванням вимоги
З урахуванням вимоги  для значень
для значень 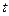 , при яких функція набуває максимальної величини, отримуємо:
, при яких функція набуває максимальної величини, отримуємо:  ,
,  Можна записати і так:
Можна записати і так:  ,
,  .
.
Зрозуміло, що досліджувана функція давала залежність від часу потужності джоулева тепла, що виділяється на резисторі з опором 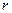 при проходженні змінного струму, якщо
при проходженні змінного струму, якщо  .
.
 б) Ця формула (
б) Ця формула ( ,
,  )показує, як змінюється заряд на конденсаторі ємності
)показує, як змінюється заряд на конденсаторі ємності  при його розрядженні через резистор з опором
при його розрядженні через резистор з опором  . Тому максимальне значення буде при
. Тому максимальне значення буде при  . Якщо навіть не знати фізичного змісту цієї формули, то легко уявити собі графік функції
. Якщо навіть не знати фізичного змісту цієї формули, то легко уявити собі графік функції  (див. рис. 12).
(див. рис. 12).
в) З урахуванням того, що  , можна уявити собі графік функції
, можна уявити собі графік функції  ,
,  (див. рис. 13).
(див. рис. 13).
Оскільки  , відповідь може бути записана так:
, відповідь може бути записана так:  ,
,  .
.
г) Ця формула ( ,
,  )описує траєкторію тіла, кинутого з початковою швидкістю
)описує траєкторію тіла, кинутого з початковою швидкістю  під кутом
під кутом 
 до горизонту з точки з координатами
до горизонту з точки з координатами  . Її легко отримати з очевидної системи рівнянь:
. Її легко отримати з очевидної системи рівнянь: 
Графік  — це квадратична парабола, гілки якої спрямовані вниз (рис. 14).
— це квадратична парабола, гілки якої спрямовані вниз (рис. 14).
Можна знайти шукане значення  , при якому
, при якому  набуває максимальної величини, прирівнюючи до нуля похідну
набуває максимальної величини, прирівнюючи до нуля похідну  :
:  . Тут ми скористалися тригонометричною формулою
. Тут ми скористалися тригонометричною формулою  . Можна було знайти “дальність польоту”
. Можна було знайти “дальність польоту”  , прирівнюючи до нуля
, прирівнюючи до нуля  і відкидаючи корінь
і відкидаючи корінь  . А потім, скориставшись симетрією квадратичної параболи, остаточно отримати
. А потім, скориставшись симетрією квадратичної параболи, остаточно отримати  .
.
 Наведемо ще один варіант виконання вправи (фізичний!). Час підйому тіла визначається як час, за який вертикальна складова швидкості зменшиться від
Наведемо ще один варіант виконання вправи (фізичний!). Час підйому тіла визначається як час, за який вертикальна складова швидкості зменшиться від  до нуля. Зрозуміло, що такий час дорівнює
до нуля. Зрозуміло, що такий час дорівнює 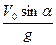 . У горизонтальному напрямку тіло рухається зі сталою швидкістю
. У горизонтальному напрямку тіло рухається зі сталою швидкістю  . Отже,
. Отже,  .
.
д) Ця формула ( ,
,  ) дає залежність потужності джоулева тепла, що виділяється на резисторі, від його опору
) дає залежність потужності джоулева тепла, що виділяється на резисторі, від його опору  . Джерело електричного струму характеризується значенням електрорушійної сили
. Джерело електричного струму характеризується значенням електрорушійної сили  і внутрішнім опором
і внутрішнім опором 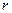 . Якщо
. Якщо  , то
, то 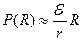 . Тобто при малих значеннях
. Тобто при малих значеннях  потужність зростає майже пропорційно
потужність зростає майже пропорційно  . При
. При  апроксимуючою (наближеною) функцією є
апроксимуючою (наближеною) функцією є  , тобто потужність спадає обернено пропорційно
, тобто потужність спадає обернено пропорційно  при великих значеннях
при великих значеннях  . Таким чином, можна очікувати максимум функції
. Таким чином, можна очікувати максимум функції 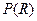 при деякому додатному значенні
при деякому додатному значенні  . Графік досліджуваної функції повинен мати вигляд такий, як на рис. 15.
. Графік досліджуваної функції повинен мати вигляд такий, як на рис. 15.
 Звичайно, можна знайти
Звичайно, можна знайти 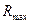 , при якому
, при якому 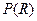 набуває максимального значення, прирівнявши до нуля похідну
набуває максимального значення, прирівнявши до нуля похідну  . Але можна піти іншим шляхом. Зрозуміло, що
. Але можна піти іншим шляхом. Зрозуміло, що 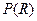 має максимум при тому самому значенні
має максимум при тому самому значенні  , при якому має мінімум функція
, при якому має мінімум функція 
 . А вона, у свою чергу, має мінімум при тому самому
. А вона, у свою чергу, має мінімум при тому самому  , що і функція
, що і функція  . Тут треба згадати знайому з уроків математики нерівність, яка виконується для додатних значень
. Тут треба згадати знайому з уроків математики нерівність, яка виконується для додатних значень  :
:  , причому рівність досягається при
, причому рівність досягається при 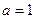 . Ця нерівність легко доводиться, виходячи з нерівності
. Ця нерівність легко доводиться, виходячи з нерівності  . У застосуванні до нашого випадку маємо
. У застосуванні до нашого випадку маємо 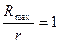 , тобто
, тобто 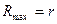 . Максимальна потужність джоулева тепла буде виділятися на резисторі, якщо його опір буде дорівнювати внутрішньому опору джерела струму.
. Максимальна потужність джоулева тепла буде виділятися на резисторі, якщо його опір буде дорівнювати внутрішньому опору джерела струму.
Існує інший шлях знайдення 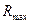 , що не використовує поняття похідної. Для цього спочатку треба знайти силу струму, при якій потужність джоулева тепла, що виділяється у резисторі, буде максимальною. Зрозуміло, що сила струму за законом Ома:
, що не використовує поняття похідної. Для цього спочатку треба знайти силу струму, при якій потужність джоулева тепла, що виділяється у резисторі, буде максимальною. Зрозуміло, що сила струму за законом Ома:  . Переходячи до нової змінної (
. Переходячи до нової змінної ( замість
замість  ), отримуємо:
), отримуємо:  Легко бачити, що
Легко бачити, що  – квадратична функція, нулі якої
– квадратична функція, нулі якої  і
і  , а графік – квадратична парабола, гілки якої спрямовані вниз. Максимум буде досягатися при
, а графік – квадратична парабола, гілки якої спрямовані вниз. Максимум буде досягатися при  . А для того, щоб сила струму мала таке значення, опір резистора повинен дорівнювати внутрішньому опору джерела струму.
. А для того, щоб сила струму мала таке значення, опір резистора повинен дорівнювати внутрішньому опору джерела струму.
5. Ідеальний газ розширюється від об’єму  до
до  так, що тиск змінюється за законом
так, що тиск змінюється за законом  . Знайдіть:
. Знайдіть:
1) Значення величини 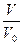 , при якому температура максимальна; 2) значення
, при якому температура максимальна; 2) значення  ; 3) роботу, що виконав газ у відносних одиницях (
; 3) роботу, що виконав газ у відносних одиницях ( ).
).
Побудуйте графіки процесу у координатах:
4) 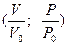 ; 5)
; 5)  .
.
Коментар. 1) За умовою газ є ідеальним, тоді для нього виконується закон Клапейрона-Менделєєва:  . Враховуючи даний в умові закон зміни тиску
. Враховуючи даний в умові закон зміни тиску  , отримаємо, що
, отримаємо, що  . Звідси маємо залежність
. Звідси маємо залежність  , яка є квадратичною функцією. Одним із способів знаходження максимуму даної функції є прирівнювання похідної до нуля. Маємо:
, яка є квадратичною функцією. Одним із способів знаходження максимуму даної функції є прирівнювання похідної до нуля. Маємо: 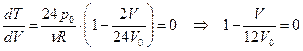 . Отже, максимальне значення температура набуває, коли
. Отже, максимальне значення температура набуває, коли  , або
, або  .
.
А можна скористатися тим, що нулі отриманої квадратичної функції –  і
і  . Відповідно, максимальне значення функція набуватиме при
. Відповідно, максимальне значення функція набуватиме при  , тобто
, тобто 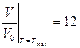 .
.
2) Використовуючи результат, отриманий у попередньому пункті, отримаємо значення  :
:
 .
.
Тоді шукана величина  .
.
3) Робота, яку виконав газ в описаному процесі, визначається формулою  . Розкриваючи дужки і розбиваючи отриманий інтеграл на два, отримаємо:
. Розкриваючи дужки і розбиваючи отриманий інтеграл на два, отримаємо:  . Перший інтеграл обчислюється дуже просто:
. Перший інтеграл обчислюється дуже просто: 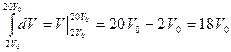 . Другий інтеграл теж відноситься до розряду табличних:
. Другий інтеграл теж відноситься до розряду табличних:  . Підставляючи отримані значення у вихідну формулу, отримаємо наступний результат:
. Підставляючи отримані значення у вихідну формулу, отримаємо наступний результат:  . Тоді робота, що виконав газ (у відносних одиницях), дорівнює
. Тоді робота, що виконав газ (у відносних одиницях), дорівнює  .
.
Враховуючи, що  – лінійна функція, можна було обійтися без інтегралів. За геометричним змістом робота
– лінійна функція, можна було обійтися без інтегралів. За геометричним змістом робота  – площа під графіком
– площа під графіком  , тобто площа трапеції з висотою
, тобто площа трапеції з висотою  і середньою лінією:
і середньою лінією:
 .
.
Отже, 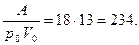
 4) Залежність
4) Залежність  є лінійною, отже графіком залежності
є лінійною, отже графіком залежності  буде пряма, рівняння якої
буде пряма, рівняння якої  . Знайдемо дві точки, що належать даній прямій. За умови
. Знайдемо дві точки, що належать даній прямій. За умови  або
або  (початкове значення об’єму) маємо
(початкове значення об’єму) маємо  . За умови
. За умови  або
або  (кінцеве значення об’єму) маємо
(кінцеве значення об’єму) маємо  . Пряма, що з’єднує ці дві точки і є графіком процесу в координатах
. Пряма, що з’єднує ці дві точки і є графіком процесу в координатах 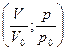 (див. рис. 16).
(див. рис. 16).
5) З першого пункту даного завдання отримаємо, що  . Тоді
. Тоді 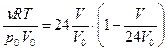 . Залежність
. Залежність  є квадратичною, отже її графіком буде парабола (див. рис. 17).
є квадратичною, отже її графіком буде парабола (див. рис. 17).
 Максимальне значення (як ми вже визначили у другому пункті) досягається при
Максимальне значення (як ми вже визначили у другому пункті) досягається при  і дорівнює
і дорівнює  . За умови
. За умови  маємо:
маємо:  ; при
; при  маємо:
маємо:  . Парабола, яка зображена на рисунку, і є графіком процесу в координатах
. Парабола, яка зображена на рисунку, і є графіком процесу в координатах  .
.
6. Заповніть пропуски у твердженнях, що наведені після рисунків:
 1 1
|  2 2
|  3 3
| |
 4 4
|  5 5
|   6 6
| |
 7 7
|  8 8
| ||
 9 9
|  10 10
| ||
1) Залежність 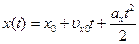 при деяких ненульових значеннях параметрів графічно подана на рис. ____. 2) Початкова координата
при деяких ненульових значеннях параметрів графічно подана на рис. ____. 2) Початкова координата  ___0. 3) Початкова швидкість
___0. 3) Початкова швидкість  ___0. 4) Прискорення
___0. 4) Прискорення  ___0. 5) Враховуючи, що
___0. 5) Враховуючи, що  , маємо
, маємо  =_________. 6) Графік
=_________. 6) Графік  поданий на рис. ____.
поданий на рис. ____.
7) Максимальне значення  досягається при
досягається при  ______.
______.
8) Максимальне значення  ____________. 9) При
____________. 9) При  ___________________, координата
___________________, координата  . 10) Дотична до графіка
. 10) Дотична до графіка  в точці (0;
в точці (0;  ) задається формулою
) задається формулою  _________.
_________.
Коментар. 1. Залежність  є квадратичною, тому її графіком є квадратична парабола, яка при деяких ненульових значеннях параметрів представлена на рис. 3.
є квадратичною, тому її графіком є квадратична парабола, яка при деяких ненульових значеннях параметрів представлена на рис. 3.
2. Початкова координата  , як видно з рис. 3.
, як видно з рис. 3.
3. На початку руху координата  зростає (див. рис. 3). Це означає, що проекція початкової швидкості на вісь
зростає (див. рис. 3). Це означає, що проекція початкової швидкості на вісь  додатна (
додатна ( ).
).
4. Гілки квадратичної параболи спрямовані вниз. Це означає, що коефіцієнт перед  від’ємний, тобто
від’ємний, тобто  .
.
5. Проекція швидкості на вісь  дорівнює похідній координати
дорівнює похідній координати  за часом:
за часом:  .
.
6. Функція  є лінійною. Отже, її графіком буде пряма. Враховуючи, що
є лінійною. Отже, її графіком буде пряма. Враховуючи, що  , обираємо рис. 10.
, обираємо рис. 10.
7. Максимальне значення  досягається тоді, коли
досягається тоді, коли  . Дійсно, при
. Дійсно, при  координата
координата  буде зростати, а при
буде зростати, а при  буде спадати. Таким чином,
буде спадати. Таким чином,  знаходиться з рівняння
знаходиться з рівняння 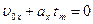 . Звідки
. Звідки  .
.
8. Максимальне значення координати можна знайти, підставивши вираз для  у вихідну формулу для
у вихідну формулу для  . Але існують й інші можливості. Наприклад, оскільки координата зростала у той час, коли проекція швидкості зменшувалася за лінійним законом від
. Але існують й інші можливості. Наприклад, оскільки координата зростала у той час, коли проекція швидкості зменшувалася за лінійним законом від  до нуля,
до нуля, 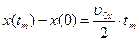 . Враховуючи значення
. Враховуючи значення 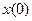 і
і  , отримуємо:
, отримуємо:  . Нагадаємо, що
. Нагадаємо, що  , тому, як і треба було очікувати,
, тому, як і треба було очікувати, 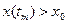 .
.
9. Щоб знайти  , треба розв’язати квадратичне рівняння і з отриманих коренів взяти додатний.
, треба розв’язати квадратичне рівняння і з отриманих коренів взяти додатний.

 .
.
Знак перед радикалом (позначкою квадратного кореня) обраний з урахуванням того, що  .
.
10. Дотична до графіка  в точці (0;
в точці (0;  ) є графіком рівномірного руху з початковою координатою
) є графіком рівномірного руху з початковою координатою  та швидкістю, що співпадає з початковою швидкістю розглядуваного рівноприскореного руху. Нагадаємо, що фізичний зміст похідної від функції полягає у тому, що вона є швидкістю зростання функції, а її геометричний зміст — у тому, що вона є кутовим коефіцієнтом дотичної до графіка функції. Таким чином,
та швидкістю, що співпадає з початковою швидкістю розглядуваного рівноприскореного руху. Нагадаємо, що фізичний зміст похідної від функції полягає у тому, що вона є швидкістю зростання функції, а її геометричний зміст — у тому, що вона є кутовим коефіцієнтом дотичної до графіка функції. Таким чином,  .
.
7. Впишіть термін за аналогією:
1) сила — потенціальна енергія
напруженість електричного поля — ____________
2) потужність — робота
сила струму — ______________
3) координата — заряд
швидкість — ______________
4) маса — індуктивність
імпульс — ________________
5) напруга — вольтметр
тиск — _________________
Коментар. 1) Потенціал  електричного поля так само пов’язаний з напруженістю електричного поля
електричного поля так само пов’язаний з напруженістю електричного поля  , як потенціальна енергія
, як потенціальна енергія 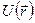 — з силою
— з силою  . Ці характеристики електричного поля вводяться таким чином, щоб для пробного точкового заряду його потенціальна енергія в електричному полі й сила, що на нього діє, обчислювалися за формулами:
. Ці характеристики електричного поля вводяться таким чином, щоб для пробного точкового заряду його потенціальна енергія в електричному полі й сила, що на нього діє, обчислювалися за формулами: 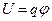 і
і  . Звернемо увагу на те, що для знаходження вірної відповіді ми не встановлювали, як саме пов’язані
. Звернемо увагу на те, що для знаходження вірної відповіді ми не встановлювали, як саме пов’язані  і
і  , або
, або  і
і  відповідно. Щоб у загальному випадку записати зв’язок між напруженістю електричного поля
відповідно. Щоб у загальному випадку записати зв’язок між напруженістю електричного поля  і потенціалом
і потенціалом  , треба використати математичні поняття, які виходять за рамки шкільної програми. Отже, і в університеті буде чим зайнятися!
, треба використати математичні поняття, які виходять за рамки шкільної програми. Отже, і в університеті буде чим зайнятися!
2) Потужність (мається на увазі механічна) — це швидкість виконання роботи, а сила струму (мається на увазі електричного) – це швидкість протікання електричного заряду через переріз провідника. Зверніть увагу на одиниці вимірювання: Вт=Дж/с, А=Кл/с.
3) Якщо координаті ставиться у відповідність заряд, то швидкості (у кінематичному розумінні) доречно поставити у відповідність силу струму. А на якій же підставі координаті ставиться у відповідність заряд? Тут треба згадати про аналогію, яку вивчали за шкільною програмою, між коливаннями координати  тягарця масою
тягарця масою  на пружині з коефіцієнтом жорсткості
на пружині з коефіцієнтом жорсткості  і коливаннями величини заряду
і коливаннями величини заряду  на конденсаторі ємністю
на конденсаторі ємністю  в електричному контурі, до якого крім конденсатора входить соленоїд з індуктивністю
в електричному контурі, до якого крім конденсатора входить соленоїд з індуктивністю  . У першому випадку відповідне диференціальне рівняння, що описує процес, має вигляд:
. У першому випадку відповідне диференціальне рівняння, що описує процес, має вигляд:
 .
.
А у випадку  контуру рівняння, з математичної точки зору, таке саме:
контуру рівняння, з математичної точки зору, таке саме:
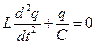 .
.
Як бачимо, у другому рівнянні  відіграє таку ж роль, що і
відіграє таку ж роль, що і  в першому. Якщо ж взяти від цих функцій похідні за часом, то отримаємо відповідно силу струму і швидкість (у кінематичному розумінні).
в першому. Якщо ж взяти від цих функцій похідні за часом, то отримаємо відповідно силу струму і швидкість (у кінематичному розумінні).
4) Після того, як ми згадали аналогію між диференціальними рівняннями, що описують коливання координати  і заряду
і заряду  , то зв’язок між масою
, то зв’язок між масою  та індуктивністю
та індуктивністю  стає очевидним. До речі, аналогом коефіцієнта жорсткості
стає очевидним. До речі, аналогом коефіцієнта жорсткості  буде величина обернена до ємності, тобто
буде величина обернена до ємності, тобто  . Тепер згадаємо, що імпульс (або кількість руху)
. Тепер згадаємо, що імпульс (або кількість руху)  (позначки векторів писати не будемо). Якщо
(позначки векторів писати не будемо). Якщо  замінити на
замінити на  , а
, а  на
на  , то отримуємо
, то отримуємо  , а це — магнітний потік
, а це — магнітний потік  (мова йде про власне магнітне поле соленоїда).
(мова йде про власне магнітне поле соленоїда).
5) Вольтметром вимірюють електричну напругу, а тиск вимірюють, наприклад, манометром. Назви інших приладів для вимірювання тиску також приймалися як правильні відповіді.
 2015-10-22
2015-10-22 409
409







