 Для изображения действительных чисел используются точки на числовой прямой. Комплексным числам соответствуют точки на координатной плоскости. Числу
Для изображения действительных чисел используются точки на числовой прямой. Комплексным числам соответствуют точки на координатной плоскости. Числу 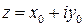 соответствует точка с координатами
соответствует точка с координатами  .
.
Каждой точке на плоскости ставится в соответствие радиус–вектор  .
.
Определение 1.4. Длину радиус–вектора  называют модулем комплексного числа
называют модулем комплексного числа  .
.
Угол 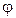 между радиус-вектором и положительным направлением оси
между радиус-вектором и положительным направлением оси  называют аргументом комплексного числа
называют аргументом комплексного числа  (рис.1.1.).
(рис.1.1.).
Модуль комплексного числа  обозначают
обозначают  , аргумент −
, аргумент −  . Аргумент комплексного числа определён с точностью до
. Аргумент комплексного числа определён с точностью до  ,
,  . Из определения следует, что
. Из определения следует, что  ,
,  ,
, 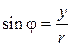 и
и  , т. е.,
, т. е.,  , тогда
, тогда 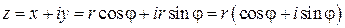 .
.
Определение 1.5. Выражение вида  называется тригонометрической формой комплексного числа.
называется тригонометрической формой комплексного числа.
Формулы Муавра
 ;
;
 , где
, где  .
.
1.1. Выполнить действия, ответ записать в алгебраической форме:
1.  . . | 2.  . . |
3.  . . | 4.  . . |
5.  . . | 6.  . . |
7.  . . | 8.  . . |
9.  . . | 10.  . . |
11.  , ,  , ,  , ,  . . | 12.  , ,  , , 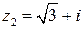 , ,  . . |
1.2. Решить уравнения и проверить подстановкой корней в уравнение:
1. 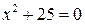 .
.
2.  .
.
3. 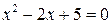 .
.
4.  .
.
5.  .
.
6.  .
.
1.3. Представить в тригонометрической форме комплексные числа:
| 1. 1. | 8. –1. | 15.  . . |
| 2. 5. | 9.  . . | 16.  . . |
| 3. –2. | 10. 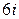 . . | 17.  . . |
4.  . . | 11.  . . | 18.  |
5.  | 12.  . . | 19.  . . |
6.  . . | 13.  . . | 20.  . . |
7.  . . | 14.  . . | 21.  . . |
1.4. Вычислить:
1.  . . | 4.  . . | 7.  . . |
2.  . . | 5.  . . | 8.  . . |
3. 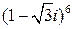 . . | 6.  . . | 9.  . . |
1.5. Найти все значения корней:
1.  . . | 4.  . . | 7.  . . |
2.  . . | 5.  . . | 8. 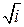 . . |
3.  . . | 6.  | 9. 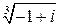 . . |
1.6. 1) Доказать, что сумма и произведение взаимно сопряженных комплексных чисел являются действительными числами.
2) Доказать равенства:
1.  .
.
2.  .
.
3.  ..
..
4.  .
.
1.7. Найти формулы для вычисления степеней числа i.
1.8. Найдите: 1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
1.9. Как расположены на комплексной плоскости: 1) сопряженные числа; 2) противоположные числа; 3) корни n -ой степени?
1.10 Решить уравнения:
1.  . . | 3.  . . | 5.  . . |
2.  . . | 4.  . . |
1.11. Решить уравнения:
1.  ;
;
2.  ;
;
3.  .
.
1.12. Где находится точка z комплексной плоскости, если точка  принадлежит мнимой оси?
принадлежит мнимой оси?
1.13. Найти действительные корни уравнения  .
.
КОМБИНАТОРИКА
Пусть дано множество  (все элементы различны). Обозначим произведение
(все элементы различны). Обозначим произведение  натуральных чисел
натуральных чисел  («эн факториал»). По определению
(«эн факториал»). По определению  .
.
Определение 1.8. Перестановкой из  элементов называется любое упорядоченное множество из этих
элементов называется любое упорядоченное множество из этих  элементов.
элементов.
Пример 1.3. Пусть  . Найти все перестановки.
. Найти все перестановки.
Решение.  . Их количество
. Их количество  .
.
Теорема 1.1. Число перестановок из  элементов равно
элементов равно 
Число перестановок обозначают  . Итак,
. Итак,  .
.
Пример 1.4. Сколькими способами можно разместить 5 гостей
1) в ряд;
2) за круглым столом.
Решение.
1) 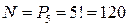 .
.
2) Зафиксируем одного гостя. Остальных упорядочим относительно выбранного  .
.
Определение 1.9. Размещением из  элементов по
элементов по  элементов называются перестановки по
элементов называются перестановки по  элементов, взятые из множества в
элементов, взятые из множества в  элементов. Обозначение числа размещений
элементов. Обозначение числа размещений  .
.
Теорема 1.2. Число размещений  .
.
Пример 1.5. Найти все размещения по 2 элемента из множества  .
.
Решение.  . Их количество
. Их количество 
Пример 1.6. Сколько четырёхбуквенных слов можно составить из 7 различных букв.
Решение. 
Определение 1.10. Сочетанием из  элементов по
элементов по  элементов называется любое неупорядоченное подмножество из
элементов называется любое неупорядоченное подмножество из  элементов множества в
элементов множества в  элементов.
элементов.
Число сочетаний обозначается  .
.
Пример 1.7. Дано  . Найти все сочетания по 2 элемента.
. Найти все сочетания по 2 элемента.
Решение. 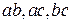 ;
;  . Порядок элементов нам не важен.
. Порядок элементов нам не важен.
Теорема 1.3. Число сочетаний 
Пример 1.8. Сколькими способами можно выбрать 3 дежурных из группы в 30 человек?
Решение.  .
.
1.14. Найдите: 1) 0!; 2) 5!; 3) 7!; 4)  ;5)
;5)  .
.
1.15. Сократите дробь: 1)  ; 2)
; 2)  .
.
1.16. Решить уравнение:  .
.
1.17. Найдите: 1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5)  .
.
1.18. Докажите, что  .
.
1.19. Докажите равенство:  ; 2.
; 2.  .
.
1.20. Докажите, что  .
.
1.21. В некотором царстве все люди отличаются набором зубов. Каково население этого царства?
БИНОМ НЬЮТОНА
Если  и
и  – числа, а
– числа, а  , то
, то

 . (1)
. (1)
Следствие 1.1.  , где
, где  – называют биномиальными коэффициентами.
– называют биномиальными коэффициентами.
Пример 1.9. Найти сумму биномиальных коэффициентов.
Решение. Положим в (1)  ,
,  , тогда
, тогда  .
.
Сумма биномиальных коэффициентов равна  .
.
Биноминальные коэффициенты можно найти из треугольника Паскаля

1.22. Разложите по биному:
1.  ; 2.
; 2.  ; 3.
; 3.  ; 4.
; 4.  ; 5.
; 5. 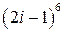 ; 6.
; 6.  .
.
1.23. Найдите: 1) пятое; 2) 10; 3) 15; 4) 16 слагаемое в разложении  .
.
1.24. Докажите, что
1)  ;
;
2) Сумма биномиальных коэффициентов, стоящих на четных местах, равна сумме биномиальных коэффициентов, стоящих на нечетных местах.
1.25. Пользуясь формулой Муавра и биномом Ньютона, выразить через степени  и
и  следующие функции кратных углов:
следующие функции кратных углов:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
 2015-10-22
2015-10-22 891
891







