КОМПЛЕКСНЫЕ ЧИСЛА. КОМБИНАТОРИКА. БИНОМ НЬЮТОНА.
Множество комплексных чисел (С)
Определение 1.1. Комплексным числом называется выражение вида  где
где 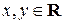 , а
, а  – мнимая единица, определяемая условием
– мнимая единица, определяемая условием  . При этом
. При этом  называют действительной частью
называют действительной частью  , а
, а  – мнимой частью комплексного числа
– мнимой частью комплексного числа 
 .
.
Определение 1.2. Запись  называется алгебраической формой комплексного числа.
называется алгебраической формой комплексного числа.
Операции над комплексными числами
Пусть  и
и 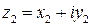 – два комплексных числа.
– два комплексных числа.
1. Равенство
Два комплексных числа равны, тогда и только тогда, когда равны их действительные и мнимые части, т. е.  , когда
, когда  ,
,  .
.
2. Сложение:  .
.
3. Умножение:  .
.
4. Сопряжение:  .
.
Сопряжение меняет знак перед мнимой частью комплексного числа.
Определение 1.3. Пару комплексных чисел  и
и  называют взаимно сопряжёнными числами.
называют взаимно сопряжёнными числами.
5. Деление:  .
.
Свойства операций
Пусть  комплексные числа.
комплексные числа.
1.  .
.
2.  .
.
3.  .
.
4.  .
.
5. 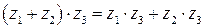 .
.
6.  .
. 
7.  .
.
8. 
9.  .
.
 2015-10-22
2015-10-22 351
351







