Определение
Минором 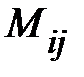 элемента
элемента 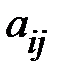 определителя
определителя
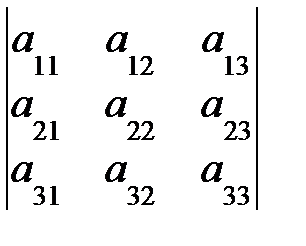
называется определитель, который получается из исходного путем вычеркивания i-й строки и j-го столбца, на пересечении которых данный элемент расположен.
Пример. Минор элемента 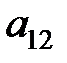 :
:
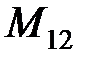 =
= 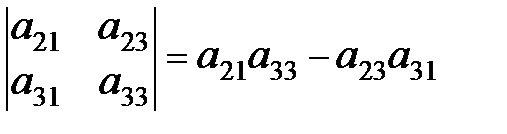
Определение
Алгебраическим дополнением 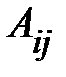 элемента
элемента 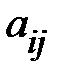 определителя называется выражение вида:
определителя называется выражение вида: 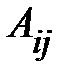 =
= 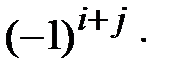
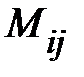 , где
, где 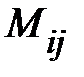 минор элемента
минор элемента 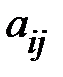 .
.
Пример. Алгебраическое дополнение элемента 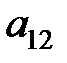 :
:
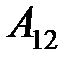 =
= 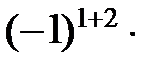
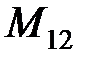 =
= 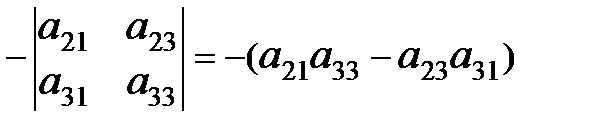
Утверждение. (Вычисление определителя)
Вычисление определителя может осуществляться путем разложения его по любой строке (столбцу) следующим образом,
по строке: 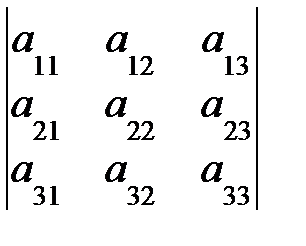 =
= 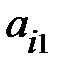
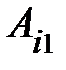 +
+ 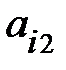
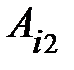 +
+ 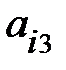
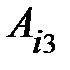 , (
, (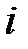 =1,2,3);
=1,2,3);
по столбцу: 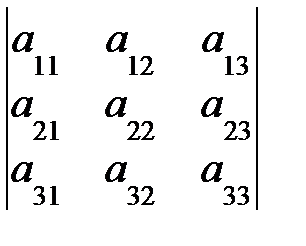 =
= 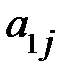
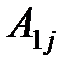 +
+ 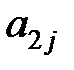
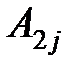 +
+ 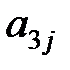
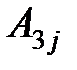 , (
, ( =1,2,3).
=1,2,3).
Пример. Разложение определителя по первой строке
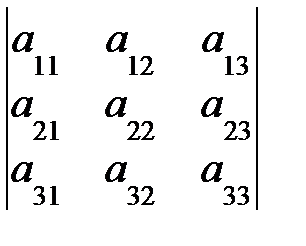 =
= 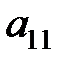
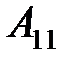 +
+ 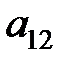
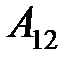 +
+ 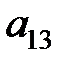
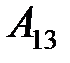 ;
;
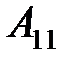 =
= 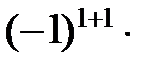
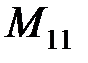 =
= 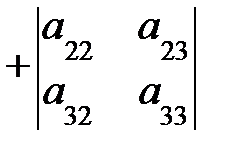 ;
;
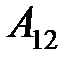 =
= 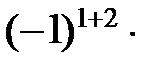
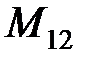 =
= 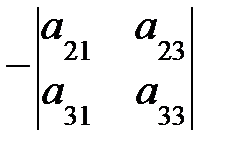 ;
;
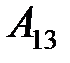 =
= 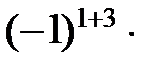
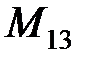 =
= 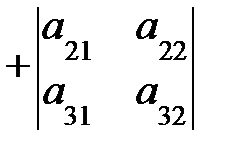 ;
;
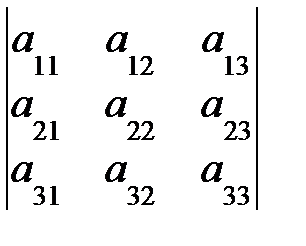 =
= 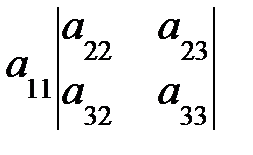
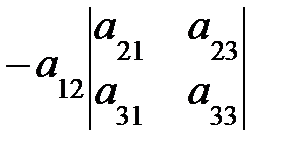
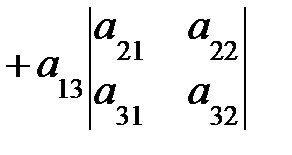 .
.
Пример. Вычисление определителя путем разложения по первой строке
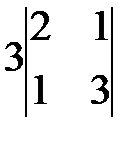
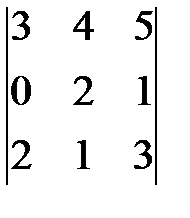 =
= 
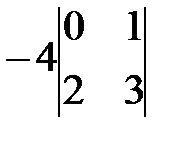
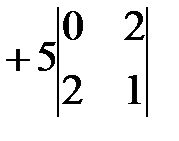 =
= 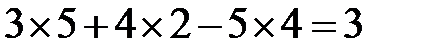 ;
;
Аналогично данный определитель можно разложить по любой другой строке (столбцу).
Пример. Определитель ступенчатой матрицы
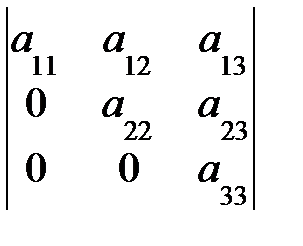 =
= 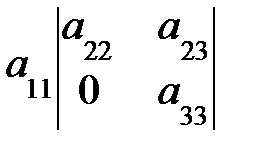
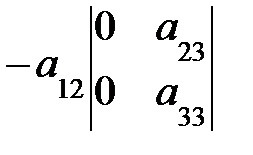
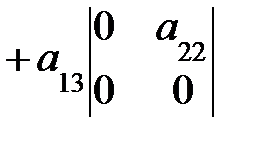 =
= 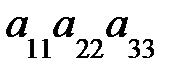 .
.
Утверждение Определитель ступенчатой матрицы равен произведению ее диагональных элементов.
Пример. Вычисление определителя путем приведения его к ступенчатому виду
В силу свойства №5, имеем:
 =
= 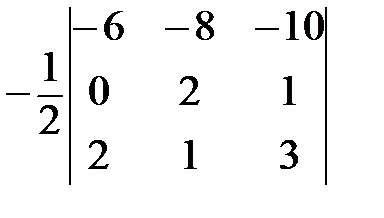 =
= 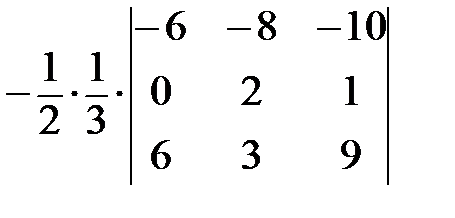 ;
;
Определитель не изменится, если к одной из его строк прибавить другую строку, умноженную на константу (см. утверждение 3), поэтому:
 =
= 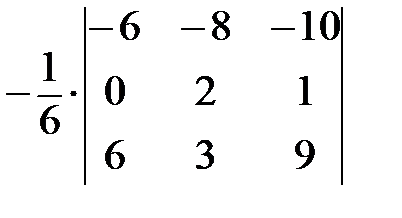 =
= 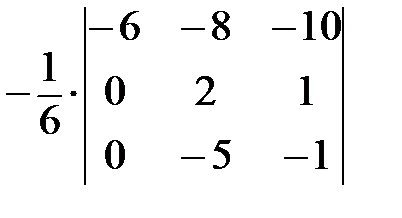 =
= 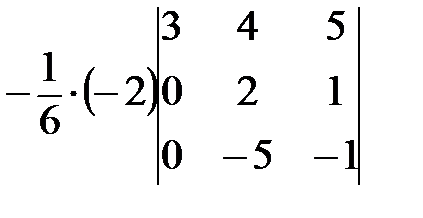 ;
;
 =
= 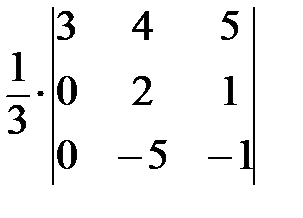 =
= 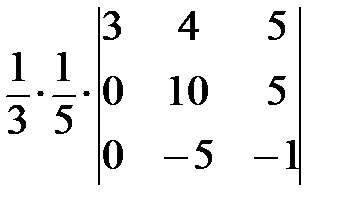 =
= 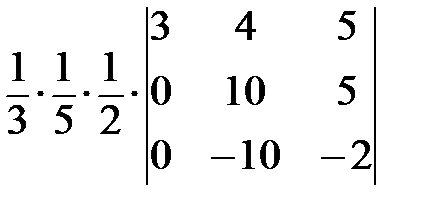 ;
;
 =
= 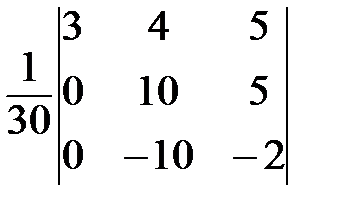 =
= 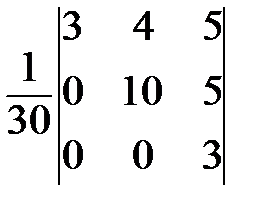 =
= 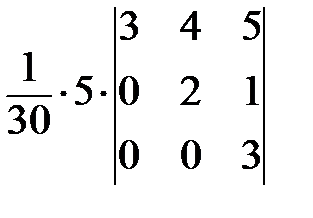 ;
;
 =
= 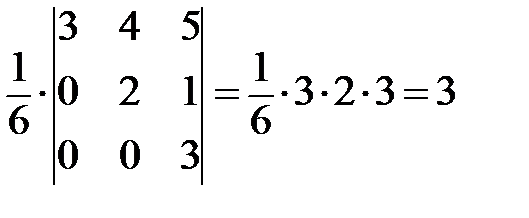 ;
;
 2015-10-22
2015-10-22 539
539







