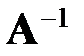2015-10-22
376
= 
где 
= 
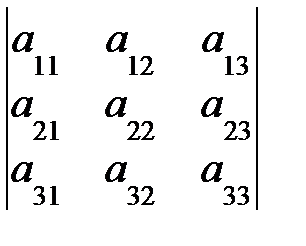- определитель матрицы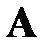 
- алгебраические дополнения элементов 
Пример. Вычислить матрицу 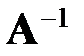, обратную матрице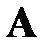
= 
= 
= 
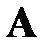= 30;
= 
= 
; 
= 
= 
;
= 
= 
; 
= 
= 
;
= 
= 
; 
= 
= 
;
= 
= 
;
= 
= 
; 
= 
= 
;
= 
= = 
= 
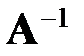Проверка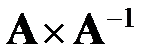 
= 
= 
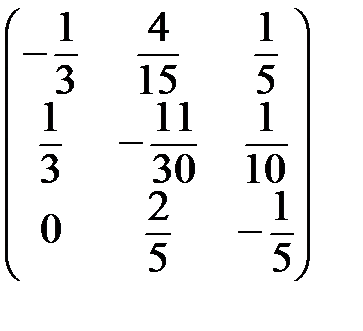Утверждение. (Критерий существования обратной матрицы)
Для существования 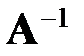необходимо и достаточно, чтобы det 
.
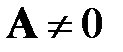Решение СЛУ с помощью обратной матрицы
СЛУ
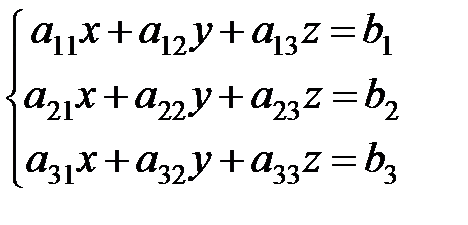
может быть представлена в виде 
= 
(см. пример №16)
где
матрица системы
столбец неизвестных 
столбец свободных членов.
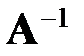
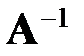
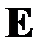
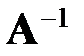
= ó = ó 
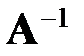
= ó = ó 
= 
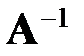
Пример. Решить СЛУ с помощью обратной матрицы
Матричный вид системы:
= 
ó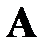 
= 
=
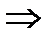
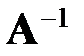
где = , = , = , =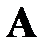
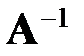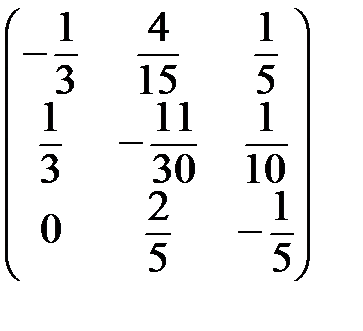
тогда = = = 
= 
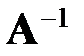
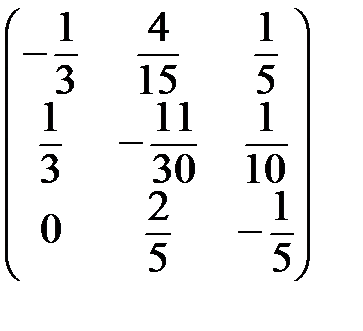
. Ответ: (1,2,3).
