Определение. Число  называется пределом последовательности
называется пределом последовательности  , если для любого положительного числа
, если для любого положительного числа  найдется член последовательности такой, что все члены последовательности
найдется член последовательности такой, что все члены последовательности  , следующие за ним, отстоят от
, следующие за ним, отстоят от  меньше, чем на
меньше, чем на  .
.
Определение. Число  называется пределом последовательности
называется пределом последовательности  , если в любом открытом промежутке, содержащем число
, если в любом открытом промежутке, содержащем число  , содержатся все члены
, содержатся все члены
последовательности  , начиная с некоторого.
, начиная с некоторого.
Теорема (о единственности предела). Если  — предел последовательности
— предел последовательности  и
и  — предел последовательности
— предел последовательности  , то
, то 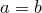 .
.
Доказательство. Предположим, что  . Возьмем
. Возьмем  . Найдется такой номер
. Найдется такой номер  , что
, что 

также существует 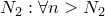

Возьмем 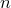 , которое больше
, которое больше  и
и 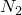 . Тогда
. Тогда

Обозначение.  есть предел
есть предел  :
:
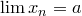 ,
,
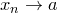 —
—  стремится (сходится) к
стремится (сходится) к  ,
,

Определение. Последовательность, имеющая предел, называется сходящейся.
Определение. Последовательность называется строго возрастающей (возрастающей) [ строго убывающей ]  убывающей
убывающей  , если каждый ее член, начиная со второго, больше (не меньше) [меньше]
, если каждый ее член, начиная со второго, больше (не меньше) [меньше]  не больше
не больше  предыдущего члена.
предыдущего члена.
Последовательности (строго) возрастающая и (строго) убывающая называются (строго) монотонными.
|
|
|
Определение. Последовательность  называется ограниченной, если существует
называется ограниченной, если существует  .
.
Теорема. Всякая сходящаяся последовательность ограничена.
Доказательство. Пусть  — предел последовательности
— предел последовательности  . Тогда найдется такой номер
. Тогда найдется такой номер  , что
, что 


Тогда  .
.
Замечание. Тем самым, мы доказали ограниченность последовательности  , поскольку, выбрав
, поскольку, выбрав  , получим
, получим  .
.
Определение. Говорят, что последовательность  отделена от нуля, если найдется такое положительное число
отделена от нуля, если найдется такое положительное число  , что все члены этой последовательности по модулю больше
, что все члены этой последовательности по модулю больше  .
.
Теорема (о предельном переходе в неравенствах). Пусть  и
и 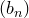 — последовательности, причем
— последовательности, причем 

 . Пусть
. Пусть  ,
,  . Тогда
. Тогда  .
.
Доказательство. Предположим, что утверждение теоремы неверно, т.е.  . Рассмотрим промежутки
. Рассмотрим промежутки

Возьмем  . Тогда
. Тогда 
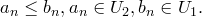
Получили противоречие, т.к.
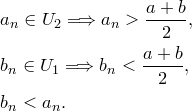
Замечание. Если в условии теоремы заменить неравенство  на
на  , то все равно можно утверждать лишь то, что
, то все равно можно утверждать лишь то, что  . Действительно,
. Действительно,

Теорема (принцип сжатой последовательности, теорема о двух милиционерах). Пусть даны последовательности  и существует
и существует  :
: 
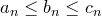 . Известно, что
. Известно, что 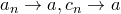 . Тогда
. Тогда  .
.
Доказательство. Возьмем произвольный промежуток  .
.

Обозначим  . Тогда
. Тогда 

Значит,  .
.
Замечание. Принцип сжатой последовательности является теоремой существования и не следует из теоремы о предельном переходе в неравенствах.
Определение. Говорят, что  , если
, если 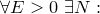

Последовательность  при этом называется бесконечно большой;
при этом называется бесконечно большой;
 , если
, если 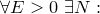

 , если
, если 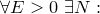

Определение. Последовательность  называется бесконечно малой, если
называется бесконечно малой, если  .
.
Задачи.
1) Выясните, являются ли последовательности монотонными
1. 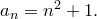
2. 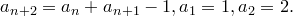
2) Выясните, являются ли последовательности ограниченными
|
|
|
1. 
2. 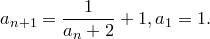
3) Последовательность  ограничена, а последовательность
ограничена, а последовательность 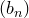 неограничена. Выясните, какие из следующих последовательностей обязательно неограниченные, а какие могут быть неограниченными:
неограничена. Выясните, какие из следующих последовательностей обязательно неограниченные, а какие могут быть неограниченными:
1. 
2. 
3. 
3) Докажите, что следующие последовательности стремятся к нулю:
1. 
2. 
4) Докажите, что
1. 
2. 
5) Приведите, если это возможно, примеры последовательностей, удовлетворяющим данным ниже условиям. Если это невозможно, объясните, почему.
1.  и
и  — расходящиеся,
— расходящиеся,  .
.
2.  — сходящаяся,
— сходящаяся,  — расходящаяся,
— расходящаяся,  — сходящаяся.
— сходящаяся.
3.  и
и  — расходящиеся,
— расходящиеся,  — сходящаяся.
— сходящаяся.
4.  и
и  — расходящиеся,
— расходящиеся, 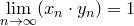 .
.
 2015-10-22
2015-10-22 716
716







