Складність алгоритмів

Природно, що перед розробкою програми слід придумати, як розв'язати поставлену задачу. При розробці алгоритму необхвдно, перш за все, приділити увагу часу його роботи й обсягу пам'яті, яку необхідно витратити для зберігання й обробки даних. Дані поділяють на вхідну інформацію (вхідне слово), ті, що вимагають проміжного зберігання, і вихідну інформацію (вихідне слово). Не всі дані вимагають одночасного зберігання й використання, а тому можна планувати роботу з ефективного їх використання.

Для розв'язання задачі можна написати багато різних алгоритмів. Чим вони відрізняються, який краще використовувати? Як визначити поняття "краще"? Такі питання виникають (або мають виникати) у професійного програміста.

Для початку замінимо поняття "краще" на "ефективніше" й далі його використовуватимемо. Ефективність програми є дуже важливою її характеристикою. Вона має дві складові: розмір і час.

Розмір вимірюється обсягом пам'яті, що вимагається для виконання програми. Іноді обсяг необхідної пам'яті є домінуючим фактором в оцінці ефективності програми. Проте останніми роками ця складова ефективності поступово втрачає своє значення.

Тимчасова ефективність програми визначається часом, необхідним для її виконання. Вона залежить як від конкретної реалізації алгоритму, так і від власне вибраного алгоритму для розв'язання поставленої задачі.

Отже, складність обчислення, тобто роботи алгоритму на певному вхідному слові, визначається ресурсами, а ресурс, необхідний для конкретного обчислення, – це число. Знаходженням та оцінкою такого числа ми й займемося.

Основною властивістю алгоритму є виконання поставленої задачі за скінченну кількість кроків. Швидкість, з якою алгоритм виконується на конкретному пристрої, може істотно залежати від набору вхідних даних. При цьому швидкий у середньому алгоритм здатний давати збої в окремих "поганих" випадках. І, якщо задача має напевно розв'язуватися за певний час роботи процесора, то ми віддамо перевагу алгоритму, повільнішому в середньому, проте надійному в гірших ситуаціях. Саме уміння передбачати погані ситуації і відрізняє кваліфікованого алгоритміста від звичайного кодувальника.

Будь-який крок алгоритму реалізується деякою кількістю машинних операцій. Деталізація алгоритму має бути такою, щоб на кожному окремому кроці не потрібне було його подальше алгоритмічне опрацьовування. Тут можливі лише дві ситуації: або фіксований час виконання такого кроку визначено деяким набором простих, без циклів, команд мови програмування, або йдеться про ускладнений крок, для якого відповідний аналіз уже проводився і результати відомі.

Тепер перейдемо до головного питання, яке можна задати будь-якому програмісту: припинить його програма своє виконання або ж працюватиме до нескінченності? За теоремою, доведеною Тьюрінгом у 30-ті рр. XX ст., не існує алгоритму, що дає відповідь на це питання, тобто проблема зупинки нерозв'язна. Таким чином, навіть якщо ми маємо алгоритм, який розв'язує поставлену задачу, то ще не відомо, чи приведе він нас до відповіді. Тому нас цікавить не просто існування алгоритмів для нашої задачі, а й їх ефективність. Причому з усіх складових ефективності ми звертатимемо особливу увагу на час (швидкодію) роботи алгоритму. Справедливою, хоч і з деякими обмовками, є така формула:

(загальний час роботи)=(кількість операцій алгоритму)*(час на 1 операцію)

Поліпшення обох членів у правій частині формули здійснюється незалежно. Грубо кажучи, програми відповідають за перший співмножник, а процесори – за другий.

Розглянемо деякі приклади.

1. Алгоритм обміну значень двох змінних цілого типу – а і b – реалізується в загальному випадку за три кроки, незалежно від того, до якого типу простих даних він застосовується:

temp=а

а=b

b=temp

Якщо застосуємо для обміну значеннями алгоритм, що використовує арифметичні операції, то дістанемо таку послідовність дій:

a=a+b

b=a-b

a=a - b

При цьому отримаємо ті самі три кроки.

2. Знайти суму натуральних чисел від 1до заданого n.

Якщо скористатися відомою формулою для суми арифметичної прогресії, то для обчислення також знадобляться лише три кроки: додавання, множення й ділення. Якщо ж реалізувати обчислювальний процес як циклічний (цикл із параметром), і керувальна змінна пробіжить значення від 1до n, то доведеться виконати n кроків алгоритму.

Сумнівів, який з алгоритмів ефективніший, здається, не виникає.

Для алгоритмів, подібних до щойно розглянутого (n кроків для обробки n вхідних значень), кількість кроків є функцією від кількості елементів, що обробляються, – g (n). Не для кожного алгоритму таку функцію можна знайти й обчислити.

Для оцінки швидкості зростання досліджуваної функції порівняємо її з функцією, дія якої вже добре відома. При дослідженні поведінки функцій g (n) натурального n розглядатимемо такі функції g (n), що зростають не швидше f (n), тобто існує така пара додатних значень M і n ₀, що ½g(n)½ £ M½ f (n₀)½ для n ³ n₀. Або можна сказати, що функція g (n) має порядок f (n) для великих n. Таку залежність позначають у математиці символом О.

Укажемо кілька важливих властивостей O-оцінювання:

1. f (n)= O (f (n)).

2. c · O (f (n))= O (f (n)), де с – деяка константа.

3. О (f (n))+ O (f (n))= O (f (n)).

4. О (О (f (n)))= O (f (n)).

5. О (f (n)) ·О (g (n))= O (f (n) ·g (n)).

6. О (k * f )= O (f ), де k – деяка константа.

7. О (f + g) дорівнює домінанті О (f ) і О (g).

Тут с, n позначають константи, а f і g – функції.

Можна сказати, що ефективність алгоритму безпосереднього підсумовування n елементів відповідає лінійній складності, оскільки його швидкодія, тобто кількість кроків, згідно із властивістю 1 становить О(n).

Розглянемо таку задачу: для набору з n попарно нерівних відрізків підрахувати кількість усіх трійок, з яких можна отримати невироджені трикутники.

Треба перевірити n (n – 1)(n – 2) варіантів, що відповідає кубічній складності О (n ³).

У загальному випадку, якщо ефективність алгоритму визначається обчислювальною складністю обробки багаточлена порядку к, то часто задовольняються оцінкою О (n^k), не зважаючи, згідно з властивістю 2, на старший коефіцієнт і решту членів полінома.

О -оцінювання дозволяє не використовувати конкретний обчислювальний пристрій для аналізу складності.

Нехай є деяка віртуальна машина М, яка обчислює функцію f, і визначені вхідні дані: х – деяке двійкове слово. Визначимо функцію Т (М, х) як кількість операцій, що потрібні машині М для роботи на вхід­ному слові х. Справедлива така теорема.

Теорема (Блюм, 1971). Існує така обчислювана функція f, що будь-яку машину М, яка її обчислює, можна прискорити так: існує інша машина що також обчислює f, дляякої виконується нерівність для майже всіх n,де .

Теорема в наведеному формулюванні справедлива не для всіх функцій. За більш вільного формулювання скажімо так: неможливо придумати найкращий алгоритм, оскільки існує ще швидший.

Складність задач

Поняття складності алгоритму пов'язане з поняттям складності задачі. Із теореми Блюма можна зробити висновок, що визначати склад­ність задачі через складність найкращого алгоритму для її розв'язання – не найвдаліший спосіб.

Нехай необхідно побудувати алгоритм для розв'язання такого класу задач: обчислити значення виразу у точці x = b, де a_i ÎR, b Î R,а R – множина дійсних чисел.

Множина вхідних даних: де a_i Î R, b ÎR, – вектор з n +1 дійсних чисел, b – дійсне число.

Результат: , де .

Змінні: i – цілого типу; х, r – дійсного.

Константи:{ a_i ½ i = 0,..., n }, п.

Наведемо алгоритм для даного класу задач:

Алгоритм:

1. Покласти iрівним n, s рівним 0, хрівним b .

2. Піднести хдо степеня i .

3. Помножити на степінь.

4. Покласти sрівній сумі sі добутку на степінь.

5. Якщо i=0, то s – результат (стоп).

Інакше покласти i=i - 1, перейти до кроку 2.

Послідовність обчислень за алгоритмом описує вираз

.

Існує також інший алгоритм для розв'язання задач цього класу.

Вхідні дані:ті самі, що й у попередній задачі.

Результат: такий самий.

Змінні: r, s, x – дійсного типу, i – цілого типу.

Константи: п.

Алгоритм:

1. Покласти iрівним п,x рівним b.

2. Покласти rрівним

3. Помножити rна x .

4. Покласти rрівним добутку.

5. Покласти iрівним i – 1 .

6. Покласти rрівним r+ .

7. Якщо i=0, то r – результат, інакше перейти до кроку 3.

Послідовність обчислень за цим алгоритмом можна пояснити виразом

.

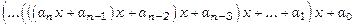Такий метод обчислення значення полінома у точці називається схемою Горнера.

Виразимо складність дії піднесення до степеня i як (i – 1)операцій множення. Тоді складність другого алгоритму (за схемою Горнера) у вигляді кількості операцій додавання та множення дорівнюватиме 2 п,а для прямого алгоритму становитиме

Таким чином, другий алгоритм ефективніший за перший.

Тепер можна дати визначення ефективному алгоритму.

Означення 1.7. Алгоритм, трудомісткість якого обмежена поліномом від характерного обсягу задачі, називається ефективним.

Під складністю задачі розумітимемо час, необхідний для обчислення функції, за допомогою якої знаходиться її розв'язок. Під складністю розумітимемо складність алгоритму у найгіршому випадку. Ос­кільки не можна побудувати для кожної функції найкращої машини, що її обчислює, то введемо поняття класу складності.

Означення 1.8. Клас складності містить функції f, для яких існує машина М, що обчислює f,така, що функція Т (М, х) за часом обмежена функцією t (n) із точністю до мультиплікативної константи, тобто

,

де t (n) – порядок класу.

Класом задач складності t (n) назвемо сукупність задач, які розв'язуються за час порядку t (n).

O- оцінки виражають відносну швидкість алгоритму залежно від початкових даних. Розглянемо класи O-складності алгоритмів. Нехай N – кількість оброблюваних даних (табл. 1.1).

Таблиця 1.1

Класи складності	Опис програм
О (1)	Більшість операцій у програмі виконується або один раз, або фіксовану кількість разів. Будь-який алгоритм, що завжди вимагає (незалежно від обсягу даних) одного й того самого часу, має константну складність.
О (N)	Час роботи програми лінійно залежить від N. Властиво алгоритмам, які обробляють кожен елемент вхідних даних кількість разів, пропорційну лінійній функції.
О (N 2), О (N 3), О (Nк)	Поліноміальна складність. О (N 2) – квадратична складність, О (N 3) – кубічна складність. Час роботи програми пропорційний поліноміальній функції.
О (Log(N))	Час роботи програми логарифмічний. Зустрічається зазвичай у програмах, які ділять велику задачу на маленькі й розв'язують їх окремо.
О (N *log(N))	Такий час роботи мають алгоритми, які ділять велику задачу на маленькі, а потім, розв'язавши їх, сполучають розв'язки.
О (2 N)	Експоненціальна складність. Такі алгоритми найчастіше виникають унаслідок підходу, що має назву "метод грубої сили".

Розглянемо прийоми проведення аналізу алгоритмів і визначення їх складності. Тимчасова складність алгоритму може бути порахована, виходячи з аналізу його керувальних структур. Ми пам'ятаємо, що до керувальних структур належать лінійні та умовні вирази, цикли (табл. 1.2).

Таблиця 1.2

Керувальна структура	Складність
Простий вираз	О (1)
Лінійний вираз S 1,… Sn	Домінанта О (С 1),…, О (Cn), де C 1,…, Сn – складність обчислення виразів S 1,… Sn
Якщо <умова> то дія1 Інакше дія2	Домінанта О (С 1), О (С 2), О (С 3), де С 1, С 2, С 3 – складність обчислень дій та умови, відповідно
Цикл із n повтореннями тіла S 1	О (n * C 1), де С 1 – складність обчислення S 1

Якщо немає рекурсії й циклів, то всі керувальні структури можуть бути зведені до структур константної складності. Отже, і весь алгоритм також характеризується константною складністю. Тому визначення складності алгоритму в основному зводиться до аналізу циклів і рекурсивних викликів.

Розглянемо алгоритм обробки елементів масиву.

Алгоритм:

Для i=1 до N виконувати

Початок

{Простий вираз}

кінець;

Складність цього алгоритму становить О (N), оскільки тіло циклу виконується N разів, а складність тіла циклу дорівнює О (1).

Якщо один цикл вкладено в іншій та обидва мають однакову кількість повторень, то вся конструкція характеризується квадратичною складністю.

Розглянемо алгоритм.

Алгоритм:

Для i=1 до N виконувати

Для j=1 до N виконувати

Початок

{Простий вираз}

кінець;

Його складність становить О (N 2).

Оцінимо складність алгоритму, що має назву "Трійки Піфагора". Суть задачі: знайти всі трійки натуральних чисел (х, y, z), що задо­вольняють рівняння x ² + y ² = z ². Піфагор знайшов формули, які в сучасному формалізмі можна записати як

x =2 п +1, y =2 п (п +1), z =2 п ²+2 п +1,

де п – ціле число. Наприклад:

А	B	С

Трикутники із такими сторонами є прямокутними. Розпочате Піфагором дослідження рівняння x ²+ y ²= z ² привело до складної проблеми сучасної теорії чисел – дослідження у цілих числах рівняння xⁿ + yⁿ = zⁿ. Перед аналізом складності програми, яка знаходить трійки Піфагора, зазначимо, що існують два способи аналізу складності: висхідний (від внутрішніх керувальних структур до зовнішніх) і низхідний (від зовнішніх – до внутрішніх). Ми користуватимемося висхідним. Розглянемо алгоритм.

Алгоритм:

D	А		Вхід: n 1. small=1
E		2. Поки small<n виконувати Початок
B		3. next=small
G		4. Поки next<=n виконувати Початок
С		5. last=next
I		6. Поки last<n виконувати Початок
F		7. Якщо last<=2*small і next<=2*small і last*last=small*small+next*next
H	8. то друк(small) друк(next) друк(last)
J		9. last=last+1 кінець циклу last
К		10.next=next+1 кінець циклу next
	11.small=small+1 кінець циклу small
	12. Кінець Вихід: роздруковані значення small,next,last

Підрахуємо його складність:

О (H) = O (1) + O (1) + O (1) = O (1);

О (I) = O (N)*(О (F) + O (J)) = O (N)* O (домінанти умови) = О (N);

О (G) = O (N)*(О (C) + O (I) + O (K)) = O (N)*(О (1) + O (N) + O (1)) = O (N 2);

О (E) = O (N)*(О (B) + O (G) + O (L)) = O (N)* О (N 2) = О (N 3);

О (D) = O (A) + O (E) = O (1) + О (N 3) = О (N 3).

Таким чином, складність алгоритму становить О (N 3).

Проаналізувавши програму, можна дійти висновку, що основну оцінку складності забезпечують вкладені цикли. Тому для зменшення складності, перш за все, можна спробувати зменшити глибину вкладеності циклів. Далі слід розглянути можливість скорочення кількості операторів у циклах з найбільшою глибиною вкладеності. Однак ці рекомендації не завжди можна виконати.

Оцінимо алгоритм бінарного пошуку ключа в упорядкованому масиві. Суть алгоритму: розглядаємо серединний елемент масиву й перевіряємо відповідність ключа до його значення. Якщо не вдається знайти відповідність, то порівнюємо ключ і значення серединного елемента, а потім переміщаємося в нижню половину списку елементів масиву, якщо ключ менше, і верхню – якщо більше. В обраній половині знову шукаємо середину та знову порівнюємо із ключем. Якщо не виходить, то знову ділимо надвоє поточний інтервал.

Розглянемо детальніше алгоритм. Вхід: low, high – змінні, що задають нижню й верхню межі масиву, key – шукане число.

Початок

поки low<=high виконувати

Початок

mid=(low+high)/2;

data=a[mid];

якщо key=data

тоді початок search=mid; закінчити роботу кінець

інакше якщо key<data

то high=mid-1

інакше low=mid+1;

кінець;

search=-1;

кінець;

Перша ітерація циклу має справу з усім списком елементів. Кожна подальша ітерація ділить список навпіл. Наприклад, розмірами списків для послідовних кроків алгоритму є n n /2¹ n /2² n /2³ n /2⁴ ... n /2 ^m. Урешті-решт знайдеться таке ціле m, що n /2 ^m <2 або n < 2 ^{m+ 1}. Оскільки m – перше ціле, для якого n /2 ^m < 2, то має бути вірним n /2 ^m – 1 > = 2 або 2 ^m = < n. Із цього випливає, що 2 ^m = < n < 2 ^m +1.

Візьмемо логарифм кожної частини нерівності й дістанемо m =< log₂(n) = x < m + 1. Значення m – найбільше ціле, що менше або дорівнює х. Отже, складність дорівнює О (log₂ n).

Знайдемо вираз для часу, що необхідний програмі для обробки масиву з N елементами як функцію від N. Зазвичай нас цікавить середній випадок – очікуваний час роботи програми на типових вхідних даних, і гірший – очікуваний час роботи програми на найгірших вхідних даних.

Через труднощі, пов'язані з проведенням аналізу часової складності алгоритму в середньому, часто доводиться задовольнятися оцінками для гіршого й кращого випадків. Ці оцінки, по суті, визначають нижню й верхню межі складності в середньому. У такому разі оцінка, одержана для найгіршого випадку, може служити хорошою апроксимацією складності в середньому.

Основним недоліком O -оцінювання є його надмірна грубість. Якщо алгоритм А виконує деяку задачу за 0.001* N, тоді як для її розв'язання за допомогою алгоритму В потрібно 1000* N з, то В у мільйон разів швидше за А. Однак А та В мають одну й ту саму складність О (N).

Можна умовно розділити задачі на прості, які мають поліноміальний час розв'язання (розв'язання системи лінійних алгебраїчних рівнянь у раціональних числах); складні (важкі, що не мають розв'язку) – задачі, які не розв'язуються за поліноміальний час, або алгоритм розв'язання за поліноміальний час не знайдений. Крім цього, існують принципово нерозв'язні задачі. Дане твердження доведене А. Тьюрінгом.

Завершимо розгляд основ теорії складності тезами двох великих учених.

Теза Колмогорова. Проблеми, які не можуть бути розв'язані без пов­ного перебирання, залишаться за межами можливостей машини на скільки завгодно високому рівні техніки й культури.

На думку А. Тьюрінга, усе те, що природно визнали б обчислюваним, могло б, принаймні у принципі, бути обчислене у природі. Тому справедлива

Теза Тьюрінга. Можливо побудувати генератор віртуальної реальності з репертуаром, що включає всі середовища, існування яких не суперечить законам фізики. Це означає наявність:

a відповідної програми;

a необхідних обчислювальних ресурсів (швидкодії, обсягу пам'яті).

Завдання для самостійної роботи

1. Навести визначення алгоритму.

2. Навести властивості алгоритму.

3. Навести класифікацію внутрішніх структур алгоритму.

4. Що таке складність задачі, алгоритму?

5. Навести тези Тьюрінга, Колмогорова.

6. Як обчислювати складність задачі, алгоритму?

Форма Бекуса – Наура

Основи сучасного програмування Основи сучасного програмування Основи сучасного програмування Основи сучасного програмування Основи сучасного програмування Основи сучасного

Великої уваги потребують проблеми формалізації опису синтаксису мови програмування. Вдалий формалізм дозволяє не тільки описувати мови, але й спрощувати роботу зі створення компіляторів.

Мова, що використовується для формалізації синтаксису іншої мови, називається метамовою. Її граматика містить правила виведень, що визначають синтаксис мови, або, іншими словами, допустимі компоненти й конструкції ланцюжків мови. Для задання правил використовуються різні форми опису: символічна, форма Бекуса – Наура (БНФ), ітераційна й синтаксичні діаграми.

При розгляді загальних властивостей граматик зазвичай застосовують символічну форму задання правил. Вона використовує як елементи нетермінального словника окремі символи та стрілки у вигляді роздільників правої й лівої частин правила.

При описі синтаксису конкретних мов програмування доводиться вводити велику кількість нетермінальних символів, тому символічна форма запису втрачає свою наочність.

У теперішній час найуживанішою для опису синтаксису мов програмування є метамова БНФ. Ідея цієї метамови полягає у структуруванні понять вихідної мови програмування й визначенні складніших понять через простіші. Будь-яке поняття зображується своїм найменуванням у кутових дужках: <...>. Речення БНФ є одним визначенням деякого поняття через інші у формі

поняття, знак"::=", після якого записується визначення поняття

У складі визначення можуть використовуватися інші поняття, сим­воли алфавіту, ключові слова мови програмування, а також спеціальні символи мови БНФ, що мають визначений сенс. Як такі символи використовуються вертикальна риска й круглі, квадратні та фігурні дужки. Їхнє використання підкоряється правилам:

a запис <поняття1>::<поняття2><поняття3> і т. д. означає, що перше поняття є послідовним записом інших понять;

a запис <поняття1>::=<поняття2>|<поняття3>| і т. д. означає, що пер­ше поняття збігається з одним з інших;

a круглі дужки використовуються для групування складних кон­струкцій БНФ усередині простих (допоміжний інструмент, можна не використовувати);

a узяття у квадратні дужки частини визначення свідчить про необов'язковість цієї частини;

a узяття у фігурні дужки частини визначення свідчить про те, що ця частина може бути повторена довільну кількість разів (або не повторюватись жодного разу);

a замість складного поняття до БНФ можуть входити термінальні символи й ключові слова.

Наведемо кілька прикладів.

1. Непорожній список, що складається із довільної кількості елементів, розділених комами, описується як

<список>::=<елемент списку>{, <елемент списку>}

2. Якщо список може бути порожнім, то його опис виглядатиме як

<список>::=|<елемент списку>{, <елемент списку>}

3. Ідентифікатор – це послідовність літер і цифр, що починається з літери

<ідентифікатор>::=<літера>{<літера>|<цифра>}

Більшість символів у мовах програмування потрапляють в один із таких класів:

a ідентифікатори;

a службові слова (які є підмножиною ідентифікаторів);

a цілі числа;

a однолітерні роздільники (+, – (,), / і т. д.);

a дволітерні роздільники (//, /*, **,: = і т. д.).

Ці символи можна описати простими правилами:

<ідентифікатор>::=<літера>|<ідентифікатор>

<літера>|<ідентифікатор><цифра>

<ціле>::=<цифра>|<ціле><цифра>

<роздільник>::=+|–|(|)|/|...

<роздільник>::=<SLASH>/|<SLASH>*|<AST>*|<COLON>=

<SLASH>::=/

<AST>::=*

<COLON>::=:

Завдання для самостійної роботи

1. Написати БНФ цілого числа.

2. Написати БНФ числа із плаваючою точкою.