Знакопеременные ряды. Абсолютная и условная сходимость числовых рядов

Числовой ряд называется знакопеременным, если положительные и отрицательные члены ряда не обязательно чередуются между собой. Знакочередующийся ряд является частным случаем знакопеременного ряда.

Для знакопеременных рядов имеет место следующий общий достаточный признак сходимости.

Теорема. Если сходится числовой ряд, составленный из модулей членов знакопеременного ряда то сходится и сам знакопеременный ряд ..

Доказательство. Пусть дан знакопеременный ряд ..

Рассмотрим вспомогательный ряд, составленный из членов ряда и :

Поскольку 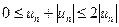для всех , а ряд сходится в силу условия теоремы и свойства числовых рядов, то на основании первой теоремы сравнения сходится и ряд . Поскольку исходный знакопеременный ряд представляет собой разность двух сходящихся рядов , то на основании свойства числовых рядов он сходится.

Следует заметить, что из сходимости числового ряда не следует сходимость ряда .

Знакопеременный ряд называется абсолютно сходящимся, если ряд, составленный из модулей его членов , сходится.

Знакопеременный ряд называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов , расходится.

Пример 2. Исследовать сходимость ряда .

Решение: Для данного знакочередующегося ряда выполняются условия признака сходимости Лейбница: члены ряда монотонно убывают по абсолютной величине , предел общего члена ряда стремится к нулю. Поэтому, указанный ряд сходится. Однако ряд, составленный из модулей членов данного ряда , расходится как гармонический ряд.