Абсолютно сходящиеся ряды среди знакопеременных рядов занимают особое место, поскольку наследуют основные свойства конечных сумм (переместительность, сочетательность, распределительность).
Приведем в виде теорем основные свойства абсолютно сходящихся рядов.
Теорема Дирихле. Если ряд абсолютно сходится и имеет сумму  , то ряд, полученный из него перестановкой членов, также сходится и имеет ту же сумму
, то ряд, полученный из него перестановкой членов, также сходится и имеет ту же сумму  , что и исходный ряд.
, что и исходный ряд.
Теорема о сумме абсолютно сходящихся рядов. Абсолютно сходящиеся ряды  и
и 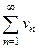 с суммами
с суммами 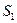 и
и  можно почленно складывать. В результате получается абсолютно сходящийся ряд с суммой
можно почленно складывать. В результате получается абсолютно сходящийся ряд с суммой  .
.
Теорема о произведении абсолютно сходящихся рядов. Произведение двух абсолютно сходящихся рядов  и
и 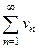 с суммами
с суммами 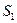 и
и  есть абсолютно сходящийся ряд
есть абсолютно сходящийся ряд 
 ,
,
сумма которого равна  .
.
Для условно сходящихся рядов соответствующие теоремы не имеют места.
Теорема Римана. Перестановкой членов условно сходящегося ряда можно получить сходящийся ряд с суммой, равной любому наперед заданному числу, или расходящийся ряд.
Переставляя члены условно сходящегося ряда, можно добиться того, что сумма ряда изменится. Например, ряд  условно сходится по признаку Лейбница. Переставим члены ряда так, что после одного положительного члена будут находиться два отрицательных. Получим ряд
условно сходится по признаку Лейбница. Переставим члены ряда так, что после одного положительного члена будут находиться два отрицательных. Получим ряд


 .
.
Сумма числового ряда изменилась, поэтому действия над рядами нельзя производить, не убедившись в их абсолютной сходимости.
Пример 4. Исследовать сходимость ряда  .
.
Решение. Составим ряд из абсолютных величин: 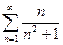 . Применим второй признак сравнения:
. Применим второй признак сравнения:  . Гармонический ряд
. Гармонический ряд  расходится, поэтому по второму признаку сравнения расходится ряд
расходится, поэтому по второму признаку сравнения расходится ряд 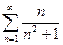 , следовательно ряд
, следовательно ряд  не является абсолютно сходящимся. Применим признак Лейбница. Так как
не является абсолютно сходящимся. Применим признак Лейбница. Так как  , то выполнено первое условие признака Лейбница. Поскольку
, то выполнено первое условие признака Лейбница. Поскольку  , имеем
, имеем  , т.е. выполнено второе условие. Ряд сходится условно.
, т.е. выполнено второе условие. Ряд сходится условно.
Пример 5. Исследовать сходимость ряда  .
.
Решение. Общий член ряда  , поэтому
, поэтому  . Следовательно, не выполнено необходимое условие сходимости ряда. Ряд расходится.
. Следовательно, не выполнено необходимое условие сходимости ряда. Ряд расходится.
Пример 6. Исследовать сходимость ряда  .
.
Решение. Составим ряд из абсолютных величин:
 . Этот ряд есть бесконечно
. Этот ряд есть бесконечно
убывающая геометрическая прогрессия и, следовательно, сходится. Значит, и данный ряд сходится, причем абсолютно.
Пример 7. Исследовать сходимость ряда  .
.
Решение. Составим ряд из абсолютных величин:  . Так как при
. Так как при 
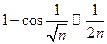 , то по второму признаку сравнения ряд из модулей расходится, следовательно, ряд
, то по второму признаку сравнения ряд из модулей расходится, следовательно, ряд  не является абсолютно сходящимся. Проверим выполнение условий признака Лейбница: 1) неравенство
не является абсолютно сходящимся. Проверим выполнение условий признака Лейбница: 1) неравенство 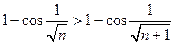 выполняется для любого
выполняется для любого  2)
2)  . Следовательно, по признаку Лейбница исходный ряд сходится условно.
. Следовательно, по признаку Лейбница исходный ряд сходится условно.
Пример 8. Вычислить сумму ряда  с точностью
с точностью 
Решение. Данный ряд знакочередующийся и сходящийся (абсолютно). Члены ряда убывают по абсолютной величине:  , при любом
, при любом  . Следовательно, справедливо неравенство
. Следовательно, справедливо неравенство  . Если
. Если  , то и
, то и 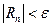 . Поэтому решая неравенство
. Поэтому решая неравенство 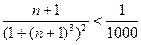 , находим количество членов ряда, которое необходимо взять для вычисления суммы с заданной точностью
, находим количество членов ряда, которое необходимо взять для вычисления суммы с заданной точностью 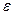 . Получаем
. Получаем  , т.е. достаточно взять первые три члена ряда. Вычисляем.
, т.е. достаточно взять первые три члена ряда. Вычисляем. 

.
Пример 9. Исследовать сходимость ряда
 .
.
Составим ряд из абсолютных величин:
 .
.
Этот ряд есть бесконечно убывающая геометрическая прогрессия и, следовательно, сходится. Значит, и данный ряд сходится, причем абсолютно.
,
 2015-10-22
2015-10-22 11031
11031







