1. Определить, какой является тройка 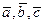 (правой или левой), если
(правой или левой), если
1) 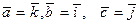 ; 2)
; 2) 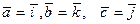
3) 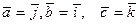 .
.
2. Векторы 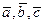 , образующие правую тройку, взаимно перпендикулярны. Зная, что
, образующие правую тройку, взаимно перпендикулярны. Зная, что 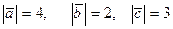 , вычислить
, вычислить 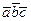 .
.
3. Даны векторы 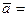 { 1; -1; 3},
{ 1; -1; 3}, 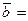 {-2; 2; 1},
{-2; 2; 1}, 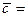 { 3; -2; 5}. Вычислить
{ 3; -2; 5}. Вычислить 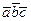 .
.
4. Установить компланарны ли векторы 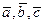 , если
, если
1) 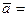 { 2; 3; -1},
{ 2; 3; -1}, 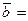 {1; -1; 3},
{1; -1; 3}, 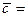 { 1; 9; 11};
{ 1; 9; 11};
2) 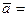 {3; -2; 1},
{3; -2; 1}, 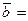 {2; 1; 2},
{2; 1; 2}, 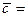 { 3; -1; -2};
{ 3; -1; -2};
3) 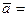 {2; -1; 2},
{2; -1; 2}, 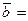 {1; 2; -3},
{1; 2; -3}, 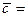 { 3; -4; 7}.
{ 3; -4; 7}.
5. Доказать, что точки A (1; 2; -1), B (0; 1; 5), C (-1; 2; 1), D (2; 1; 3) лежат в одной плоскости.
6. Вычислить объем параллелепипеда, построенного на векторах 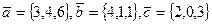 .
.
7. Вычислить объем тетраэдра, вершины которого находятся в точках A (5, 2, 2), B (-8, -2, 5), C (6, 3, 0), D (9, 3,2).
8. Вычислить объем тетраэдра, вершины которого находятся в точках A (2; -1; 1), B (5; 5; 4), C (3; 2; -1),
D (4; 1; 3).
9. Даны вершины тетраэдра A (2; 3; 1), B (4; 1; -2), C (6; 3; 7), D (-5; -4; 8). Найти длину его высоты, опущенной из вершины D.
10. Объем тетраэдра v = 5, три его вершины находятся в точках A (2; 1; -1), B (3; 0; 1), C (2; -1; 3). Найти координаты четвертой вершины D, если известно, что она лежит на оси Оу.
Ответы: 1. 1) Правая; 2) левая; 3) левая. 2. 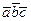 = 24.
= 24.
3. 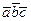 = 0,5. 4. 1)Компланарны; 2) не компланарны; 3) компланарны. 6. 43. 7. 0,5. 8. 3. 9. 11. 10.
= 0,5. 4. 1)Компланарны; 2) не компланарны; 3) компланарны. 6. 43. 7. 0,5. 8. 3. 9. 11. 10. 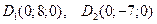
11.Заданы четыре точки:
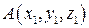 ,
,  ,
, 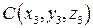 ,
, 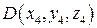 .
.
1) Проверить, что эти точки будут вершинами некоторой пирамиды и найти объем этой пирамиды.
2) Найти проекцию вектора 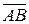 на направление вектора
на направление вектора 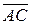 .
.
3) Найти угол 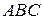 .
.
4) Найти площадь грани 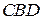 .
.
5) Найти векторное произведение и скалярное произведение векторов 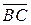 и
и 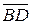 .
.
Если точки заданы координатами:
1. 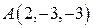
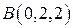
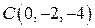
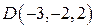
 2015-10-22
2015-10-22 1430
1430






