Пусть 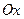 ,
, 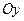 ,
, 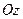 ‑ три взаимно перпендикулярные оси в трёхмерном пространстве (оси координат), исходящие из общей точки
‑ три взаимно перпендикулярные оси в трёхмерном пространстве (оси координат), исходящие из общей точки 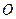 (начало координат), образуют правую тройку (т.е. для наблюдателя, находящегося по направлению оси
(начало координат), образуют правую тройку (т.е. для наблюдателя, находящегося по направлению оси 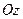 , кратчайший поворот оси
, кратчайший поворот оси 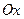 к оси
к оси 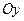 происходит против часовой стрелки).
происходит против часовой стрелки).
Для каждой точки 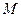 пространства существует её радиус-вектор
пространства существует её радиус-вектор 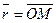 .
.
Определение 1. Под декартовыми прямоугольными координатами 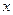 ,
, 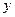 ,
, 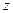 точки
точки 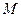 понимаются проекции её радиус вектора
понимаются проекции её радиус вектора 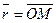 на соответствующие оси координат, т.е.
на соответствующие оси координат, т.е. 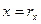 ,
, 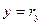 ,
, 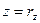 . Точка
. Точка 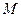 с координатами
с координатами 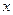 ,
, 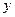 ,
, 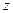 обозначается
обозначается 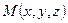 , где
, где 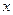 ‑ абсцисса,
‑ абсцисса, 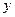 ‑ ордината,
‑ ордината, 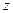 ‑ аппликата.
‑ аппликата.
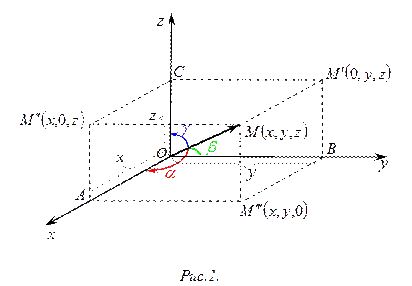
Для нахождения координат, через точку 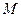 проводятся три плоскости перпендикулярные осям
проводятся три плоскости перпендикулярные осям 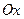 ,
, 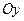 ,
, 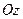 . Тогда на этих осях получатся направленные отрезки (рис.1)
. Тогда на этих осях получатся направленные отрезки (рис.1)
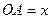 ,
, 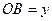 ,
, 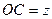 ,
,
численно равные координатам точки 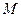 .
.
Радиус-вектор 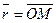 ‑ диагональ параллепипеда, поэтому
‑ диагональ параллепипеда, поэтому
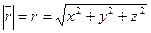 .
.
Если обозначить 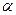 ,
, 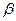 ,
, 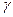 (
(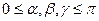 ) углы, образованные радиус-вектором
) углы, образованные радиус-вектором 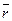 с координатными осями
с координатными осями 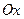 ,
, 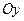 ,
, 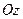 , то
, то
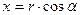 ,
, 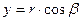 ,
, 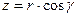 .
.
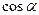 ,
, 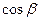 ,
, 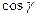 называются направляющими косинусами радиус-вектора
называются направляющими косинусами радиус-вектора 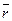 .
.
Так как
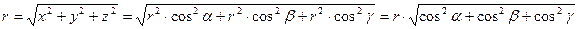 ,
,
то 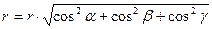 и
и 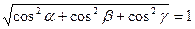 . Следовательно,
. Следовательно,
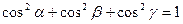
сумма квадратов направляющих косинусов радиус-вектора точки пространства равна 1.
Определение 2. Если в пространстве 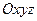 задан вектор
задан вектор  , то проекции этого вектора на оси координат
, то проекции этого вектора на оси координат
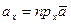 ,
, 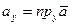 ,
, 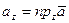
называются координатами вектора  . При этом вектор записывается так:
. При этом вектор записывается так: 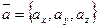 .
.
Так как вектор  свободный, то его можно рассматривать как радиус-вектор точки
свободный, то его можно рассматривать как радиус-вектор точки 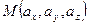 . Отсюда получаем длину вектора
. Отсюда получаем длину вектора
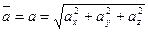 ,
,
т.е. модуль вектора равен корню квадратному из суммы квадратов его координат.
Направляющие косинусы вектора  определяются из уравнений
определяются из уравнений
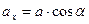 ,
, 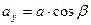 ,
, 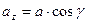 ,
,
т.е.
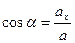 ,
, 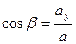 ,
, 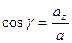 .
.
Пример. Найти длину и направление вектора 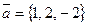 .
.
Решение. 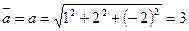 ,
, 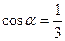 ,
, 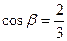 ,
, 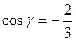 .
.
 2015-06-28
2015-06-28 9720
9720
