2015-10-22
2074
Поверхностью второго порядка называют совокупность точек пространства, координаты которых x, y, z удовлетворяют уравнению
Коэффициенты 
могут принимать любые действительные значения и удовлетворяют условию 
.
Для определения вида поверхности второго порядка необходимо ее уравнение привести к виду, не содержащему произведений координат. Этого можно достичь соответствующим выбором системы координат.
называют квадратичной формой. Матрицу
,
где 
, называют матрицей квадратичной формы. Вектор 
, удовлетворяющий условию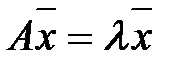 
называют собственным вектором матрицы А, 
- собственным значением.
Каждая матрица квадратичной формы имеет три взаимно ортогональных собственных вектора. Если единичные векторы собственных векторов матрицы А принять за единичные векторы новой системы координат, то в выражении квадратичной формы коэффициенты при произведениях обратятся в ноль и форма примет вид:
.
Присоединяя к ней линейную часть общего уравнения поверхности второго порядка и выделяя полные квадраты, получим каноническое уравнение поверхности второго порядка.
|
|
|
Преобразование уравнения линии второго порядка проводят аналогично. Рассмотрим пример.
Пример 24. Привести к каноническому виду уравнение кривой второго порядка и сделать чертёж:
17x2 +8y2 +12xy +10x – 8y + 5 = 0.
Решение.
Составим матрицу квадратичной формы:
.
Найдем собственные векторы линейного преобразования из условия:
.
Полученная система однородная. Она имеет ненулевые решения, если определитель системы равен нулю:
,
Отсюда находим: 
.
Найдём собственные векторы.
При 
получим систему уравнений:
Полагая 
, найдём 
.
Получим первый собственный вектор 
.
При 
получим систему уравнений:
Откуда 
, 
.
Получим второй собственный вектор 
.
Найдём орты собственных векторов.
, 
Запишем матрицу преобразования:
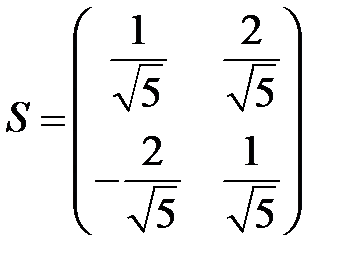
Формулы линейного преобразования примут вид:
или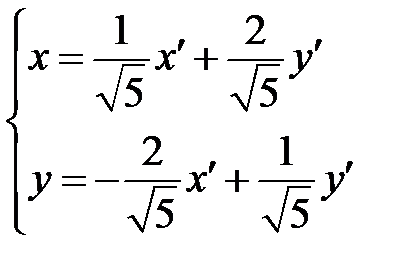 
.
Подставим значения 
и 
в уравнение кривой:
или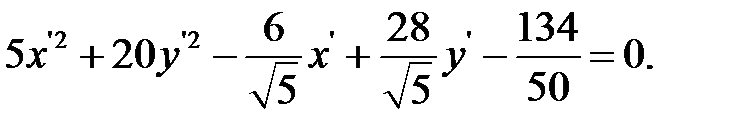 
Выделяя полные квадраты, получим:
.
Введём новые координаты:
Совершив параллельный перенос осей координат и разделив на 5 обе части уравнения, получим каноническое уравнение:
Это уравнение описывает эллипс, полуоси которого 
.
Построим эллипс по полученному уравнению.
| у |
| у / |
| у // |
| х |
| х / |
| х // |
|
|
|
|
|
|
|
| О |
