Кривые второго порядка

Кривой второго порядка называется линия на плоскости, описываемая уравнением второй степени относительно переменных x и y, т.е.

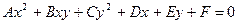, (2.4.1)

где 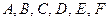- некоторые константы.

В зависимости от значений коэффициентов графиками кривых второго порядка являются окружности, эллипсы, гиперболы и параболы.

Каноническое уравнение окружности с центром в точке 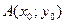и радиусом R, имеет вид

(2.4.2)

Любое уравнение вида (2.4.1) со значениями коэффициентов 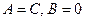определяет на плоскости окружность и может быть представлено в виде (2.4.2).

Характеристическое свойство окружности: все точки окружности удалены от одной, называемой центром, на одно и то же расстояние, равное радиусу R.

Пример 2.4.1. Найти координаты центра и радиус окружности

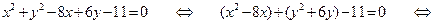Решение: выделим в уравнении полные квадраты при переменных

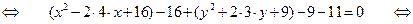
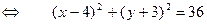
- получили уравнение вида (2.4.2). Следовательно, координаты центра окружности 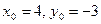, а радиус Δ

Каноническое уравнение эллипса имеет вид:

(2.4.3)

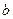Любое уравнение вида (2.4.1) со значениями коэффициентов определяет на плоскости эллипс и может быть представлено в виде (2.4.3). Числа и называются, соответственно, большой и малой полуосями эллипса. Точки 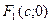и , где , называются фокусами эллипса. Точки 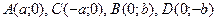называются вершинами эллипса.

Характеристическое свойство эллипса: для любой точки эллипса сумма расстояний этой точки до фокусов есть величина постоянная, равная 2а.

Пример 2.4.2. Составить уравнение прямой, проходящей через правый фокус и нижнюю вершину эллипса .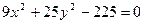

Решение: представим уравнение 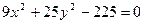в виде (2.4.3)

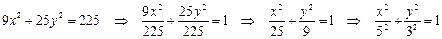
Следовательно, 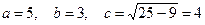- параметры эллипса, точка 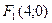- правый фокус, а - нижняя вершина эллипса.

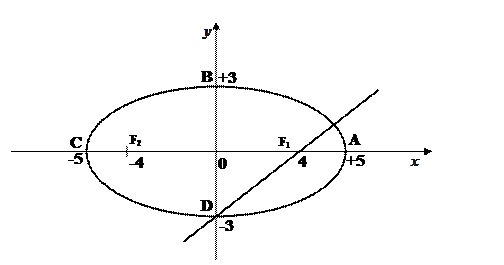
Рис. 7. Эллипс 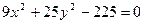и прямая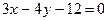

Искомая прямая проходит через точки и 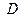, поэтому ее уравнение можно найти по формуле (2.1.3)

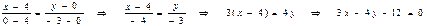Таким образом, прямая, проходящая через правый фокус и нижнюю вершину эллипса 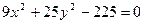имеет уравнение 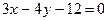Δ.

Каноническое уравнение гиперболы имеет вид:

(2.4.4)

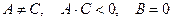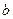Любое уравнение вида (2.4.1) со значениями коэффициентов определяет на плоскости гиперболу и может быть представлено в виде (2.4.4). Числа и называются, соответственно, действительной и мнимой полуосями гиперболы. Точки 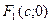и , где 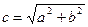, называются фокусами гиперболы. Точки 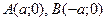называются вершинами гиперболы. Прямые, заданные уравнениями 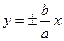, являются асимптотами гиперболы.

Характеристическое свойство гиперболы: для любой точки гиперболы разность расстояний этой точки до фокусов по абсолютной величине есть величина постоянная, равная 2а.

Гипербола с уравнением 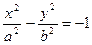или 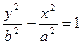называется сопряженной к гиперболе с уравнением (2.4.4), имеет тот же осевой прямоугольник и асимптоты, но пересекает ось OY в точках 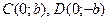и фокусы лежат на оси OY.

Пример 2.4.3. Построить гиперболу и найти расстояние от вершин гиперболы до асимптот.

Решение:

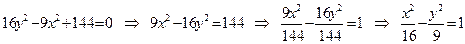преобразуем уравнение к каноническому виду (2.4.4)

Следовательно, .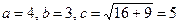

Построим осевой прямоугольник гиперболы – прямоугольник, стороны которого задаются уравнениями 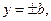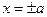. Вершины гиперболы – точки 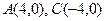. Фокусы гиперболы - 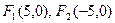. Диагонали прямоугольника – прямые - асимптоты гиперболы.

Рис. 8. Гипербола

Так как гипербола симметрична относительно осей OX и OY, то все расстояния от вершин до асимптот совпадают между собой и равны по формуле (2.1.11) расстоянию от точки 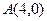до прямо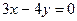й (или 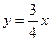- уравнение одной из асимптот гиперболы)

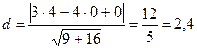(ед.) Δ

Каноническое уравнение параболы, проходящей через начало координат и симметричной относительно оси OX, имеет вид:

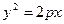(2.4.5)

Число называется параметром параболы, вершиной является начало координат, фокус находится в точке , директриса параболы имеет уравнение 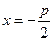. Любое уравнение вида (2.4.1) со значениями коэффициентов 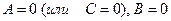определяет на плоскости параболу и может быть представлено в виде (2.4.5).

Характеристическое свойство параболы: для любой точки параболы расстояния от этой точки до фокуса и до директрисы равны между собой.

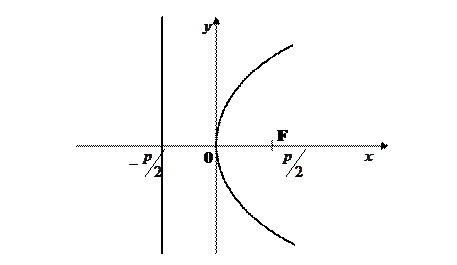
Рис. 9. Парабола

Уравнение вида 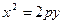(2.4.6) описывает параболу, симметричную относительно оси OY.

Пример 2.4.4. Составить каноническое уравнение параболы, вершина которой лежит в начале координат и которая проходит через точку , OX – ось симметрии.

Решение: если парабола симметрична относительно оси OX и ее вершина - в начале координат, то каноническим уравнением является уравнение вида (2.4.5)

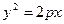
Так как точка принадлежит параболе, то ее координаты удовлетворяют уравнению параболы. Значит,

параметр параболы.

Каноническое уравнение параболы

Задача 1. Определить соответствие между кривыми и уравнениями линий:

1) гипербола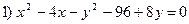

2) эллипс

3) окружность

4) прямая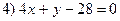

5) парабола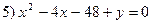

Задача 2. Определить соответствие уравнений парабол и координат их вершин:

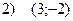
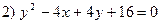
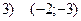
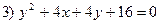
Задача 3. Построить эллипс с уравнением 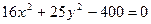и прямую, проходящую через верхнюю вершину и левый фокус эллипса.

Задача 4. Построить гиперболу, одним из фокусов которой является точка с координатами (24;0), а уравнение одной из асимптот 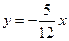. Найти расстояние от фокусов гиперболы до асимптот.