Двойственность в задачах линейного программирования. Анализ полученных оптимальных решений

С каждой задачей линейного программирования тесно связа­на другая линейная задача, называемая двойственной; первона­чальная задача называется исходной, или прямой. Связь исходной и двойственной задач заключается, в частности, в том, что решение одной из них может быть получено непосредственно из решения другой.

Переменные двойственной задачи у_i называются объективно обусловленными оценками, или двойственными оценками, или «ценами» ресурсов, или теневыми ценами.

Каждая из задач двойственной пары фактически является са­мостоятельной задачей линейного программирования и может быть решена независимо от другой.

Двойственная задача по отношению к исходной составляется согласно следующим правилам:

1) целевая функция исходной задачи формулируется на макси­мум, а целевая функция двойственной задачи - на минимум, при этом в задаче на максимум все неравенства в функцио­нальных ограничениях имеют вид (≤), в задаче на минимум - ­вид (≥);

2) матрица А, составленная из коэффициентов при неизвестных в системе ограничений исходной задачи, и аналогичная мат­рица А^Т в двойственной задаче получаются друг из друга транс­понированием;

3) число переменных в двойственной задаче равно числу функци­ональных ограничений исходной задачи, а число ограничений в системе двойственной задачи - числу переменных в исходной;

4) коэффициентами при неизвестных в целевой функции двой­ственной задачи являются свободные члены в системе ограни­чений исходной задачи, а правыми частями в ограничениях двойственной задачи - коэффициенты при неизвестных в це­левой функции исходной;

5) каждому ограничению одной задачи соответствует переменная другой задачи, номер переменной совпадает с номером огра­ничения. При этом ограничению, записанному в виде не­равенства ≤, соответствует переменная, связанная условием неотрицательности. Если функциональное ограничение исход­ной задачи является равенством, то соответствующая переменная двойственной задачи может принимать как положительные, таки отрицательные значения.

Модель исходной (прямой) задачи в общем виде может быть записана следующим образом: ; ; ,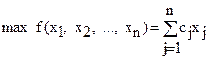

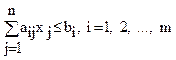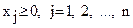а модель двойственной задачи -­ ; ; .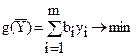

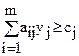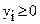Для взаимно двойственных за­дач имеет место один из взаимоисключающих случаев:

1. В прямой и двойственной задачах имеются оптимальные решения, при этом значения целевых функций на оптимальных решениях совпадают f *(Х) = g*(Y);

2. В прямой задаче допустимое множество не пусто, а целевая функция на этом множестве не ограничена сверху. При этом у двойственной задачи будет пустое допустимое множество;

3. В двойственной задаче допустимое множество не пусто, а целе­вая функция на этом множестве не ограничена снизу. При этом у прямой задачи допустимое множество оказывается пустым;

4. Обе из рассматриваемых задач имеют пустые допустимые мно­жества.

Пусть Х = (x₁, x₂,..., x_n) - допустимое решение прямой задачи, а Y = (y₁, y₂,..., y_m) - допустимое решение двойственной задачи. Для того чтобы они были оптимальными решениями соот­ветственно прямой и двойственной задач, необходимо и достаточ­но, чтобы выполнялись следующие соотношения:

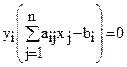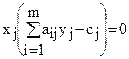(1.4) (1.5)

Условия (1.4) и (1.5) позволяют, зная оптимальное решение одной из взаимно двойственных задач, найти оптимальное реше­ние другой задачи.

Рассмотрим еще одну теорему, выводы которой будут исполь­зованы в дальнейшем.

Теорема об оценках. Значения переменных y_i в оптимальном реше­нии двойственной задачи представляют собой оценки влияния сво­бодных членов b_i системы ограничений (неравенств) прямой задачи на величину .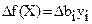

Решая ЗЛП симплекс-методом, мы одновременно решаем двой­ственную ЗЛП. Переменные двойственной задачи y_i называют объективно обусловленными оценками.

Рассмотрим экономическую интерпретацию двойственной за­дачи на примере задачи о коврах.

Пример Используя постановку задачи о коврах, выполнить следующие задания.

1. Сформулировать экономико-математическую модель задачи о коврах на максимум общей стоимости продукции, используя данные табл. 1.

2. Используя Поиск решения, найти такой план выпуска продукции, при котором общая стоимость продукции будет макси­мальной.

3. Сформулировать экономико-математическую модель двой­ственной задачи к задаче о коврах.

4. Найти оптимальный план двойственной задачи, используя теоремы двойственности, пояснить равенство нулю X₁ и X₄.

5. Используя протоколы Поиска решения, выполнить анализ по­лученного оптимального решения исходной задачи.

6. Определить, как изменится общая стоимость и план выпуска продукции при увеличении запаса ресурса труб на 12 ед.

Решение

1. Сформулируем экономико-математическую модель задачи.

Обозначим через X₁, Х₂, X₃, Х₄ число ковров каждого типа. Целевая функция имеет вид: f (Х) = 3X₁ + 4Х₂ + 3X₃ + Х₄ → max, а ограничения по ресурсам:

7Х₁ + 2X₂ + 2X₃ + 6Х₄ ≤ 80,

5Х₁ + 8Х₂ + 4Х₃ + 3Х₄ ≤ 480,

2Х₁ + 4Х₂ + Х_З + 8Х₄ ≤130,

Х₁, Х₂, Х_3, X₄ ≥ 0.

2. Поиск оптимального плана выпуска.

Решение задачи выполним с помощью надстройки Excel Поиск решения. Технология решения задачи была подробно рассмотрена в задаче о костюмах. В нашей задаче оптимальные значения вектора Х = (Х₁, Х₂, Х₃, Х₄) будут помещены в ячейках В3:Е3, оптимальное значение целевой функции - в ячейке F4.

Введем исходные данные. Сначала опишем целевую функцию с помощью функции - СУММПРОИ3В (рис. 19). А потом введем данные для левых частей ограничений. В Поиске решения введем направление целевой функции, адреса искомых переменных, до­бавим ограничения. На экране появится диалоговое окно Поиск решения с введенными условиями (рис. 20).

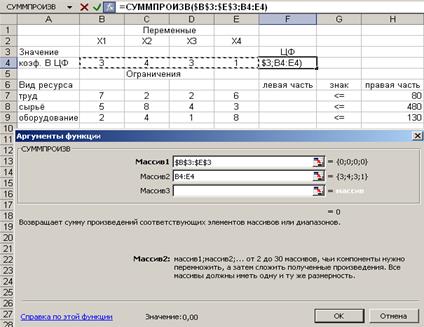
Рис. 19. Вводится функция для вычисления целевой функции

После ввода параметров для решения ЗЛП следует нажать кнопку Выполнить. На экране появится сообщение, что решение найдено (рис. 21).

Полученное решение означает, что максимальный доход 150 тыс. руб. фабрика может получить при выпуске 30 ковров второго вида и 10 ковров третьего вида. При этом ресурсы «труд» и «оборудование» будут использованы полностью, а из 480 кг пряжи (ресурс «сырье») будет использовано 280 кг.

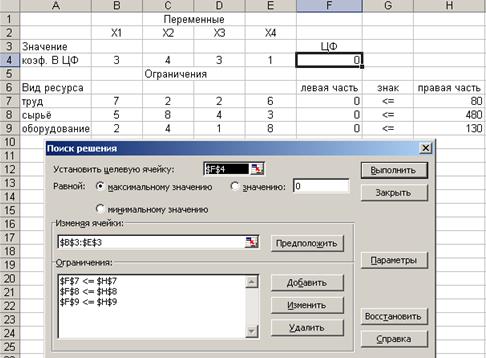
Рис. 20. Введены все условия задачи

Создание отчета по результатам поиска решения. Excel позволяет представить результаты поиска решения в форме отчета (табл. 4). Существует три типа таких отчетов:

§ Результаты (Answer). В отчет включаются исходные и конечные значения целевой и изменяемых ячеек, дополнительные све­дения об ограничениях.

§ Устойчивость (Sensitivity). Отчет, содержащий сведения о чувстви­тельности решения к малым изменениям в изменяемых ячей­ках или в формулах ограничений.

§ Пределы (Limits). Помимо исходных и конечных значений из­меняемых и целевой ячеек, в отчет включаются верхние и ниж­ние границы значений, которые могут принимать влияющие ячейки при соблюдении ограничений.

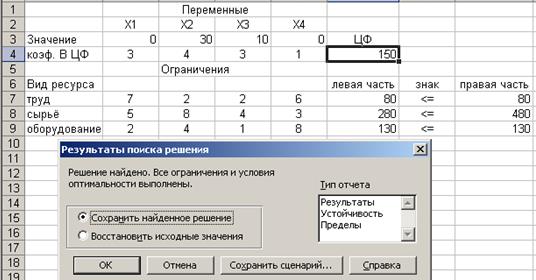
Рис. 21. Решение найдено