Операции алгебры логики обладают свойствами, аналогичными операциям сложения и умножения обычной алгебры. Имеют место следующие законы:
- сочетательный (ассоциативный)
x 1(x 2 x 3) = (x 1 x 2) x 3; x 1 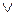 (x 2
(x 2 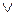 x 3) = (x 1
x 3) = (x 1 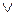 x 2)
x 2) 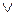 x 3
x 3
- переместительный (коммутативный)
x 1 x 2 = x 2 x 1; x 1 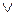 x 2 = x 2
x 2 = x 2 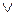 x 1
x 1
- распределительный (дистрибутивный)
x 1(x 2 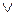 x 3) = x 1 x 2
x 3) = x 1 x 2 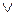 x 1 x 3
x 1 x 3
x 1 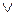 (x 2 x 3) = (x 1
(x 2 x 3) = (x 1 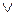 x 2)(x 1
x 2)(x 1 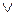 x 3).
x 3).
На основании этих законов можно выносить переменные за скобки, переставлять местами и т.д., как и в обычной алгебре. Но только для алгебры логики действует закон двойственности (правило де Моргана):
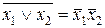
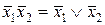 .
.
Законы двойственности обобщены К. Шенноном для любых булевых функций (ФАЛ):
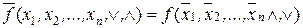 .
.
Такая запись обозначает тот факт, что отрицание над записью всей функции приводит к отрицанию значения переменных и знаков, их соединяющих, т.е. дизъюнкция (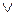 ) заменяется знаком конъюнкции (
) заменяется знаком конъюнкции (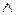 ), и наоборот.
), и наоборот.
Пример:
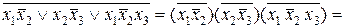
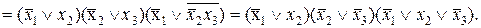 (*)
(*)
Заметим, что в первоначальную запись функции (*) можно значительно упростить. Действительно, вынесем за скобки 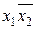 , тогда получим:
, тогда получим:
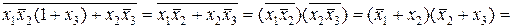
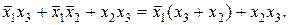
Из законов алгебры логики следуют следующие очевидные соотношения:
|
|
|
1 + x = 1, 1· x = x, x + 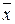 = 1. 0· x = 0, x·x = x, x ·
= 1. 0· x = 0, x·x = x, x · 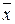 = 0, 0 + x = x, x + x = x.
= 0, 0 + x = x, x + x = x.
Использование этих законов позволяет упрощать исходную запись ФАЛ. Вернемся к анализу ФАЛ, представленной в таблице 5.
В первой исходной записи ФАЛ, полученной по таблице 5, в каждом логическом произведении переменных (конъюнкция) присутствовали все переменные из набора x 1 x 2 x 3 x 4, а сами конъюнкции соединены символом логического сложения (дизъюнкции). Такая форма записи ФАЛ называется совершенной дизъюнктивной нормальной формой (СДНФ).
Если не все переменные из набора x 1 x 2 x 3 x 4 представлены в каждой из конъюнкций, то такая форма по прежнему остается нормальной дизъюнктивной формой, но она не относится к классу совершенных. Дизъюнктивных нормальных форм представления одной и той же ФАЛ может быть много, но совершенная ДНФ (СДНФ) одна единственная. Кроме СДНФ существует так называемая конъюнктивная нормальная форма, которая также может быть совершенной (СКНФ) и не совершенной, т.е. просто КНФ. КНФ представляет собой алгебраическое выражение в виде стольких конъюнктивных членов, представляющих собой дизъюнкции всех переменных, при скольких наборах значений переменных функция равна 0. Если в наборе значение переменной равно 1, в дизъюнкцию входит инверсия этой переменной. Например, для табл. 5 получим:
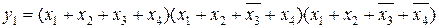
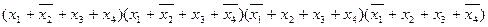
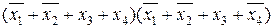 .
.
Анализ СДНФ и СКНФ показывает неэкономичность записи ФАЛ. Используя свойства ФАЛ можно преобразовать выражения за счет так называемой операции склеивания, т.е.
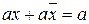 , т.к.
, т.к. 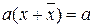 .
.
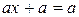 ,
,
где a – любая ФАЛ.
Упрощение записи СДНФ за счет операции склеивания называется минимизацией ФАЛ. Существует большое число алгоритмов минимизации ФАЛ, из которых наиболее наглядным и простым является метод карт Карно.
|
|
|
Карта Карно представляет собой булево пространство в виде матрицы клеток, в которых отображаются конституенты СДНФ. Конституента – это набор переменных, соединенных знаком конъюнкции. Если функция при этом наборе переменных равна 1, то в клетку матрицы записывается 1. Черточками над клетками булева пространства помечаются строки и столбцы (по горизонтали и по вертикали), в которых обозначенная переменная примет значение 1.
В табл. 11 представлена ФАЛ, для которой СДНФ имеет вид:
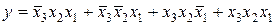 .
.
В таблице 11 значение х 1 = 1 распространяется на столбцы 2 и 3, считая справа налево, а значение х 2 = 1 – на столбцы 1 и 2. Аналогично черточка х 3 = 3 относится к нижней строке таблицы (матрицы).
В таблице 11 введены уровни симметрии по столбцам и строкам. Нулевой (0) уровень делит матрицу пополам, единичные уровни (1) делят каждую область строк или столбцов еще раз пополам. Как видно, по строкам только один нулевой (0) уровень симметрии, а по столбцам их 2.
Таблица 11
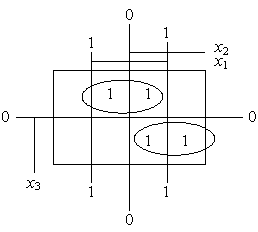
Для минимизации все клетки, содержащие 1, объединяются в замкнутые области с числом клеток 2, 4, 8… (в зависимости от числа переменных в ФАЛ). Области могут пересекаться, и одни и те же клетки могут входить в разные области. «Соседними» являются не только клетки, расположенные рядом по горизонтали и вертикали, но и клетки, находящиеся на противоположных границах карты. При охвате клеток замкнутыми областями следует стремиться к минимальному числу областей.
Для табл. 11 получим:
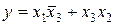 .
.
Одним из вариантов карты Карно является представление кодирования булева пространства кодом Грея, в котором при переходе от клетки к клетке как по вертикали, так и по горизонтали меняется значение только одной переменной.
Такое представление хорошо воспринимается визуально благодаря симметрии по осям. В данном случае это оси «0–0» и «1–1». Эта симметрия позволяет легче находить области склеивания конституент, для которых значения какой-либо переменной xi не влияет на значение ФАЛ. Речь идет о «ручной» минимизации с использованием визуального восприятия, что эффективно при n ≤ 6.
Действительно, для верхней области, охватывающей две 1 при 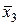 , видно, что значение x 2 несущественно, т.к. ФАЛ равна 1 как при x 2, так и при
, видно, что значение x 2 несущественно, т.к. ФАЛ равна 1 как при x 2, так и при 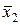 , но обе 1 в булевом пространстве при
, но обе 1 в булевом пространстве при 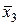 лежат в области x 1. Аналогично для значения x3 не существенно значение x 1, но обе 1 соответствуют x 2.
лежат в области x 1. Аналогично для значения x3 не существенно значение x 1, но обе 1 соответствуют x 2.
Для столь простого примера нельзя сделать четкий вывод в пользу того или иного способа кодирования булева пространства, но при числе переменных, равном 4, 6 и более, преимущества кода Грея будут очевидны при визуальном методе минимизации ФАЛ.
Минимизация ФАЛ базируется на использовании свойств карт Карно. Наборы значений переменных для соседних клеток карты Карно отличаются лишь одной переменной. При переходе из клетки в соседнюю всегда изменяется значение лишь одной переменной от своего прямого значения к его инверсии и обратно.
Соседними между собой являются также крайние левые клетки карты с крайними правыми и крайние верхние клетки карты с крайними нижними (как если бы карты были свернуты в цилиндры по вертикали и горизонтали).
Таким образом, все клетки, отличающиеся значением только одной переменной, являются соседними, несмотря на то, что иногда они расположены не рядом. Это свойство карты является очень важным для определения минимальных алгебраических выражений функций.
Совершенная дизъюнктивная нормальная форма СДНФ логической функции, изображенной в виде карты Карно, определяется следующим образом:
- для каждой клетки, в которой функция имеет значение 1, записывается конъюнкция всех входных переменных (прямых или инверсных);
|
|
|
- составляется дизъюнкция этих конъюнкций, которая и представляет собой СДНФ данной функции.
Для логической функции, заданной на карте Карно, можно записать несколько алгебраических выражений различной сложности в дизъюнктивной или конъюнктивной форме. При этом целесообразно пользоваться следующими рекомендациями:
1. Все единицы (при записи функции в дизъюнктивной форме) и все нули (при записи функции в конъюнктивной форме) должны быть заключены в прямоугольные контуры. Единичные контуры могут объединять несколько единиц, но не должны содержать внутри себя нулей. Нулевые контуры могут объединять несколько нулей, но не должны содержать внутри себя единиц. Одноименные контуры могут накладываться друг на друга, т.е. одна и та же единица (или нуль) может входить в несколько единичных (нулевых) контуров.
2. Площадь любого контура должна быть симметричной относительно границ переменных, пересекаемых данным контуром. Другими словами, число клеток в контуре должно быть равно 2 n, где п = 0, 1, 2, 3, 4,..., т.е. число клеток выражается числами 1, 2, 4, 8, 16, 32, ….
3. Во избежание получения лишних контуров, все клетки которых вошли уже в другие контуры, построение следует начинать с тех единиц или нулей, которые могут войти в один-единственный контур.
4. В контуры можно объединять только соседние клетки, содержащие единицы или нули. Соблюдение этого правила особенно необходимо проверять при числе переменных, большем четырех, когда соседние клетки могут быть расположены не рядом и поэтому контуры могут претерпевать видимый разрыв.
5. Каждой единичной клетке соответствует конъюнкция входных переменных, определяющих данную клетку. Каждой нулевой клетке соответствует дизъюнкция инверсий входных переменных, определяющих данную клетку.
6. В контуре, объединяющем две клетки, одна из переменных меняет свое значение. Поэтому выражение для контура из двух клеток не зависит от этой переменной, а представляется всеми остальными переменными. Это правило относится и к контурам, охватывающим число клеток более двух, и имеет такую формулировку: выражения, соответствующие контурам, не содержат тех переменных, чьи границы пересекаются площадью, ограниченной данным контуром.
|
|
|
7. Выражение логической функции может быть записано по соответствующей ей карте Карно в дизъюнктивной или конъюнктивной формах. Дизъюнктивная форма составляется в виде дизъюнкции конъюнкций, соответствующих единичным контурам, выделенным на карте для определения функции. Конъюнктивная форма составляется в виде конъюнкции дизъюнкций, соответствующих нулевым контурам.
8. Для контуров, охватывающих различное количество клеток, получаются выражения различной сложности. Поэтому для данной логической функции можно записать по карте Карно несколько отличающихся по сложности алгебраических выражений. Наиболее сложное выражение соответствует случаю, когда каждой клетке соответствует свой контур. Это выражение представляет собой набор СДНФ и СКНФ данной функции. С увеличением размеров контуров алгебраическое выражение упрощается. Самое простое выражение функции получается при образовании наибольших контуров. На этом свойстве основывается метод минимизации логических функций с помощью карт Карно.
Рассмотрим пример ФАЛ для шести переменных (табл. 12). Все области 1, объединенные двойными линиями, представляют один интервал ФАЛ, для которого по горизонтали очевидна независимость от x 1 и x 3, а по вертикали от x 4 и x 6, т.е. весь интервал соответствует 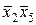 . Верхняя область, объединенная сплошным овалом в одну линию по горизонтали, соответствует x 2 x 3, а по вертикали
. Верхняя область, объединенная сплошным овалом в одну линию по горизонтали, соответствует x 2 x 3, а по вертикали 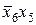 , т.е.
, т.е. 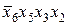 , а нижняя соответствует
, а нижняя соответствует 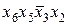 , тогда получим:
, тогда получим:
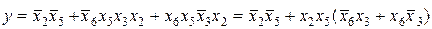 .
.
Последняя запись в скобках для х 3 и х 6 как уже говорилось называется функцией (обозначим Ζ) суммы по модулю 2 и обозначаются символом  . Другое название функции Ζ – функция неравнозначности, т.к. она принимает значение 1 только при различных значениях переменных.
. Другое название функции Ζ – функция неравнозначности, т.к. она принимает значение 1 только при различных значениях переменных.
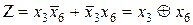 .
.
Таблица 12

Заметим, что обратная ей функция 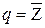 имеет вид:
имеет вид:
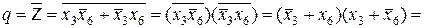
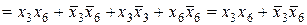 .
.
Эта функция называется функцией тождественности, т.к. она принимает значение 1 только при одинаковых (тождественных «0» и «1») значениях переменных
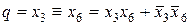 .
.
Тогда выражение для y можно записать в виде
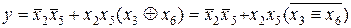 .
.
Существуют функции, значение которых неопределенно на некоторых наборах входных переменных, т.е. некая комбинация, например 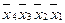 , не может быть реализована. Практических примеров таких булевых функций много, особенно для реальных технологических процессов. Все такие комбинации переменных также наносятся на карту Карно и отмечаются символом, отличающимся от символа «0» или «1», с целью получения минимальной формы булевых функций Такие булевы функции называются не полностью определенными*.
, не может быть реализована. Практических примеров таких булевых функций много, особенно для реальных технологических процессов. Все такие комбинации переменных также наносятся на карту Карно и отмечаются символом, отличающимся от символа «0» или «1», с целью получения минимальной формы булевых функций Такие булевы функции называются не полностью определенными*.
КОМБИНАЦИОННЫЙ ПРЕОБРАЗОВАТЕЛЬ ИНФОРМАЦИИ
РАСПРЕДЕЛЕННЫХ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ
ОБРАБОТКИ СИГНАЛОВ
Распределенные микропроцессорные системы с явно выделенными логическими преобразователями информации (ЛПИ) позволяют обеспечить параллельность и высокую скорость обработки информации, что очень важно в задачах реального времени, быстрых алгоритмах обработки сигналов и др.
Организация ЛПИ в виде параллельно организованной структуры позволяет вычислять наиболее сложные операции (типа умножения) за ограниченное число тактов. Метод построения ЛПИ для реализации операции умножения при числе разрядов п ≤8 сводится к представлению произведения С = А∙Вв виде разности квадратов:
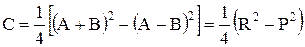 , (2)
, (2)
где R = A + B, P = A – B.
Логическое выражение для R2 и Р2находится методом прямого считывания из ПЗУ или через комбинационные схемы с использованием минимизации булевых функций по картам Карно для каждого qi разряда квадратора. Квадратор – это устройство, определяющее величину x в степени 2, если x задано в виде кода.
Такой традиционный путь синтеза возможен для небольших значений п (n ≤ 8), но уже при n > 6 этот путь синтеза затруднен, т.к. требует умения проводить процедуру минимизации по картам Карно большой размерности, а число таких карт равно 2∙ n.
Поэтому более предпочтительным может оказаться аналитический способ получения минимальных выражений для соответствующих разрядов преобразователей. Этот способ учитывает особенности операции возведения в квадрат на основе применения вертикальной процедуры обработки информации [29].
Рассмотрим первый способ минимизации на примере синтеза структуры четырехразрядного квадратора (синтез на основе карт Карно).
В этом случае расположим все восемь карт Карно для четырех входных переменных в соответствии с весом выходной переменной yi (табл. 13). При возведении в квадрат число выходных переменных необходимо взять в 2 раза больше. Для каждой карты по горизонтали закодированы все комбинации х1х0: 00, 01, 11, 10, а по вертикали – х3х2. Для кодирования применен код Грея.
Заполним эти карты в соответствии со значениями чисел у = х2 при
изменении х в диапазоне от 0 до 15. Тогда получим следующие комбинации расположения единиц и нулей на картах Карно (табл. 13).
Проводя минимизацию по картам Карно, получим минимальные выражения для yi:
y 0 = x 0; y 1 = 0; y 2 = 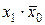 ; y 3 =
; y 3 = 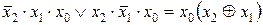 ;
;
у 4 = 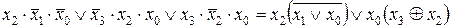 ; (3)
; (3)
у 5 = 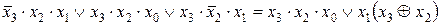 ;
;
y 6 = 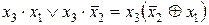 ;
;
y 7 = x 3∙ x 2.
Таблица 13
Представление чисел у = х 2на картах Карно
| yi | y 7 | y 6 | y 5 | y 4 | y 3 | y 2 | y 1 | y 0 | ||||||||||||||||||||||||
Теперь с учетом выражений (3) получим структуру комбинационного квадратора (рис. 11), которая в виде единого блока изображена на рис. 12.
Функциональные и логические преобразователи
дискретной автоматики
Проектирование устройств дискретной автоматики начинается с выбора соответствующей системной модели. Модель позволяет классифицировать и формализовать структурное описание системы автоматики, найти адекватные средства математического описания процессов, осуществить постановку задач оптимизации.
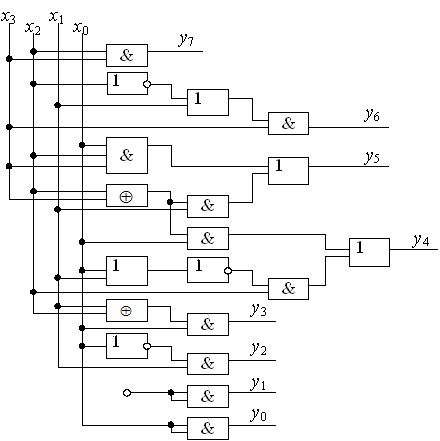
Рис. 11. Структура квадратора
|
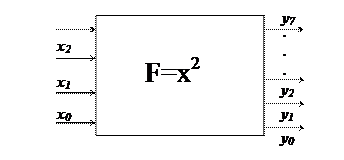
Рис. 12. Квадратор
Если на наборе xn, xn- 1, …, x 2, x 1 двоичных переменных задана система булевых функций y 1, y 2, …, ym, которую обобщенно обозначим символом F, то она может быть реализована неким устройством (рис. 13), которое называется «черным ящиком», так как структурная организация его не известна. Поскольку xi, yj 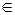 {0,1}, то реализация такого устройства называется комбинационной схемой, т.к. для конкретного значения набора xi,
{0,1}, то реализация такого устройства называется комбинационной схемой, т.к. для конкретного значения набора xi, 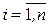 (который называется комбинацией) определено значение yj,
(который называется комбинацией) определено значение yj, 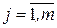 .
.

Рис. 13
Простейшей реализацией комбинационной схемы F является постоянное запоминающее устройство (ПЗУ), тогда y1, y2, …, ym – значения на выходных «клеммах» ПЗУ или коды соответствия x 1, x 2, x 3, …, xn 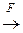 y 1, y 2, …, ym, которые «записаны» в числовой блок ПЗУ как константы, где x 1, x 2, x 3, …, xn – адрес ПЗУ.
y 1, y 2, …, ym, которые «записаны» в числовой блок ПЗУ как константы, где x 1, x 2, x 3, …, xn – адрес ПЗУ.
Модель «черного ящика» является простейшей системообразующей моделью для представления устройств, т.к. она позволяет на основе изучения объекта управления найти это соответствие, т.е. формализованное правило преобразования { x }→{ y }.
В задачах проектирования и определения структурной организации автомата модель «черного ящика» оказывается полезной в двух случаях:
1) Функция системы управления действительно может быть выражена автоматом с одним внутренним состоянием. Тогда другие структурные модели не требуются, и детальное проектирование связано лишь с определением параметрических характеристик (объем памяти, число каскадов и др.) структуры ВПИ.
2) Функция системы более сложна, не может быть сведена к функции автомата с одним состоянием, но анализ по модели «черного ящика» позволяет полностью уточнить все входы и выходы, уяснить требуемую форму представления входных и выходных сигналов, разрядность представления сигналов по входам и выходам.
После этого требуется перейти к анализу и проектированию структурной организации системы на основе более детальных моделей.
Комбинационные схемы (КС) называют автоматом с одним состоянием, т.к. достаточно подать переменные на вход, и на выходе с задержкой, определяемой временем прохождения сигналов через последовательность элементов И, ИЛИ, НЕ, появляются значения выходных переменных. В реальных системах КС не используются независимо. Входные переменные записываются на входной регистр памяти, а выходные на выходной. Запись и считывание результата с регистров производится с помощью импульсов синхронизации, которые формирует в заданной последовательности автомат управления. Одиночные импульсы синхронизации, поданные на исполнение того или иного действия (запись, считывание) называются микрооперациями (МО), а автомат – микропрограммным автоматом (МПА).
 2015-10-22
2015-10-22 2328
2328
