Речь идет не о суммировании двух одноразрядных чисел, а о суммировании именно двух одноразрядных переменных, т.к. при суммировании двух чисел необходимо учитывать значение возможного переноса из предыдущего разряда. При суммировании двух переменных «входного» переноса нет. Поэтому такую схему в вычислительной технике называют полусумматор.
Составим комбинационную таблицу 8 для суммы (S) и переноса (P) – как функций двух двоичных переменных а, b.
Таблица 8
Проанализируем столбец S. Как видно, значение S равно «1» в двух случаях: когда комбинация ab равна 01 (т.е.  ) и 10 (т.е. ) и 10 (т.е.  ). ).
| Входы | Выходы | |
| а | b | S | Р |
Определим функции S и Ркак логические дизъюнкции (операция «ИЛИ») конъюнкций (операция «И») а и b, при которых выходная функция равна 1; при этом, если переменная равна 0, то в конъюнкции эта переменная берется с отрицанием. Тогда получим булевы функции для Sи P: S = 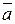 b + a
b + a  , P = ab.
, P = ab.
Несмотря на кажущуюся простоту, непосредственная реализация S и Р на элементах И, ИЛИ, НЕ (рис. 5) неэкономична.
Докажем что ( )(a+b) =
)(a+b) =  . Для этого воспользуемся теоремой Моргана:
. Для этого воспользуемся теоремой Моргана:  =
= 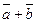 . Тогда (
. Тогда ( )(a+b) = (
)(a+b) = (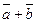 )(a+b) =
)(a+b) =  = =
= =  , т.к.
, т.к.  , как и
, как и  , равны «0». По формуле получим новую схему (рис. 6)*.
, равны «0». По формуле получим новую схему (рис. 6)*.
Как видно, вместо трех «И», одной схемы «ИЛИ» и двух схем «НЕ» в такой реализации использовано: схема «И», одна «И–НЕ» и одна схема «ИЛИ». Этот простейший пример убеждает в необходимости минимизации булевых функций. В дальнейшем при рассмотрении систем из более сложных булевых функций эффективность минимизации будет еще более очевидной.
 2015-10-22
2015-10-22 328
328








