Для заданной балки двутаврового сечения ( = 210 МПа, Е = 2 х 105 МПа) и нагрузок требуется;
= 210 МПа, Е = 2 х 105 МПа) и нагрузок требуется;
1. Построить эпюры поперечных сил и изгибающих моментов;
2. Определить нормальные и касательные напряжения в сечениях с наибольшим моментом и поперечной силой на расстоянии h/4 от нейтральной оси;
3. Определить прогиб конца балки точки В.
При построении эпюр Q и М необходимо соблюдать правило знаков. Положительное направление сил показано на схеме.

РЕШЕНИЕ.
1. Определяем опорные реакции







2. Методом сечений определяем ординаты поперечной силы в характерных сечениях. Для этого балку разбиваем на два участка. Границы участков - места изменения нагрузки. Построение эпюры начинаем с правого свободного конца балки.
Максимум изгибавшего момента находится в сечении, где поперечная сила равна нулю. Положение этого сечения определяем из условия:


3. Методом сечений определяем изгибающие моменты в характерных сечениях и строим эпюру моментов. Экстремум в т. х = 2 м.

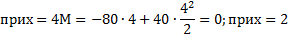

Наиболее нагруженным сечением в балке является сечение А у заделки, где Мmax = 120 кН м, Qmах = - 80 кН.
4. Из условий прочности по нормальным напряжениям определяем требуемый момент сопротивления сечения.

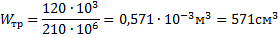
По сортаменту ГОСТ 8509-72 принимаем двутавр № 33.


Максимальные напряжения в опасном сечении будут равны


5. Определяем нормальное напряжение в точке Е сечения на расстоянии h/4 = 8,25 см от нейтральной оси (рис. 4.9.).



Для определения касательного напряжения в точке Е вычислим статический момент отсеченной выше точки Е площади относительно центральной оси Х.
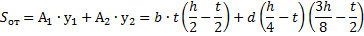


6. Определяем прогиб балки в точке В, используя универсальное уравнение прогибов
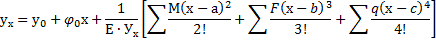
Для заданной консольной балки граничные условия будут: угол поворота сечения А  ; прогиб сечения А
; прогиб сечения А 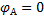
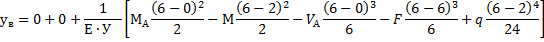

 2015-10-22
2015-10-22 7057
7057
