Вопрос 18.Определение перемещений при изгибе. Интеграл Мора. Метод Верещагина

Прогиб – линейная деформация, смещение центра тяжести поперечного сечения.

Интеграл Мора позволяет определять прогибы и углы поворота заданного сечения балки, используя интегральное исчисление.

- перемещение сечения К под действием Р, где M_xp-изгибающий момент в произвольном сечении, _х - единичный момент в том же сечении под действием единичной силы или единичного момента (если ищется угол поворота), EI_x– жёсткость сечения балки при изгибе.

Правило Верещагина. Используется, когда жёсткость при изгибе постоянна вдоль длины. Эпюра изгибающих моментов должна быть линейной. Максимальный прогиб называется стрелой.

Следует иметь в виду, что способы «перемножения» эпюр применимы только при наличии двух условий:

1.Изгибная жесткость балки на рассматриваемом участке должна быть постоянной (EI=Const),

2.Одна из двух эпюр моментов на этом участке (грузовая или единичная) должна быть обязательно линейной. При этом обе эпюры не должны в пределах данного участка иметь перелома.

Δ_кр= 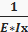* ω_p * _k^c - грузовое перемещение

ω_p – площадь грузовой эпюры.

_k^c - ордината в единичном эпюре, соответствует центру тяжести грузовой.

При постоянной жесткости по длине балки EI_z для определения прогиба энергетическим методом необходимо вычислять интеграл вида:

.

Допустим, что эпюры изгибающих моментов аналитически выражаются функциями М_z=f₁(х), М^’_z´ = f₂(х), причем одна из них, например, f₁(х) произвольная, а другая f₂(х) линейная функция и может быть записана в виде f₂(х) = kх+b. Пусть графики этих функций имеют вид представленный на рис. 3.86.

Рисунок 3.86

В соответствии с принятыми обозначениями можно записать:

Первый интеграл представляет собой статический момент относительно оси x площади эпюры ограниченной кривой M_z, т.е.

, где

ω – площадь, ограниченная кривой M_z,

х_c - координата центра тяжести фигуры ограниченной кривой M_z относительно оси х.

Второй интеграл представляет собой площадь, ограниченную кривой M_z, которую обозначили ω.

Следовательно:

Итак,

Таким образом, искомый интеграл равен произведению площади эпюры M_z на расположенную под ее центром тяжести ординату эпюры М_z´. Важно отметить, что вычисление перемещения способом Верещагина возможно только в том случае, когда, во-первых, эпюры M_z и М_z ´ на рассматриваемом участке не имеют изломов, во-вторых, одна из эпюр описывается линейной зависимостью и именно по ней определяется ордината под центром тяжести другой эпюры y_c. Поэтому при вычислении способом Верещагина интеграл Мора по всей длине балки надо заменить суммой интегралов по участкам, в пределах которых эпюра моментов от единичной нагрузки не имеет изломов. Тогда перемещение сечения балки δ:

Таким образом, для вычисления прогибов по способу Верещагина необходимо:

1) построить эпюру изгибающих моментов от заданных нагрузок M_z (основная эпюра);

2) снять внешнюю нагрузку (но сохранить опоры) и приложить в том сечении, в котором определяется перемещение (угол поворота) единичную силу (единичный момент) в направлении искомого.перемещения (угла поворота);

3) построить эпюру изгибающих моментов от единичной нагрузки М_z ´(единичная эпюра);

4) разбить эпюры на участки, в пределах которых отсутствуют изломы эпюр, и для каждого участка вычислить площадь криволинейной эпюры ω_i и ординаты эпюр ограниченных линейной функцией под центрами тяжести криволинейных эпюр у_ci.

5) составить произведения ω_i у_ci и просуммировать:

Встречающиеся на практике эпюры изгибающих моментов разбивают на простейшие фигуры: прямоугольник, треугольник и параболический треугольник.

Площади этих фигур и координаты центров тяжести приведены в таблице

Вид эпюры Mz	Площадь w	Координата центра тяжести xc
	ab / 2	a / 3
	ab / 3	a/ 4
	ab / 4	a / 5
	2ab / 3	a / 2
	2ab / 3	5a / 8