1. Допустимое множество задачи ЛП либо пусто, либо является выпуклым многогранником в Rn (как пересечение полупространств, описываемых неравенствами (2)-(3)). Оно может быть как ограниченным, так и неограниченным; в любом случае это замкнутый многогранник.
2. Если допустимое множество не пусто, а целевая функция ограничена сверху (для задачи максимизации, а для задачи минимизации - ограничена снизу) на этом множестве, то задача ЛП имеет оптимальное решение.
3. Оптимальные решения задачи ЛП (если они существуют) всегда находятся на границе допустимого множества. Точнее, если существует единственное оптимальное решение, то им является какая-либо вершина многогранника допустимых решений; если две или несколько вершин являются оптимальными решениями, то любая их выпуклая комбинация также является оптимальным решением (т.е. существует бесконечное множество точек максимума или минимума).
Методами решения задач ЛП являются:
1. графический метод (в случае двух переменных),
2. симплекс-метод или его разновидности (в общем случае).
|
|
|


Симплекс-метод.
Пример:
Max Z=18X1+20X2+32X3

Max z=18X1+20X2+32X3+0*X4+0X5+0X6
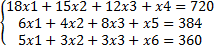
| БП | СБ | Ао | X1 | X2 | X3 | X4 | X5 | X6 |
| X4 | ||||||||
| X5 | ||||||||
| X6 | ||||||||
| -18 | -20 | -32 | 0 |
Приведем задачу к каноническому виду и занесем в симплексную таблицу. Если все оценки неотрицательны, то начальный опорный план оптимален. Если существует хоть одна отрицательная оценка, план не оптимален и при определенных условиях его можно улучшить.
Среди отрицательных оценок находим максимальное по модулю. Столбец этой оценки называется разрешающим. Если задача решается на минимум, то разрешающим является столбец с максимальной оценкой среди положительных. Переменную, соответствующую разрешающему столбцу, следует ввести в базис. Для определения переменной, выводимой из базиса, находят отношение bi/Ai(720/12, 384/8, 360/3 для этого случая, x3). Среди этих отношений находят минимальное. Оно и содержит переменную, которую выводим из базиса. Данная строка называется разрешающей. Элемент, стоящий на пересечении разрешающего столбца и разрешающей строки называется разрешающим элементом. Для завершения шага составляется новая таблица по следующим правилам:
1)Все элементы разрешающего столбца в новой таблице равны нулю за исключением разрешающего элемента-он всегда равняется единице.
2)Элементы разрешающей строки в новой таблице равны соответствующим элементам старой таблицы, деленным на разрешающий элемент.
3)Чтобы получить все остальные элементы данной таблицы, нужно применить правило прямоугольника, т.е. произведение главной диагонали минус произведение побочной диагонали деленное на разрешающий элемент. Главной является диагональ, содержащая разрешающий элемент.
|
|
|
| БП | СБ | Ао | X1 | X2 | X5 | X4 | X5 | X6 |
| X4 | ||||||||
| X3 | 0.75 | 0.5 | 0.125 | |||||
| X6 | ||||||||
((720*8)-(384*12))/8=144
(360*8)-(384*3)/12=216
 2015-10-22
2015-10-22 393
393







