Мінімізація функцій методом Квайна — Мак-Класкі

Метод мінімізації Квайна — Мак-Класкі також реалізує перехід від ДДНФ до мінімальної ДНФ з використовуванням операцій склеювання та поглинання. Він був запропонований В. Квайном, а потім удосконалений Мак-Класкі.

Алгоритм Квайна складається з таких кроків:

1. Записати ДДНФ заданої функції.

2. Виконати всі можливі операції неповного диз'юнктивного склеювання. Результуюча формула є диз'юнкцією всіх мож­ливих імплікант даної функції.

3. Виконати всі можливі операції диз'юнктивного погли­нання. Результуюча формула є скороченою ДНФ даної функції.

4. Скласти імплікантну таблицю і знайти диз'юнктивне ядро.

5. Спростити імплікантну таблицю за допомогою видалення рядків, що відповідають імплікантам диз'юнктивного ядра, і стовпців, що відповідають тим конституентам одиниці, які покриваються імплікантами ядра.

6. Знайти всі тупикові ДНФ даної функції.

7. Знайти мінімальну ДНФ.

Якщо при мінімізації деякої функції виходить, що спро­щена імплікантна таблиця порожня, то тупикова ДНФ цієї функції є мінімальною і складається тільки з імплікант ди­з'юнктивного ядра. Якщо ж спрощена імплікантна таблиця не порожня, то в кожній тупиковій ДНФ функції, крім імплікант ядра, присутні і деякі прості імпліканти, що не входять до диз'юнктивного ядра. Набір даних імплікант визначає різниці між тупиковими ДНФ.

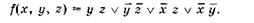Зробивши попарне порівняння всіх елементарних ко-н'юнкцій, що входять у дану формулу, приходимо до виснов­ку, що одержати інші елементарні кон'юнкції за допомогою операції склеювання в даній формулі неможливо. Таким чином, одержано диз'юнкцію всіх можливих імплікант даної функції:

Одержана формула є скороченою ДНФ даної функції. Складемо імплікантну таблицю (таблиця 4.33). її рядки за­даються простими імплікантами, а стовпці — конституентами одиниці функції. Зірочкою відзначається кожна клітка табли­ці, для якої імпліканта з рядка є власною частиною консти-туенти із стовпця.

Знайдемо диз'юнктивне ядро. До нього входить кожна проста імпліканта, яка є єдиною у покритті будь-якої консти-туенти одиниці. В імплікантній таблиці по одному знаку «*» містять стовпці, що відповідають конституентам одиниці хуг і хуг, напроти простих імплікант у z і у z. Ці прості імпліканти складають диз'юнктивне ядро. Складемо спрощену імплікант­ну таблицю. Для цього з імплікантної таблиці викреслюємо рядки, що відповідають імплікантам диз'юнктивного ядра, і стовпці, що відповідають конституентам одиниці, які покриті імплікантами ядра (таблиця 4.34).

В даному випадку імпліканти ядра покривають всі кон-ституенти одиниці, крім однієї, тому спрощена імплікантна таблиця має такий вигляд (таблиця 4.35):

Із спрощеної імплікантної таблиці знаходимо, що тупикові ДНФ даної функції, крім диз'юнктивного ядра, включають або імпліканту х z, або х у. Таким чином, одержуємо дві тупикові ДНФ для даної функції:

Вказані ДНФ містять по 6 символів змінних, а також од­накову кількість знаків операцій диз'юнкції (2) і кон'юнкції (3), тому виберемо як мінімальну ДНФ1, що містить менше знаків операцій заперечення.

В методі Квайна для функції більшого числа змінних перелічення варіантів склеювання і множини тупикових ДНФ є значною складністю. Удосконалення, що введене Мак-Класкі, спрощує запис мінімізаційної формули. Згід­но з його пропозицією конституенти одиниці записуються у вигляді двійкового коду — номери даної конституенти. Вка­заний номер відповідає інтерпретації, на якій конституен-та дорівнює одиниці. Всі останні імпліканти, що одержані в результаті застосування операцій неповного склеювання, також записуються у вигляді двійкових кодів. У позиціях коду, що відповідають реальним змінним імпліканти, помі­щається набір значень змінних, який обертає імпліканту на одиницю. В позиціях фіктивних змінних імпліканти ста­виться прочерк. Таким чином, операції склеювання і погли­нання проводяться не з самими імплікантами, а з їх двій­ковими кодами, що робить алгоритм простим у програмній реалізації.

Крім того, множина кодів імплікант ділиться на гру­пи за кількістю одиниць, що в них утримуються. Оскільки операції неповного склеювання застосовні до імплікант, ко­ди яких відрізняються значенням тільки в одній позиції, в склеюванні можуть брати участь тільки імпліканти, що належать до сусідніх груп, номери яких відрізняються на одиницю. Крім того, виконання операцій склеювання здійсню­ється покроково. На першому кроці здійснюються всі мож­ливі склеювання конституент одиниці, на другому кроці здійснюється склеювання на множині імплікант, що одержані на першому кроці, тощо. Ділення на групи та кроки дозво­ляє істотно скоротити кількість перевірок пар імплікант на можливість здійснення склеювання і робить алгоритм більш ефективним.

При виконанні операцій поглинання з формули видаляю­ться всі імпліканти, що не є простими. Результуюча формула зображує диз'юнкцію простих імплікант функції — її скорочену ДНФ. Імпліканти, що брали участь хоча б в одному склеюван­ні, не є простими. Отже, замість операцій поглинання можна видалити з формули всі імпліканти, що брали участь хоча б в одному склеюванні, з однаковим результатом. Тому при виконанні операцій склеювання одержані імпліканти познача­ються. Після виконання всіх можливих склеювань позначені імпліканти видаляються. Це дає той же результат, що і при виконанні операцій поглинання.

Формальний метод знаходження множини всіх тупикових ДНФ функції був запропонований С. Петриком. У цьому ме­тоді кожній з простих імплікант функції, що не входять до диз'юнктивного ядра, приписується буквене позначення. Нага­даємо, що пошук простих імплікант проводиться у спрощеній імплікантній таблиці. За допомогою цієї таблиці записується логічна формула покриття конституент одиниці простими імплікантами. Для цього для кожної конституенти одиниці складається диз'юнкція літерних позначень всіх простих ім­плікант, які її покривають. Далі записується формула, що зображує кон'юнкцію одержаних елементарних диз'юнкцій. В формулі розкриваються всі дужки, після чого вона здобуває вид диз'юнкції елементарних кон'юнкцій. Кожна елементарна кон'юнкція в одержаній формулі відповідає одній з тупикових ДНФ функції. Для побудови такої ДНФ необхідно записати імпліканти, що відповідають літерним позначенням, які вхо­дять до складу даної елементарної кон'юнкції, й імпліканти диз'юнктивного ядра функції.

Приклад. Знайти за допомогою метода Квайна — Мак-Кла-скі мінімальну ДНФ функції f(x, у, г, t), що задана такою ДДНФ:

Розв'язок. У таблиці 4.36 запишемо конституенти одиниці даної функції у вигляді двійкових кодів у другий стовпчик. У першому стовпці запишемо десяткові номери інтерпретацій.

Відповідно до методу здійснимо такі кроки:

1. Згрупуємо двійкові коди імплікант з однаковою кількістю одиниць. Назвемо число одиниць т індексом групи. Упо­рядкуємо групи у порядку зростання т.

2. Починаючи з т = 0, зробимо порівняння кожного двійко­вого коду в групі з індексом т з кожним кодом з групи з індексом т + 1. Якщо порівнювані двійкові коди різні тільки в одному розряді, то у наступний стовпчик табли­ці запишемо відповідний їм двійковий код з порожньою позначкою «-» на місці зазначеного розряду. Напроти кож­ного нового коду запишемо номери кодів двох імплікант, що брали участь у порівнянні, і у наступному стовпчику ці імпліканти позначимо знаком «V», оскільки вони не є простими імплікантами. Всі коди, які залишилися непо-значеними знаком «V», відповідають простим імплікантам, тому позначимо їх знаком «X».

3. Якщо серед знов одержаних імплікант є однакові, то з них для подальшого використання залишаємо тільки одну.

4. Повторюємо кроки 1-3 доти, доки існує можливість одер­жувати нові коди імплікант.

Результат виконання описаних кроків наведено у таб­лиці 4.37. Спочатку заповнюємо три стовпця нульового циклу: т (десятковий індекс групи), двійковий код імшпкан-ти, номер імпліканти. Імпліканти ділимо на групи за зна­ченням т.

Потім здійснимо порівняння першої імпліканти з групи т = 0 (імпліканта 0000) з першою імплікантою з групи т = 1 (імпліканта 0001). Вони відрізняються тільки в одному розря­ді, тому робимо їх склеювання та одержуємо нову імпліканту з кодом 000-. Записуємо даний код у стовпчик коду імпліканти циклу 1, а напроти імплікант 0000 і 0001 ставимо позначки «V», оскільки вони не є простими. їх номери вказуємо поряд з кодом 000-. Потім порівнюємо імпліканту 0000 з другою імп­лікантою з групи т = 1 — імплікантою 0010 тощо.

Коли порівняння всіх кодів імплікант стовпця «цикл 0» завершено, аналізуємо стовпчик виду імпліканти. Напроти всіх імплікант ставимо позначення «V», оскільки в циклі 0 кожна імпліканта припускає склеювання і не є простою. Далі розділяємо на групи m = 0, т = 1 і т = 2 коди імплікант циклу 1. Потім попарно порівнюємо ці імпліканти й одержуємо стовпчик коду імплікант «цикл 2». Коди, що містять знаки «-», можуть утворювати нові імпліканти, тільки якщо вони містять знаки «-» в одних і тих же розрядах. Закінчивши порівнян­ня, виділяємо прості імпліканти у стовпці «вид» «циклу 1», які не мають позначки «V», і позначаємо їх позначкою «X». У стовпці «код» «циклу 2» є однакові імпліканти, тому довіль­но викреслюємо один з однакових рядків, щоб кожна імплікан-та зустрічалася тільки один раз. Порівнюючи коди імплікант у «циклі 2», приходимо до висновку, що методом склеювання з них неможливо одержати нові імпліканти. Всі коди циклу 2 відповідають простим імплікантам, отже, побудову таблиці за­вершено.

Для знаходження тупикових ДНФ побудуємо імплікант-ну таблицю, в рядках якої розташовуємо двійкові коди, що відповідають простим імплікантам, а в стовпцях — коди, що відповідають конституентам одиниці. Якщо двійковий код рядку є частиною коду стовпця (позиції із знаком «-» не порівнюються), то у відповідну клітку таблиці записуємо знак «*» (таблиця 4.38).

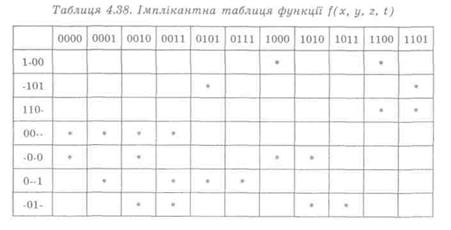
Відзначимо стовпці таблиці, які містять по одному зна­ку «*». Відповідні їм прості імпліканти є диз'юнктивни­ми ядрами. Викреслюємо рядки таблиці, що відповідають ядрам, і стовпці, покриті ядрами, як зображено у табли­ці 4.39.

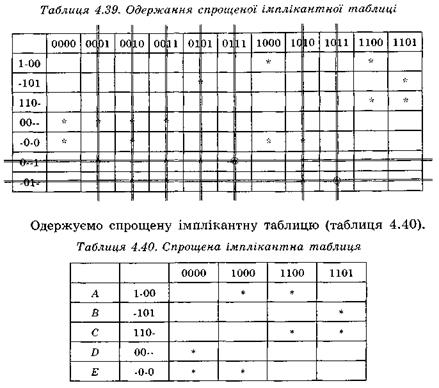
Тепер знайдемо всі тупикові ДНФ функції f(x, у, z, t) і оберемо з них мінімальну. Згідно з методом Петрика кожній з імплікант таблиці приписуємо літерне позначення і записуємо формулу покриття конституент одиниці простими імпліканта-ми. Конституента одиниці з кодом 0000 може бути покрита імплікантою D або імплікантою Е, тобто диз'юнкції: D v E. Конституента одиниці з кодом 1000 може бути покрита імплі­кантою А або імплікантою Е: A v E. Аналогічно 1100 може бути покрита A v С, а 1101 — диз'юнкцією В v С. Таким чином, покриття конституент одиниці спрощеної імплікантної таблиці функції f(x, у, z, t) простими імплікантами можна записати у вигляді формули покриття:

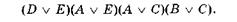
Якщо в цій формулі розкрити дужки, то отримаємо сим­вольне зображення всіх можливих наборів простих імплікант для тупикових ДНФ, що не включає диз'юнктивні ядра:

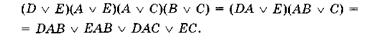
В одержаній формулі кожна кон'юнкція буквених позна­чень відповідає набору імплікант у деякій тупиковій ДНФ, до якої обов'язково входять також диз'юнктивні ядра. Для того щоб одержати мінімальну ДНФ, необхідно вибрати набір з мінімальною кількістю імплікант (у даному прикладі це EC) і додати імпліканти ядра (0--1, -01-). Одержуємо мінімальну ДНФ вихідної функції f:

Таким чином, за допомогою метода Квайна — Мак-Класкі одержана мінімальна ДНФ функції f(x, у, г, t), яка містить всього лише 4 елементарні кон'юнкції замість 11 конституент одиниці ДДНФ.

Недолік методу мінімізації булевих функцій Квайна — Мак-Класкі полягає у необхідності записувати ДДНФ функції, яка вже при семи змінних може містити більше ста конституент одиниці. Наступний метод дозволяє здійснювати диз'юнкти­вну мінімізацію, використовуючи як вихідну довільну ДНФ функції.