Устойчивость за пределом пропорциональности. Расчет сжатых стержней на устойчивость

1 Предположим, что сжимающая сила вызывает в стержне напряжения превышающие предел пропорциональности, но меньшие, чем предельное напряжение (для пластичного материала за предельное напряжение принимают предел текучести, для хрупкого – предел прочности). Для определения критической силы, при данном условии, используется…

1)коэффициент понижения основного допускаемого напряжения

2)формула Ясинского

3)метод последовательности приближений

4)формула Эйлера

2 Формула Ясинского применима, если…

1)напряжение в сжатом стержне превышает предел пропорциональности, но меньше предельного напряжения для данного материала

2)напряжение в сжатом стержне меньше предела пропорциональности

3)напряжение в сжатом стержне меньше допускаемого напряжения

4)гибкость сжатого стержня больше предельной гибкости

3 Формула Ясинского применима, если…

1)гибкость стержня больше предельной гибкости

2)критическое напряжение больше предела пропорциональности

3)гибкость стержня равна нулю

4)гибкость для сжатого стержня лежит в пределах , где предельная гибкость; гибкость стержня, в котором напряжение достигает предельного напряжения для данного материала.

4 Формулу Ясинского можно использовать при расчете…

1)на жесткость

2)на прочность

3)сжатых стержней на устойчивость, когда напряжение в стержне превышает предел пропорциональности, но меньше значения предельного напряжения для данного материала

4)сжатых стержней на устойчивость до предела пропорциональности

5 Стержень с шарнирно опертыми концами длиной м сжат силой F. Зависимость критического напряжения от гибкости для стали Ст. 3 приведена на рисунке. Поперечное сечение стержня представляет собой двутавр №22, радиусы инерции которого 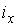= 9,13 см, = 2,27 см. Критическое напряжение для стержня равно…

1) 240 МПа

2) 220 МПа

3) 100 МПа

4) 200 МПа

6 Стержень, защемленный одним концом, длиной м сжат силой F. Зависимость критического напряжения от гибкости для стали Ст. 3 приведена на рисунке. Поперечное сечение стержня представляет собой двутавр №20, радиусы инерции которого 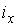= 8,28 см, = 2,07 см. Критическое напряжение для стержня равно…

1) 240 МПа

2) 162 МПа

3) 213 МПа

4) 200 МПа

7 Стержень длиной м, шарнирно опертый одним концом и жестко защемленный другим, сжат силой F. Зависимость критического напряжения от гибкости для стали Ст. 3 приведена на рисунке. Поперечное сечение стержня представляет собой двутавр №18, радиусы инерции которого 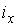= 7,42 см, = 1,88 см. Критическое напряжение для стержня равно…

1) 233 МПа

2) 240 МПа

3) 200 МПа

4) 212 МПа

8 Стержень с шарнирно опертыми концами длиной м сжат силой F. Зависимость критического напряжения от гибкости для стали Ст. 3 приведена на рисунке. Поперечное сечение стержня представляет собой швеллер №22, радиусы инерции которого 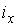= 8,89 см, = 2,37 см. Критическое напряжение для стержня равно…