Взвешенное расстояние. Алгоритм Форда-Беллмана

Пусть G=<M,R> - взвешенный граф, в котором вес каждой дуги (a,b) есть некоторое вещественное число μ(a,b). Весом маршрута a₁,…,a_n₊₁ называется число . Взвешенным расстоянием (ω-расстоянием) ρ_ω(a,b) между вершинами a и b называется минимальный из весов (a,b)- маршрутов). Маршрут с минимальным весом называется кратчайшим. Взвешенным эксцентриситетом вершины a называется величина . Взвешенной центральной вершиной называется вершина a, для которой . Взвешенный эксцентриситет центральной вершины называется взвешенным радиусом.

Пусть G=<M,R> - взвешенный граф, имеющий n вершин и матрицу весов W=(ω_ij). Предположим, что в G отсутствуют контуры с отрицательным весом, поскольку двигаясь по такому контуру достаточное число раз можно получить маршрут бесконечно малого веса.

Алгоритм Форда-Беллмана (для нахождения взвешенного расстояния от вершины a_i (источника) до всех вершин графа G):

Зададим строку 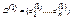, полагая 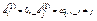. Определим строку , полагая . Нетрудно заметить, что - минимальный из весов (a_i,a_j) -маршрутов, состоящих не более чем из двух дуг.

Продолжая процесс, на шаге s определим строку , полагая . Искомая строка ω-расстояний получается при s=n-1: . Алгоритм можно завершить на шаге k, если D⁽^k⁾=D⁽^k⁺¹⁾.