Пусть G=<M,R> - граф. Последовательность a1,u1,a2,u2,…,un,an+1, где  , называется маршрутом, соединяющим вершины a1 и an+1, если ui=(ai,ai+1). Число n дуг в маршруте называется его длиной.
, называется маршрутом, соединяющим вершины a1 и an+1, если ui=(ai,ai+1). Число n дуг в маршруте называется его длиной.
Пусть G – неорграф. Маршрут (a1,an+1) называется цепью, если все ребра [a1,a2],…,[an,an+1] различны, и простой цепью, если все его вершины, кроме, возможно, первой и последней, различны. Маршрут называется циклическим, если a1=an+1. Циклическая цепь называется циклом, а циклическая простая цепь – простым циклом.
Пусть G – орграф. Маршрут называется путем, если все его дуги различны. Путь называется контуром, если a1=an+1. Граф, не имеющий контура, называется бесконтурным. Вершина b называется достижимой из вершины a, если существует (a,b) – путь.
Неорграф называется связным, если любые две его несовпадающие вершины соединены маршрутом. Граф G называется связным, если соответствующий ему неорграф F(G) тоже является связным. Граф G называется сильно связным, если для каждой пары различных вершин a и b существуют (a,b)-маршрут и (b,a)-маршрут. Аналогично определяются понятия связности и сильной связности для мультиграфов.
Всякий максимальный по включению (сильно) связный подграф данного графа называется его (сильной) связной компонентой или (сильной) компонентой связности.
Теорема: Любой граф представляется в виде объединения непересекающихся связных (сильных) компонент. Разложение графа на связные (сильные) компоненты определяется однозначно.
Теорема: Если AG – матрица смежности графа G, то (i,j)-й элемент матрицы 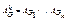 есть число (ai,aj)-маршрутов длины k.
есть число (ai,aj)-маршрутов длины k.
Следствие: 1) В графе G мощности n тогда и только тогда существует (ai,aj) -маршрут (ai≠aj), когда (i,j) -й элемент матрицы  не равен нулю.
не равен нулю.
2) В графе G мощности n тогда и только тогда существует цикл, содержащей вершину ai, когда (i,i)-й элемент матрицы  не равен нулю.
не равен нулю.
Образуем из матрицы (bij)=E+AG+AG2+…+AGn-1 матрицу C=(cij) порядка n по следующему правилу:  . Матрица С называется матрицей связности, если G – неорграф, и матрицей достижимости, если G-орграф.
. Матрица С называется матрицей связности, если G – неорграф, и матрицей достижимости, если G-орграф.
Определим матрицу контрдостижимости Q=(qij): 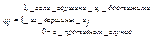 . Причем Q=CT.
. Причем Q=CT.
Рассмотрим матрицу сильных компонент S=C*Q, где операция * означает поэлементное произведение матриц С и Q: sij=cij•qij. Таким образом, матрица S является матрицей отношения эквивалентности E: выполнимо aiEaj тогда и только тогда, когда ai и aj находятся в одной сильной компоненте.
 2015-10-22
2015-10-22 1787
1787








