ax + by = r
Исходные числа a и b тоже можно представить в виде линейной комбинации a и b:

Запишем это в общем виде

Разделим a на b с остатком.

Подставим вместо a и b их представления

Приведя подобные, получим

или

Повторяя подобное деление необходимое число раз, получим

(при этом коэффициенты для следующего остатка легко находятся через коэффициенты предыдущего остатка).
Пример.
| q | ||||||||
| x | -1 | -5 | -81 | |||||
| y | -3 | -15 |
Для контроля вычислений можно проверять для каждого столбца выполнение равенства  . Например, 64·4 + 81·(-3) = 13.
. Например, 64·4 + 81·(-3) = 13.
Окончательно имеем: 64·19 + 81·(-15) = 1.
Свойства НОД
1. Если  любое положительное число, то
любое положительное число, то
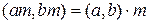 .
.
Доказательство:
Обозначим  . Имеем разложение:
. Имеем разложение:
 .
.
Умножим это равенство на  :
:

 является делителем чисел
является делителем чисел  и
и  и является линейной комбинацией этих чисел. Следовательно,
и является линейной комбинацией этих чисел. Следовательно,  является наибольшим общим делителем этих чисел:
является наибольшим общим делителем этих чисел:
 .
.
2. Если  - любой делитель
- любой делитель 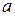 и
и  , то
, то

Согласно предыдущему:
 .
.
Деля это равенство на  , имеем:
, имеем:
 .
.
В частности,

3. Если 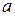 и
и  взаимно просты и
взаимно просты и  делится на
делится на  , то
, то 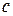 делится на
делится на  .
.
Действительно, так как 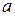 и
и  взаимно просты, то найдутся целые числа
взаимно просты, то найдутся целые числа  и
и  , такие что
, такие что
 .
.
Умножим это равенство на 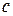 и запишем так:
и запишем так:
 . (1)
. (1)
Так как  делится на
делится на  , то левая часть равенства делится на
, то левая часть равенства делится на  . Поэтому и
. Поэтому и 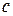 делится на
делится на  .
.
4. Если 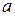 и
и  взаимно просты, то
взаимно просты, то 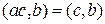 .
.
В силу равенства (1) всякий общий делитель  и
и  делит
делит 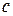 . Значит,
. Значит, 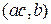 делит
делит  . Но и
. Но и  делит
делит 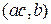 . Поэтому
. Поэтому 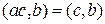 .
.
Свойства НОК.
1.Всякое кратное чисел  называется их общим кратным. Наименьшее из общих кратных называется наименьшим общим кратным чисел
называется их общим кратным. Наименьшее из общих кратных называется наименьшим общим кратным чисел  . Обозначается:
. Обозначается:  .
.
2. Свойства кратного двух чисел.
Пусть  .
.
Тогда  .
.
Пусть 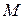 - кратное
- кратное 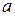 и
и  .
.
Тогда  . Но
. Но 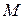 кратно и
кратно и  . Поэтому
. Поэтому
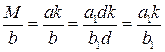 - целое число.
- целое число.
Но  , поэтому
, поэтому 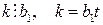 .
.
Получаем формулу:
 .
.
При любом целом 
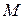 будет кратным
будет кратным 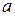 и
и  .
.
При  получаем наименьшее общее кратное:
получаем наименьшее общее кратное:
 .
.
Следовательно

Доказаны следующие теоремы.
1) Совокупность общих кратных двух чисел совпадает с совокупностью кратных наименьшего общего кратного этих чисел.
2) Это наименьшее кратное равно произведению чисел, поделенному на их наибольший общий делитель.
3. Наименьшее общее кратное трех и более чисел находится по следующему правилу.
 .
.
Если числа 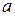 и
и  взаимно просты, то
взаимно просты, то  и
и  .
.
И вообще, если  - попарно просты, то
- попарно просты, то

 2015-10-22
2015-10-22 754
754








