Степень вхождения данного простого числа в разложение факториала

Несложно разложить на простые множители факториал натурального числа, воспользовавшись рассуждениями, наподобие только что приведённых для деления 100! на 5.

Каждое простое число p входит в разложение числа n! следующее количество раз:

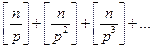
(Обоснование формулы состоит в том, что сначала рассматривают числа, кратные p, затем кратные квадрату p, затем кратные кубу p, и так далее).

Количество слагаемых не бесконечно, поскольку начиная с некоторого места они равны нулю.

Теорема Евклида о бесконечности множества простых чисел

Доказательство бесконечности множества простых чисел.

Предположим, что простых чисел конечное количество. Выпишем их все: p₁, p₂, …, p_n.

Затем перемножим все эти числа и прибавим 1. Рассмотрим число N = p₁ ∙ p₂ ∙ … ∙ p_n + 1.

Это число не может быть простым, поскольку больше любого из простых чисел.

При этом оно не может быть и составным, поскольку не делится ни на одно из простых чисел.

Получаем противоречие, которое говорит о том, что простых чисел бесконечно много.

Системы счисления

Определение.

Позиционная система счисления с основанием b – это способ записи чисел в виде .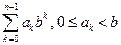

При этом a_k – цифры этого числа.

Самая распространённая система счисления – десятичная, но иногда (например, в программировании) используют и двоичную систему, и восьмеричную, и шестнадцатиричную системы счисления.

Деление часа и градуса на 60 минут и 3600 секунд осталось нам в память о шестидесятиричной системе, использовавшейся в древности.

Для перехода от недесятичной системы (например, девятиричной) к десятичной запишите выражение вида 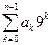, подставьте его цифры и найдите таким образом значение.

Например, 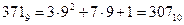, то есть число 371 в девятиричной системе равно числу 307 в десятичной системе счисления.

Обратный переход (от записи в десятичной к записи в девятеричной системе) осуществляется так. Ищем представление числа в виде 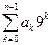, причём поиск начнём с последней цифры, которая равна остатку от деления числа на 9.

Сначала разделим число 307 на 9 с остатком, остаток равен 1. Это последняя цифра девятиричной записи числа.

(307 – 1): 9 = 34. Остаток от деления на 9 этого числа равен 7. Поэтому вторая с конца цифра равна 7.

(34 – 7): 9 = 3. Поэтому первая цифра равна 3.

Сравнение по модулю

Определение

Говорят, что a сравнимо с b по модулю c, если 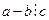. В этом случае пишут a º b (mod c), или a º b (c).

Пример

21 º 15 (mod 3).

Модульная арифметика

Определение

Кольцо остатков по данному модулю n - это множество всех остатков от деления натуральных чисел на данное число n. Это множество обозначают как Z_n.

Название «кольцо остатков» связано с тем, что множество всех остатков удовлетворяет некоторым свойствам, принятым в алгебре. Подробный список этих свойств для краткости здесь приводить не будем.

Например, составим таблицу сложения в кольце остатков по модулю 4. Складывая остатки, результат сложения заменим его остатком от деления на 4.

Например, 1 + 3 заменим 0.

+

Таблица умножения в том же кольце остатков.

х

Обратите внимание на то, что в данном кольце остатков произведение двух ненулевых чисел (2 и 2) равно нулю.