Теоретические свойства построения чертежа в инженерной графике базируются на правилах построения изображений, основанных на методе проекций. Изображение объектов трехмерного пространства на плоскости получают методом проецирования.
Проецирование – это процесс, в результате которого получают изображения, представляющие собой проекции на плоскости.
 Аппарат проецирования включает в себя изображаемые объекты – точки А, В, проецирующие лучи i и плоскость проекции п', на которой получается изображение объектов. Процесс проецирования заключается в проведении проецирующих лучей через заданные точки до встречи с плоскостью проекций. Точка пересечения проецирующего луча с плоскостью проекций и определяет проекцию этой точки. Так, проекцией точки А является точка А', т. е. [i ~ A; i ^ п' = А']. Проекцией точки В является точка В', хотя проекция точки В, лежащей в плоскости п', совпала с самой точкой. Чтобы получить проекцию какой-либо фигуры, необходимо построить проекции ее характерных точек и соединить их на чертеже соответствующими линиями.
Аппарат проецирования включает в себя изображаемые объекты – точки А, В, проецирующие лучи i и плоскость проекции п', на которой получается изображение объектов. Процесс проецирования заключается в проведении проецирующих лучей через заданные точки до встречи с плоскостью проекций. Точка пересечения проецирующего луча с плоскостью проекций и определяет проекцию этой точки. Так, проекцией точки А является точка А', т. е. [i ~ A; i ^ п' = А']. Проекцией точки В является точка В', хотя проекция точки В, лежащей в плоскости п', совпала с самой точкой. Чтобы получить проекцию какой-либо фигуры, необходимо построить проекции ее характерных точек и соединить их на чертеже соответствующими линиями.
В основу построения объекта на плоскости положен метод проекций. Проецирование – это построение объекта на плоскости при помощи п роецирующих лучей, исходящих из точки. Плоскость, на которую падают лучи – проецирующая плоскость.
| Способы проецирования | |
| I. Центральное проецирование: проецирующие лучи выходят из одной точки (центра). Размеры предмета на плоскости проекций искажаются (рис.1). | II. Параллельное проецирование: проецирующие лучи параллельны и составляют с плоскостью угол 90 градусов (прямоугольное проецирование или ортогональное рис.2) и угол отличный от 90 градусов (косоугольное проецирование рис.3). |
 |  |
 |
Аппарат проецирования включает в себя:
Пi – плоскость проекций,
S – центр проецирования,
А – объект проецирования (точка),
SA – проецирующую прямую,
Ai – проекцию точки А.
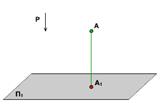 Ортогональное проецирование – это частный случай параллельного проецирования. При ортогональном проецировании проецирующие лучи перпендикулярны к плоскости проекций.
Ортогональное проецирование – это частный случай параллельного проецирования. При ортогональном проецировании проецирующие лучи перпендикулярны к плоскости проекций.
Аппарат такого проецирования состоит из одной плоскости проекций.
Чтобы получить ортогональную проекцию точки А, через неё надо провести проецирующий луч перпендикулярно к П1. Точка А1 называется ортогональной или прямоугольной проекцией точки А.
 Чтобы получить ортогональную проекцию А1В1 отрезка АВ, на плоскость П1, необходимо через точки А и В провести проецирующие прямые, перпендикулярные П1. При пересечении проецирующих прямых с плоскостью П1 получатся ортогональные проекции А1 и В1 точек А и В. Соединив ортогональные проекции А1 и В1 получим ортогональную проекцию А1В1 отрезка АВ.
Чтобы получить ортогональную проекцию А1В1 отрезка АВ, на плоскость П1, необходимо через точки А и В провести проецирующие прямые, перпендикулярные П1. При пересечении проецирующих прямых с плоскостью П1 получатся ортогональные проекции А1 и В1 точек А и В. Соединив ортогональные проекции А1 и В1 получим ортогональную проекцию А1В1 отрезка АВ.
Все свойства параллельного проецирования выполнимы и для ортогонального проецирования. Однако ортогональные проекции обладают ещё некоторыми свойствами.
Свойство ортогонального проецирования:
Для ортогонального проецирования будет справедлива теорема о проецировании прямого угла:
Теорема: Если хотя бы одна сторона прямого угла параллельна плоскости проекций, а вторая ей не перпендикулярна, то угол на эту плоскость проецируется в натуральную величину.
Доказательство:
Дан прямой угол АВС, у которого по условию прямая ВС перепендикулярна АВ и ВС || плоскости проекций П1. По построению прямая ВС к проецирующему лучу ВВ1. Следовательно, прямая ВС к плоскости b (АВхВВ1), т.к. она к двум пересекающимся прямым, лежащим в этой плоскости. По условию прямая В1С1 || ВС, поэтому тоже  к плоскости b, т. е. и прямой А1В1 этой плоскости. Следовательно, угол между прямыми А1В1 и В1С1 равен 90°, что и требовалось доказать.
к плоскости b, т. е. и прямой А1В1 этой плоскости. Следовательно, угол между прямыми А1В1 и В1С1 равен 90°, что и требовалось доказать.

Ортогональное проецирование обеспечивает простоту геометрических построений при определении ортогональных проекций точек, а так же возможность сохранять на проекциях форму и размеры проецируемой фигуры. Эти достоинства обеспечили ортогональному проецированию широкое применение в техническом черчении.
Рассмотренные методы проецирования позволяют решить прямую задачу начертательной геометрии, т.е. по оригиналу построить плоский чертёж. Полученные таким образом проекции на одну плоскость дают неполное представление о предмете, его форме и положении в пространстве, т.е. такой чертёж не обладает свойством обратимости.
Чтобы получить обратимый чертеж, т.е. чертеж, дающий полное представление о форме, размерах и положении оригинала в пространстве, однокартинный чертеж дополняют. В зависимости от дополнения существуют различные виды чертежей.
В промышленности весьма широко используются так называемые плоские детали (пластины, уголки, прокладки, решетки, лекала швейного и обувного производств и т. д.), имеющие простую или сложную конфигурацию при незначительной толщине самих деталей (рис 1). Для отображения их на чертеже достаточно построения одной проекции.

Рис. 1. Плоские детали: а — «Пластины»; б — «Уголок», в — «Прокладки»; г — «Решетки»
При прямоугольном проецировании на одну плоскость проекций деталь следует расположить таким образом, чтобы полученное изображение давало наибольшую информацию о ее форме (рис. 2).

Рис. 2. Расположение детали относительно плоскости проекций: а — правильное расположение;
б — неправильное расположение; в — процесс и результат проецирования
Выберем для получения изображения вертикальную (фронтальную) плоскость проекций (К). Перед ней мысленно расположим деталь «Уголок» (рис. 2, в) так, чтобы формообразующая грань стала параллельно плоскости проекций. В результате прямоугольного (ортогонального) проецирования получим изображение детали, на котором грани предмета, параллельные плоскости проекций, отобразятся в натуральную величину. Боковые грани, перпендикулярные плоскости проекций, спроецируются в отрезки прямых. Ребра, параллельные фронтальной плоскости проекций, изобразятся в натуральную величину, а ребра, перпендикулярные ей, в точки.
Цилиндрические отверстия «Уголка» спроецируются в виде окружностей. Полученное изображение называется фронтальной проекцией. Эта проекция содержит основную информацию о форме детали, воспроизводит ее контур, дает представление о высоте и длине, не передавая при этом толщину или ширину.
 2015-10-22
2015-10-22 24696
24696
